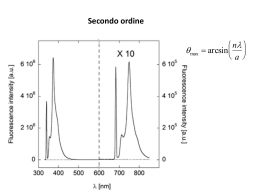
3
Proprietà della fluorescenza
Conseguenze: Regola di Kasha
• Lo spettro di emissione è
indipendente dalla lunghezza
d’onda di eccitazione
L’emissione avviene sempre dal livello vibrazionale
fondamentale di S1 (fa eccezione l’azulene, che emette
da S2 per la grande differenza energetica tra S2 ed S1)
Conseguenze: Stokes’ shift
• La luce emessa ha
sempre energie minori
di quella assorbita.
Conseguenze:
Regola dell’immagine speculare
• Lo spettro di emissione
può essere l’immagine
speculare di quello di
assorbimento.
• Vale se le curve di energia
elettronica dello stato
eccitato e fondamentale
sono simili.
Mirror rule
Sodium 7-aminonapthalene-1,3-disulfonate (ANDA)
Mirror rule fails!
Tempo di vita dello stato eccitato
Eccitazione IMPULSATA (d di Dirac)
kr= costante di decadimento radiativo
kn.r.= costante di decadimento attraverso i processi non radiativi
[M*]= concentrazione di molecole nello stato eccitato
 
 
d M*
 (k r  k nr ) M *
dt
M 
   (k  k )dt
M 
 M  
  ( k  k
ln 
 M  


d M*
r
*
   (k  k ) dt



M 
 
M   e

M   M  e
M 
*
dM
t
*
*
r
M* 0
nr
*
( kr  knr )t
*
0
*
*
0
nr
r
nr )t
0
*
*
0
( kr  knr )t
Tempo di vita dello stato eccitato
M   M  e
*
*
0
M   M  e 
( kr  knr )t
*

*
t
0
 
I  kr M *
 F  ns
I  I 0e

t
1

k r  k nr

 P  ms  min.
1
0
0
N/N o I/I
0
0
N/N o I/I
=10 ns
1
=10 ns
0.5
0.1
0.01
0
0
10
20
30
Time (ns)
40
50
0
10
20
30
Time (ns)
40
50
Resa quantica di un processo di
rilassamento
k
j 
decadimenti tramite il processo j
 j
totale decadimenti
 ki
 j  1
0   j 1
i
j
Resa quantica di fluorescenza
F 
decadimenti radiativi
kr

totale decadimenti
kr  knr
F 
fotoni emessi
fotoni assorbiti
Sperimentalmente, per molecole organiche, si trova
105 s 1  kr  109 s 1
105 s 1  knr  1011 s 1
kr
F 
kr  knr
kr 
F
1
F 
kr  knr
knr 
F
1
F
 kr 
1
F
 F  kr F

F
F

1
1   F 
F
1,1‘-dietil-2,2’-cianina
Chem. Phys Lett. 1986 130: 426.
0.6
10
11
k
T=84 K
r
0.4
10
nr
-1
k (s )
Resa quantica
k
10
9
0.2
10
T=298 K
0
0
0.5
8
10
1
 (ns)
1.5
2
100
150
200
T (K)
250
300
•Minore probabilità di transizioni radiative
•Maggiore probabilità di conversione intersistema
Rigidità e resa quantica
•Processi non radiativi inibiti
•Geometria di S0 ed S1 simile elevati fattori FC
4
Fluorescenza in stato
stazionario
Il fluorimetro
Beam splitter
Lampada
lecc.
Monocromatore
di eccitazione
Lente
Campione
lem.
Lente
Monocromatore
di emissione
Computer
PMT
“riferimento”
PMT
“segnale”
M+hn
Condizioni fotostazionarie
k
d M 
M+hn’
k
 k M   (k  k )M   0
M*
dt
k
M
k M   (k  k )M 
M   k  k 
A
*
r
*
A
r
nr
nr
*
A
st
*
st
M st
r
nr
A
(k r  k nr )
st
A
 
I st  k r M * st  k r k A M st  cost.
I st  k r  
•Si raggiunge (in pochi ns) una condizione di equilibrio, in cui è eccitata una frazione costante di
fluorofori.
•L’intensità di fluorescenza è costante e proporzionale alla resa quantica.
•Con le normali intensità delle lampade, questa frazione è sempre prossima a 0 (kA dipende dal
flusso di fotoni)