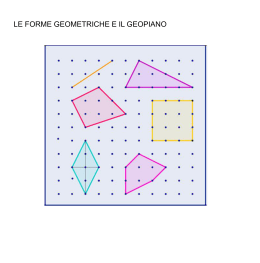
Giulia Zanelli Quarantini
Matelsup 2009-10
Intervista immaginaria a un
genio della Matematica
del passato:
CALEB
GATTEGNO
Come i bambini usano la
propria mente
D. Ci racconti della sua vita da
ragazzo, piuttosto particolare
CG: sono nato ad Alessandria, in
Egitto. La mia era una famiglia di
ebrei sefarditi, in casa si parlavano
correntemente Francese, Spagnolo,
Italiano e Inglese e, con il cuoco o lo
shoeshine, anche un poco di Arabo.
Vivevamo una realtà semicoloniale,
Alessandria era una città
assolutamente cosmopolita, che
accoglieva, nelle sue strade eleganti
e sulla splendida Corniche sul mare,
popoli, culture, lingue e religioni
molto diverse.
Con i miei cugini, frequentavamo le scuole italiane, inglesi o il Lycée Francais.
Per studiare, però, siamo quasi tutti andati in Europa. Lì a Basilea, in Svizzera,
nel 1937, ho portato a termine un dottorato di ricerca in Matematica.
D. Quello che colpisce, della sua vita e carriera, è la assoluta libertà
nell'individuazione del campo di indagine: nei suoi quasi 250 libri e oltre 500
articoli, si occupa via via di Matematica, di Psicologia, di Filosofia e spesso di
argomenti più generali, quali il cervello, l'amore, la consapevolezza ...
CG: il mio interesse principale è sempre stato la mente umana, la sua capacità
di apprendimento, che cosa influenza questa capacita di apprendimento,
compreso per esempio il ruolo importante che svolge l'affettività.
In particolare con i bambini ho cercato di pormi la domanda “Come funzionano?
Come usano la loro mente?”
Tutti i fondamenti della Matematica, come li conosciamo dalla
letteratura scientifica, sono basati su dogmi che secondo me
sono sbagliati: essi non lavorano sulla realtà della mente di chi
impara. Questo non è mai interessato, interessava solo scrivere
un elenco di passaggi per usare i meccanismi e ottenere i
risultati inseriti nei nostri programmi. Hanno così poco a cuore
la realtà, che non si sono resi conto che contare è un'attività
complessa.
Per secoli abbiamo insegnato che
contare è la base dell'aritmetica
elementare. Ciò è sbagliato:
avrete tutti notato che ci vuole un
po' prima che I ragazzi imparino
a dire 1, 2, 3, 4, in ordine, loro
dicono 1, 3, 7, 4 .. non è vero? E
quando finalmente imparano a
dire 1, 2, 3, noi siamo contenti,
ma non ci chiediamo perchè
all'inizio non ci riescono?
I bambini devono avere un po' di
tempo per capire le cose da soli.
http://www.atm.org.uk/about/peo
ple/gattegnoclips/ATMGattegno-07.mp3
D. Qual'è secondo lei il contributo più
importante che la sua opera ha fornito
all'insegnamento della Matematica ai
bambini?
CG:si tratta di una forma di disciplina che
gli insegananti devono dare a sé stessi,
parlo dell'educazione degli insegnanti.
Essi devono realizzare che la realtà
deve essere presentata agli altri
partendo dal modo in cui essi hanno
ragionato, non da come essa è stata
tramandata: quindi, se io sono in
possesso di alcuni criteri, per esempio
per addizionare due frazioni, il mio
lavoro consiste nel fare in modo che
anche gli studenti abbiano dei criteri,
non la Conoscienza. La Conoscienza
scaturirà da essi.
Per esempio: una volta, alla mia scrivania ad Addis Abeba nel 1957, mi sono
sorpreso ad arrossire, mi vergognavo di me stesso. Venti anni dopo il mio
dottorato in Matematica, ho capito che addizionare due frazioni significa fare
un'addizione. Ovviamente, lo dicevo sempre, lo sapevo fare, sapevo trovare le
soluzioni, ma non avevo capito. Improvvisamente mi è stato chiaro che ogni
volta che io sommo 2 mele e 3 pere, non ho 5 mele o 5 pere. Ho qualcosa che è
cambiato, ho 5 frutti. Per capire come metterle insieme , dovevo passare ad un
altro livello, dove la “melitudine” e la “peritudine” vengono rimpiazzate dalla
“fruttitudine”. Solo allora io posso dire 5.
E non avevo mai capito che Denominatore Comune vuol dire dare a entrambe lo
stesso nome. Ora, al centro della parola Denominatore vedo la parola Francese
nom, che conoscevo benissimo. Non mi era mai parso così chiaro che è
l'addizione che costringe a trovare il denominatore comune, non la frazione.
Ecco perché mi vergognavo.
http://www.atm.org.uk/about/people/gattegnoclips/ATM-Gattegno-01.mp3
D: lei pensa quindi che il metodo di insegnamento tradizionale possa essere
stato in qualche maniera poco efficace?
CG: mi sento dire spesso “Io insegno, ma loro non imparano”. Be', se lo sai,
smetti di insegnare ...! Non intendo dire che ti devi licenziare, ma smettere di
insegnare in una maniera che non riesce a fare imparare. Cerca di capire che
cosa devi fare per essere ogni giorno più preparato per aiutare i giovani a
corredare le proprie menti con cose che sono così elementari che quello che
normalmente viene insegnato in 5 anni, io lo posso insegnare in 18 mesi.
Mia figlia ha imparato a leggere a 20 mesi e mio figlio a tre anni, non perché
glielo abbia insegnato io, ma perché ho lasciato che imparassero.
http://www.atm.org.uk/about/people/gattegnoclips/ATM-Gattegno-06.mp3

D: oltre ai famosi regoli CusineaireGattegno, lei ha inventato molti altri
strumenti per una pedagogia del
fare e del costruire.

CG: Si, per sempio i “geopiani”: si
tratta di strumenti didattici adatti a
favorire l’esperienza geometrica:
sono efficaci a diversi livelli di
apprendimento.Su di una tavoletta
di legno è disegnato un reticolato i
cui nodi sono messi in evidenza con
dei chiodini o delle viti; fra di essi si
possono tendere degli elastici di
diverso colore. Sui geopiani si
possono tracciare le più diverse
figure;

diviene così possibile
rappresentare e studiare numerose
differenti situazioni geometriche:
relative alla forma e alle proprietà
delle figure, alle dimensioni ed
estensioni, problemi di simmetria, di
similitudine, di ricerca di casi
possibili, di classificazione ed altri
ancora. Con un geopiano a 9 chiodi
si possono ottenere tutti i tipi di
quadrilateri: quadrati, rombi,
rettangoli, parallelogrammi, trapezi,
deltoidi, ecc.


Con un geopiano a 16 chiodi si può
illustrare il teorema di Pitagora
generalizzato o teorema di Carnot.
Con un geopiano a 25 chiodi si
possono costruire molti angoli
oppure introdurre i primi concetti sul
piano cartesiano o proporre esercizi
sulla simmetria assiale e su quella
centrale o sulla determinazione
dell’area di figure poligonali.
Naturalmente aumentando il
numero dei chiodi del geopiano,
aumentano anche le situazioni che
si possono proporre.
E’ evidente che un geopiano con 121 chiodi potrà essere utilizzato
magnificamente per introdurre il piano cartesiano o per l’equivalenza delle figure
poligonali e per metterne in evidenza i vari elementi. Un altro geopiano è quello
formato da un reticolato a forma didodecagono regolare (i 12 chiodi sono disposti
su una circonferenza) e permette di rappresentare triangoli equilateri, quadrati,
esagoni e dodecagoni. Questo geopiano permette pure di delimitare archi, settori,
individuare diametri, corde, rappresentare angoli al centro, angoli alla
circonferenza, stabilire proprietà di archi e corde, dimostrare la relazione
esistente fra angoli inscritti nella circonferenza e i corrispondenti angoli al centro.
Delle innumerevoli attività che si possono
effettuare con questi strumenti è bene tenere presente l’opportunità che gli allievi
riproducano sul quaderno le situazioni e i risultati realizzati sul geopiano.


D: lingua 2. dopo aver fondato la
Cuisenaire Company in Inghilterra nel
1954, della quale è stato direttore fino
al 1986, è stato in Etiopia, in qualità di
membro della commissione che si
propone di trovare una soluzione al
problema dell'analfabetismo.
CG: si, ed è in quella occasione che ho
sviluppato un metodo pensato per
rendere più semplice l'alfabetizzazione,
che in seguito è stato utilizzato
moltocome strumento per
l'insegnamento dell'Inglese come lingua
2

E' stato chiamato “words in
colour”: codifica per colore
i fonemi e rende quindi più
intuitivo l'approccio alla
lingua.
D: Dal 1966, lei ha lavorato a
New York
CG: ho diretto “Schools for the
Future” un'organizzazione
di ricerca benefica e mi
sono occupato di
“Educational Solutions”,
che pubblica materiale per
l'insegnamento e si occupa
della formazione degli
insegnanti.
http://www.educationalsolutio
ns.com/
August 4, 1988
Caleb Gattegno, 76, a Proponent Of Novel Learning Theories, Dies
By GLENN FOWLER
Caleb Gattegno muore a Parigi nel 1988, in poco dopo aver partecipato ad
un ultimo seminario.
In occasione della sua morte John Holte, autore di “Perché i bambini
falliscono” ha affermato:” Gattegno è stato abile come pochi altri nel farci
capire chiaramente la natura dell'imparare non, come molti fanno,
spezzetandolo in tanti frammenti scollegati e poco reali, ma chiedendoci
qual'è la 2sensazione” dell'imparare”.
BIBLIOGRAFIA
Come abbiamo avuto modo di dire, la bibliografia di
Gattegno è monumentale, composta da monografie,
saggi su riviste, manuali che accompagnano i suoi
strumenti didattici. Anche gli argomenti spaziano dalla
didattica della Matematice, all'insegnamento delle
lingue, dalla Psicologia alla Filosofia, alla Pedagogia e
non solo
Per un tentativo di biblio grafia esaustiva, si rimanda al
bel sito di Educational Solutions:
http://educationalsolutions.com/index.php