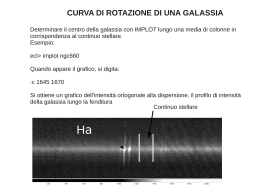
L’intensità della riga di emissione Ha nelle
galassie a spirale è un potente strumento
per esplorare il loro tasso di formazione stellare.
Esistono altri metodi per stimare la SFR nelle
galassie a spirale, tra cui l’utilizzo
dell’emissione infrarossa e UV.
Di questi metodi di misurazione, le osservazioni
in Ha sono le uniche che possono
essere effettuate con telescopi a terra.
• Galassia a spirale di tipo c
• Distanza di circa 17 Mpc
• Coordinate in cielo (all’equinozio
2000.0) A.R.=10h 42m 07.5g,
Dec=+13° 44’ 49’’
• Magnitudine apparente: m = 12,8
•Bias e flat-field
•Calibrazione delle lunghezze d’onda
•Calibrazione del flusso
•Sottrazione delle righe di cielo
Lo spettro presenta
•Una striscia centrale orizzontale più
luminosa, dovuta al nucleo della
galassia
•Righe spettrali lungo la fenditura,
corrispondenti a diverse regioni di
emissione della galassia
Zone dove la riga Ha è più brillante :
• N è il nucleo della galassia
• A1, A2, A3 e B2, B2, B3
Le righe di emissione: funzioni la cui area
rappresenta il flusso contenuto nella riga:
Iλ   I 0  e
Fλ 0  


λ  λ 0 2

 I0  e
2σ 2

 λ  λ 0 2
2σ 2
dλ

Dove I(l) è l’intensità della riga a diverse lunghezze d’onda, I0 è l’intensità
della riga al centro (l0), F(l0) è il flusso della riga e σ la sua larghezza.
Trovato i flussi di Ha e Hb si è calcolato i loro rapporti e
confrontati con il decremento di Balmer teorico per un gas
ionizzato a T = 10 000 K
I ( H ) / I ( H )  2,86
I ( H ) /( H )  0,47
I ( H ) /( H )  0,26
Purtroppo, di solito, Ha è ben visibile, mentre Hb è debole, talvolta
così debole da non essere misurabile.
• conversione del flusso di Ha in luminosità (L)
z
λ  λ0
λ0
• calcolo della distanza per mezzo della legge di Hubble
D
cz
H0
(Mpc)
• moltiplicazione del flusso per 4πD²
LHα   4π  D 2  FHα 
(erg/sec)
• per ottenere la star formation rate si usa la relazione:
SFR  7.9 10-42 LHα 
(M/anno)
Poiché la riga Hα viene emessa quando gli elettroni liberi si ricombinano con i
loro protoni, la sua intensità è strettamente legata al numero di fotoni
ionizzanti (cioè con energia > 13.6 eV) emessi da una sorgente, in questo caso
stelle calde:
Q ion  7.3 1011 LHα 
(fotoni/sec)
E conoscendo il numero tipico di fotoni ionizzanti emessi da una stella calda,
ad esempio una O5
Qion (O5)  5 10 49
(fotoni/sec)
si può stimare il numero di stelle di quel tipo spettrale che stanno
fotoionizzando il gas.
F(H)
F(Hα)
Hα/H
A(V)
A3
9,49×10-16
5,96×10-15
6,27
2,47
A2
5,70×10-16
4,64×10-15
8,14
3,28
A1
5,02×10-16
4,48×10-15
8,93
3,56
N
1,38×10-15
6,49×10-15
4,70
1,57
B1
8,14×10-16
6,81×10-15
8,37
3,37
B2
7,43×10-16
4,42×10-15
5,95
2,30
B3
1,13×10-15
6,21×10-15
5,51
2,06
A3
A2
A1
N
B1
B2
B3
I(Hα)
L(Hα)
SFR
Qion
N(O5)
3,83×10-14
1,69×1039
0,013
1,23×1051
24,7
5,49×10-14
2,42×1039
0,019
1,77×1051
35,3
6,54×10-14
2,88×1039
0,023
2,10×1051
42,0
2,11×10-14
0,93×1039
0,007
0,68×1051
13,6
8,62×10-14
3,80×1039
0,030
2,77×1051
55,5
2,50×10-14
1,10×1039
0,008
0,80×1051
16,1
2,93×10-14
1,29×1039
0,010
0.94×1051
18,8