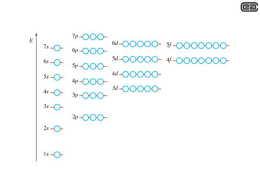
Magnetochimica
AA 2012-2013
Marco Ruzzi
Marina Brustolon
1. The coupling of Angular Momenta
2. EPR in a nutshell
3. The exchange spin Hamiltonian
4. The Zero Field Splitting spin Hamiltonian
5. Radicals with delocalized electron spin density
Magnetochimica
AA 2011-2012
Marco Ruzzi
Marina Brustolon
The coupling of Angular Momenta
The coupling of angular momenta 1
Two non interacting particles, each with a constant
angular momentum, are characterized each by its
own eigenvalues of the operators magnitude of the
vectors and component along z.
Jˆ12
Ĵ 2
2
Jˆ z1
Jˆ z 2
with eigenvalues
with eigenvalues
j1 ( j1  1) 2
j2 ( j2  1) 2
m j1 
m j 2
The wavefunctions of the two particles can be referred to these
quantum numbers, therefore:
j1 , m J1
j 2 , m j2
or, considering the two particles together
j1 , j 2 , m J1 , m J 2
The coupling of angular momenta 2
• There are
(2 j1  1)(2 j2  1)
states
j1 , j 2 , m J1 , m J 2
For example, if the two momenta are two spin ½, there are 2x2 =4
states:
1111
1 111
 1 2 , 
 1 2 ,
2222
2 222
111 1
1 11 1

 1  2 , 

 1 2
222 2
2 22 2
We can use a shorter notation, as J1 and J2 are always 1/2:
j1 , j 2 , m J1 , m J 2  m J1 , m J 2
The coupling of angular momenta 3
For the orbital momenta of two p electrons, J1 = J2 =1 , therefore
(2 J1  1)  (2 J 2  1)  3  3  9
states
mJ1 mJ 2
11 , 10 , 01 , 00 , 1 1 , 11 , 10 , 0 1 , 1 1
Each of these states is an eigenstate of Jz1 and Jz2. Moreover, they are
eigenstates of
Jˆ z  Jˆ z1  Jˆ z2
with eigenvalues
M J   ( m J1  m J 2 )
mJ1 mJ 2
The states
are eigenstates of Jz1, Jz2 and also of
Jz , as these three operators commute.
The coupling of angular momenta 4
m1 , m2
Mtot=
m1+m2
1,1
2
1,0
1
0,1
1
0,0
0
 1,1
0
1,1
0
 1,0
-1
0,1
-1
 1,1
-2
These states are eigenfunctions of the operators:
J 12
J 22
J z1
J z2
Jz
with quantum numbers
j1
j2
m1
m2
M tot
but they are not eigenfunctions of
J
as
2
tot
J2
 J  J 1  J 2 
2
2
does not commute with
J z1 J z 2
The coupling of angular momenta 5
So, we have two choices: either use the basis set of eigenfunctions of:
J 12
J 22
State
J z2
J z1
M =m1+m2
1,1
2
1,0
1
(and
J z ) : j1 , j2 , m1 , m2 , M
Uncoupled
basis
or find a basis set of eigenfunctions of:
J 12 J 22 J 2 J z
j1 , j 2 , J , M
Coupled
basis
0,1
1
0,0
0
 1,1
0
1. The dimensions of the basis sets are the same.
1,1
0
2. The values of J vary between
 1,0
0,1
-1
 1,1
-2
-1
j1+j2 , j1+j2-1,…, | j1+j2|
3. Each function of the coupled basis with a value
Mk is a linear combination of the functions of the
uncoupled basis with the same Mk value.
The coupling of angular momenta 6
Therefore if j1=1 and j2=1, the possible J values are:
J = 2 ,1, 0
For each J value there are 2J+1 states, with MJ = J, J-1,…,-J
State
M
=m1+m2
For J = 2 we have
five functions::
j1 , j 2 , J , M
1,1
2
1,0
1
1,1,2,2
0,1
1
1,1,2,1
0,0
0
 1,1
0
1,1,2,0
1,1
0
1,1,2,1
 1,0
0,1
-1
 1,1
-2
-1
1,1,2,2
The two functions in orange
can give two independent
linear combinations: one of
the two is this coupled
function.
The two functions in blue
can give two independent
linear combinations: one of
the two is this coupled
function.
The coupling of angular momenta 7
J = 2 ,1, 0
For J = 1 there are 3 states, with MJ = 1, 0, -1
State
M
=m1+m2
For J = 1 we have
three functions::
j1 , j 2 , J , M
1,0
1
0,1
1
0,0
0
 1,1
0
1,1,1,0
1,1
0
1,1,1,1
 1,0
0,1
-1
-1
1,1,1,1
The other linear combination
is this coupled function.
The other linear combination
is this coupled function.
The coupling of angular momenta 8
J = 2 ,1, 0
For J = 0 there is 1 state, with MJ = 0
State
M
=m1+m2
0,0
0
 1,1
0
1,1
0
For J = 0 we have
one function:
j1 , j 2 , J , M
1,1,0,0
These three functions can
give three independent
linear combinations: this
one, and the others
indicated in the previous two
slides.
The coupling of angular momenta 9
The coefficients of the linear combinations of the uncoupled basis
to give the coupled one are the Clebsch-Gordan coefficients:
j1 , j 2 , J , M 
 C( j , j
1
2
, J , m1 , m2 ) j1 , j 2 , m1 , m2
m1m2
with M =m1+m2
The C-G coefficients can be obtained with recursion formulae, or can
be found in tables.
Tables of Clebsch-Gordan
coefficients
M
For two spins =1/2
Jtot=
Valore di Jtot
Base disaccoppiata
Coefficiente della
combinazione lineare
Jtot=
Coefficienti del
tripletto
Base disaccoppiata
Coefficienti del
singoletto
Two spin =1/2, uncoupled basis:
j1 , j2 , mJ1 , mJ 2
1111
1 111
 1 2 , 
 1 2 ,
2222
2 222
111 1
1 11 1

 1  2 , 

 1 2
222 2
2 22 2
Coupled basis, following the Clebsch-Gordan table:
j1 , j2 , J , M
1 1
1 1 1 1
, ,1,1  , , ,
2 2
2 2 2 2

Triplet, J=1, M=1
1 1
1  1 1 1 1
1 1 1 1 
, , 0, 0 
,
,

,


, ,  ,   Singlet, J=0,M=0

2 2
2 2 2 2 
2 2 2 2 2
1
   

etc.
2
I due momenti sono disaccoppiati, cioè
ciascuno può essere sul suo cono di
precessione in qualunque posizione
indipendentemente dall’altro.
Due momenti angolari disaccoppiati
La somma delle loro
proiezioni sull’asse z è
sempre definita
Due momenti angolari accoppiati
I due momenti sono accoppiati, e la loro
somma vettoriale dà il momento totale J.
Ciò significa che non sono in una posizione
qualsiasi uno rispetto all’altro, ma sono
accoppiati in modo da dare sempre come
somma vettoriale J.
Si noti inoltre che negli stati nei quali è
definito J, restano definiti j1 e j2, ma non
sono più definiti m1 e m2, ma solo la loro
somma M .
S=1
MS=+1
S=1
s2
s2
s2
s1

s1
MS=-1

S=0
MS=0
s2
1
MS=0
1
2
S=1
  
s1
Rappresentazione
vettoriale dello
stato di tripletto
2
s1
  
Rappresentazione
vettoriale dello
stato di singoletto
Using the raising and lowering spin operators 1
We know that the eigenfunctions of angular momentum operators
J2 and Jz are characterized by quantum numbers J and M.
For each J value we have a family of functions with different
values of M:
j1 , j 2 , J , M J
with
M J  J , J  1,..., J
The effect of the so called
raising and lowering operators:
j1 , j 2 , J , J
j1 , j 2 , J , J  1
J   J x  iJ y
j1 , j 2 , J , J  2
J   J x  iJ y
........
J
J
is to transform a function with MJ
respectively to the one with MJ+1
and MJ-1
Using the raising and lowering spin operators 2
The effects of raising and lowering operators on a function
characterized by J and MJ are the following (see note*):
I  I , m I  ( I ( I  1)  m I (m I  1)) 1 2  I , m I  1
I  I , m I  ( I ( I  1)  m I (m I  1)) 1 2  I , m I  1
For example let us consider the simple pair of spin functions  and :
I   I
1 1
2 2
 (1 / 2  (3 / 2)  1 / 2  3 / 2))1 2  0
I   I
1 1
2 2
 (1 / 2  (3 / 2)  1 / 2  1 / 2))1 2  I , mI  1  
Therefore:
I- = 
I+  = 0
I-  = 0
I+  = 
*We use here different symbols: I instead of J, mI instead of MJ
Exercise:
Obtain the spin functions of the coupled basis from an
uncoupled basis for two electron spins (or any other
angular momentum with J=1/2), by using the raising
and lowering operators.
So, which basis of eigenfunctions for two or
more angular momenta should be used?
Coupled or uncoupled?
The answer stays in the type of spin
Hamiltonian, as we will see.
Nel sito WEB della Stanford University con
questo indirizzo trovate una utile serie di
slides sui momenti angolari:
• http://www.google.it/url?sa=t&rct=j&q=&esrc=s&
source=web&cd=2&ved=0CCwQFjAB&url=http
%3A%2F%2Fwww.stanford.edu%2Fgroup%2Ff
ayer%2Flectures%2FChapter1508.ppt&ei=zK5yULLyEaLg4QS2iID4Cw&usg=AF
QjCNEqloSuvqmXYnMWOidt3G-_Wwj4Ag