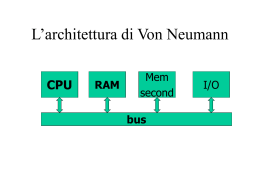
Informatica di base
A.A. 2002/2003
Docente: Prof. Francesca Rossi
E-mail: [email protected]
Tel: 049-8275982
Studio: Via Belzoni 7, primo piano
1
Organizzazione del corso
24 ore di lezione (3 crediti) in aula LUM 250
 prime tre settimane:
Lunedi’- Martedi’ – Mercoledi’ 11:20-13:00
altre settimane (dal 21 Ottobre):
Martedi’ 11:20-13:00
 16 ore di laboratorio (2 crediti) in aula
laboratorio
 dopo le prime tre settimane
 tre gruppi di studenti
 Mercoledi’ 14-16 e 16-18, Giovedi’ 14-16
 iscrizione in terminali per login password
(tra qualche giorno)
2
Materiale ed esame
Dispensa disponibile alla Libreria Progetto (Via
Marzolo 28, Via Portello 5/7)
Sito web del corso (pronto tra pochi giorni)
Esame con domande a scelta multipla
3
Sommario degli argomenti – parte 1
I circuiti logici
Il sistema binario
L’architettura di Von Neumann
Interi, reali e caratteri in un computer
Linguaggio macchina ed Assembler
4
Sommario degli argomenti – parte 2
Sistemi operativi: DOS, Unix/Linux,Windows
Word processors: Word
Fogli elettronici: Excel
Sistemi per la gestione di basi di dati
Reti: TCP/IP, Internet, ftp, telnet, posta
elettronica
WWW: http, Netscape, HTML, motori di ricerca
5
Hardware
L’ Hardware di un computer
un computer è ottenuto assemblando un gran
numero di componenti elettronici molto semplici
3 tipi di componenti fondamentali:
A
A
R
B
R
A
R
B
A B
R
A B
R
A
R
0 0
0
0 0
0
0
1
0 1
0
0 1
1
1
0
1 0
0
1 0
1
1 1
1
1 1
1
6
AND
A
B
OR
A AND B
A
B
NOT
A OR B
A
NOT A
falso falso
falso
falso falso
falso
falso
vero
falso vero
falso
falso vero
vero
vero
falso
vero
falso
falso
vero
falso
vero
vero
vero
vero
vero
vero
vero
A B
R
A B
R
A
R
0 0
0
0 0
0
0
1
0 1
0
0 1
1
1
0
1 0
0
1 0
1
1 1
1
1 1
1
A
A
R
B
R
B
A
R
Completezza di and, or, e not
16 operazioni logiche binarie (tante
quante possibili scelte di 4 valori)
4 operazioni logiche unarie
Tutte possono essere ottenute
componendo and, or, e not
8

A
A  B
B
A B A  B
falso falso
vero
0 0
1
falso vero
vero
0 1
1
vero
falso
falso
1 0
0
vero
vero
vero
1 1
1
A  B equivale a (NOT A) OR B
A B NOT A
0 0
1
(NOT A) OR B
1
0 1
1
1
1 0
0
0
1 1
0
1
A
R
B

A B
A  B
0 0
1
0 1
0
1 0
0
1 1
1
A  B equivale a
(A  B) AND (B  A)
A B A  B B  A (A  B)AND(B  A)
0 0
1
1
1
0 1
1
0
0
1 0
0
1
0
1 1
1
1
1
A
B
R
 o XOR
A XOR B equivale a
NOT (A  B)
A B
A  B
0 0
0
0 1
1
A B
A  B
NOT(A  B)
1 0
1
0 0
1
0
1 1
0
0 1
0
1
1 0
0
1
1 1
1
0
A
B
A
R
B
X R
Siccome (un rettangolo è un quadrato se ha altezza
uguale alla base), allora [se un rettangolo (non è un
quadrato) esso (non ha altezza uguale alla base)].
A = (B  A)  [(NOT A)  (NOT B)]
A B B  A NOT A
NOT B
(NOT A)  (NOT B)
A
0 0
1
1
1
1
1
0 1
0
1
0
0
1
1 0
1
0
1
1
1
1 1
1
0
0
1
1
Il risultato è sempre 1, ossia sempre vero.
L’asserzione è una tautologia (o un teorema).
Dalla tabella di verita’ ad un
circuito
Tanti input quante sono le dimensioni
della tabella
Un solo output
Un or all’output
Tanti and quanti sono gli 1 della tabella
Input degli and: 1 se diretto, 0 se negato
A B
A  B
A
0 0
0
B
0 1
1
1 0
1
1 1
0
R
13
Nand e nor
Non servono tre operazioni (and, or, not)
Basta una tra :
nand (not and) e nor (not or)
14
NAND
A
B
A NAND B
NOR
A
B
A NOR B
falso falso
vero
falso falso
vero
falso vero
vero
falso vero
falso
vero
falso
vero
vero
falso
falso
vero
vero
falso
vero
vero
falso
A B
R
A B
R
0 0
1
0 0
1
0 1
1
0 1
0
1 0
1
1 0
0
1 1
0
1 1
0
A
A
R
B
R
B
NOT
AND
A
A
R
R
B
OR
A
R
B
Memorie
Processore = griglia di milioni di porte
logiche
Frequenza (con cui riceve l’input)
Esempio: 2 Giga Hertz (2 miliardi di cicli al
secondo)
Input ad un ciclo  output al ciclo
successivo
17
Rappresentazione binaria
Base 10  cifre da 0 a 9
Base 2  cifre 0 e 1
Sequenza di cifre decimali
dk d k-1 … d1 d0
 numero intero
dk x 10k + dk-1 x 10 k-1 + … d1 x 10 + d0
 Esempio: 101 in base 10 e’ 1x100+0x10+1x1
18
Circuiti aritmetici
Rappresentazione binaria di un intero:
01011012 = 1·25 + 1·23 + 1·22 + 1·20
= 32 + 8 + 4 + 1
= 4510
 Valore minimo di una sequenza di n
cifre binarie: 000 … 0 (n volte) = 010
 Valore massimo: 1111…111 (n volte) =
2n-1 + 2 n-2 + … + 22 + 21 + 20 + 1 = 2n –1
Esempio: 111 = 22 + 2 + 1 = 7 = 23 -1
Una proprietà dei numeri binari
1001001= 73
100100 = 36 = 73/2 e questo è il resto
Eliminare il bit più a destra corrisponde a
dividere per 2 il valore, ed il bit eliminato è il
resto
20
Trasformazione di un numero in base 10
a binario
125
125/2=62
62/2=31
31/2=15
15/2=7
7/2=3
3/2=1
1/2=0
resto 1
resto 0
resto 1
resto 1
resto 1
resto 1
resto 1
125 in binario è
1111101
rappresenta 62
rappresenta 31
etc
21
Circuiti aritmetici
Somma:
 Colonna per colonna, da destra a sinistra
 Riporto se la somma su una colonna supera
la base
 Tre cifre binarie (prima riga, seconda riga,
riporto), somma =1 se una o tre sono 1,
riporto = 1 se almeno due sono 1
Riporto:
1 1 1 1 0 0
0111002 +
1001112 =
----------10000112
Somma binaria
1
11
riporti
1010011+
1100011=
----------10110110
Si vuole costruire un circuito per
sommare due numeri binari
Iniziamo con un circuito che faccia la
somma su di una colonna
23
Vogliamo un circuito che con input due bit
corrispondenti ed il riporto precedente
calcola la loro somma ed il nuovo riporto.
x
y
R
ADD
R'
S
La somma S è 1 se tutti e tre i bit in input
sono 1 oppure solo uno di essi è 1.
Questo si esprime con la formula logica:
S = {[(X AND Y) AND R] OR
[X AND (Y NOR R)]} OR
{[Y AND (X NOR R)] OR
[R AND (X NOR Y)]}
Il nuovo riporto R' è 1 se almeno due bit in
input sono 1.
Questo si esprime con la formula logica:
R' = [(X AND Y) OR (X AND R)] OR
(Y AND R)
2 bit da sommare
riporto per
la prossima
colonna
2 output
3 input
riporto
1-ADD
risultato su questa
colonna
27
Tabelle di verità
bit da sommare
riporto
0
1
0
1
00
01
0
1
1
0
00
01
0
0
0
1
10 11
1
0
0
1
risultato
10 11
0
1
1
1
riporto
28
Dalle tabelle di verità sappiamo come
costruire il circuito:
1-ADD
riporto
risultato
Somma di numeri di 4 bits
Riporto
finale
1-add
1-add
1-add
1-add
0 riporto
iniziale
risultato
30
Componendo 6 circuiti ADD si ottiene il
circuito
x5
y5
x4
y4
ADD
R
s5
x3
y3
ADD
R
s4
x2
y2
ADD
R
s3
x1
y1
ADD
R
s2
x0
y0
ADD
R
s1
0
ADD
R
s0
Che calcola la somma di due numeri di 6 bit
31
Memoria (volatile)
bit
A
X
flip
output
B
reset
ciclo
reset
flip
A B output
ciclo
reset
flip
0
0
0
?
?
1
0
0
?
2
1
0
3
1
4
A B output
?
7
0
1
0
1
0
1
?
8
0
1
1
1
0
?
1
?
9
0
0
1
1
1
0
?
0
?
10
0
0
1
1
1
0
0
?
0
0
11
0
0
1
1
1
5
0
0
0
1
0
12
0
0
1
1
1
6
0
0
0
1
0
13
0
0
1
1
1
bit
A
X
flip
output
B
reset
ciclo
reset
flip
A
B
output
14
0
1
1
1
1
15
0
1
0
1
1
16
0
0
0
1
0
17
0
0
0
1
0
18
0
0
0
1
0
19
0
0
0
1
0
20
0
0
0
1
0
Ricevimento e sito corso
www.math.unip.it/~frossi/info-base.html
Orario di ricevimento: Mercoledi’ 16:3018:30 nel mio studio (o in un’aula)
34
Esercizio
•Determinare la tavola di verità del
seguente circuito:
A
è una tavola
or
not
nota?
B
not
and
R
or
35
Esercizio
•Partendo dalla tavola di verità
dell’esercizio precedente, costruite un
circuito che la realizza seguendo il
metodo di costruzione generale visto in
classe.
36
Esercizio
•Si disegni un circuito logico che realizza
la seguente tavola di verita’:
•A=0, B=0  R = 1
•A=0, B=1  R = 1
•A=1,B=0  R = 1
•A=1, B=1  R = 0
37
Esercizio
•Dare la tavola di verita’ delle formule:
•(A  NOT(B)) OR (A AND B)
•A OR (A AND NOT(B))
•(NOT(A)  NOT(B)) OR (NOT(A)
AND B)
38
Esercizio
•Scrivere la rappresentazione binaria dei
numeri decimali:
•30
•36
•15
39
Esercizio
•Scrivere la rappresentazione decimale
dei numeri binari:
•1000
•1010
•01011
•10111
40
Iscrizione per l’accesso al
laboratorio
Sito per le iscrizioni:
http://iscrizioni.math.unipd.it
Dopo tre giorni: ritirare login e password
e firmare
Da casa o da due terminali nell’androne
del laboratorio
41
L’architettura di Von Neumann
CPU
RAM
Mem
second
I/O
bus
42
RAM= Random Access Memory
memoria ad accesso casuale
Nella RAM, come ovunque in un computer, le
informazioni sono sempre rappresentate con
sequenze di 0 e di 1. Numeri binari.
La RAM quindi è fatta per contenere tali
numeri.
un bit può contenere o 0 o 1
un byte è una sequenza di 8 bits
una parola consiste di 4 bytes
43
bit
quindi la RAM è
una sequenza di bytes
da cui si leggono ed in
cui si scrivono singoli
byte o blocchi di 4
bytes consecutivi: le
parole.
byte
parola
Indirizzamento di byte e parole
0
0
1
2
3
000000
000000
000000
000000
00
01
10
11
1
4
5
6
7
000001
000001
000001
000001
00
01
10
11
2
8
9
10
11
000010
000010
000010
000010
00
01
10
11
Unità di misura della RAM
1 K bytes circa 1.000 bytes
210=1024
1 Mega byte circa 1.000.000 bytes
1 Giga byte circa 1.000.000.000 bytes
220
230
1 Tera byte circa 1.000.000.000.000 bytes
240
46
PROPRIETA’ della RAM
RAM => accedere ad ogni byte ha la stessa
durata (10**-7 sec): non dipende da quale
byte è stato acceduto prima
è volatile: se tolgo la spina l’informazione è
persa (c’è anche la ROM)
ogni byte ha un indirizzo 0,1,2......
il byte e’ la minima quantita’ accessibile
(attraverso il suo indirizzo)
47
La CPU: unità centrale di calcolo:
esegue programmi che sono nella RAM
bus
P
CPU
IP
ALU
RC
•R0
Cis1 Cis2
RAM
Cisk
registri di calcolo
•Rn
48
La CPU esegue continuamente il ciclo
ADE=Access/Decode/Execute
Access: preleva dalla RAM la prossima
istruzione da eseguire (l’indirizzo è in P,
l’istruzione viene messa in IP)
Decode: capisce che istruzione c’è in IP: isi
Execute: la esegue mediante il circuito Cisi
1 ciclo= 10**-9 sec
49
Memoria Secondaria
 è permanente
dischi fissi, floppy, nastri magnetici, CD
accesso sequenziale (il tempo varia a
seconda dell’accesso precedente)
è adatta per leggere/scrivere grandi
quantita’ di dati (in posizioni contigue)
50
I/O=Input/Output
Dispositivi di comunicazione utente
computer. In un computer moderno:
input=tastiera
output=video / stampanti
velocita’ diverse e molto minori delle
altre parti del computer (decimi di
sec)
51
Componenti di un PC
I componenti del calcolatore si dividono in due
categorie:
Hardware (parte fisica, meccanica, elettronica)
Software (istruzioni e comandi)
Unità di misura:
Velocità
Memoria
MHz Milioni di operazioni al secondo
Byte, KB, MB, GB, TB
52
Macchina Hardware e Macchina
Software
applicativi
sistema operativo
macchina
hardware
Agli albori dell'informatica, l’utente programmava in
binario (Ling.Mac.) scrivendo i programmi nella RAM
traduce per noi in
linguaggio macchina
software
utente
macchina
hardware
La macchina software permette:
•input/output facile
•programmazione in linguaggi ad alto
livello, come Java (parte III)
•rende disponibili programmi per
compiere operazioni molto complicate
(applicativi) (parte II)
Tutto viene comunque "fatto" dalla
macchina hardware!!
INTERI REALI e CARATTERI
Il computer ha memoria finita e
quindi l’insieme dei numeri interi e
reali che sono rappresentabili è
necessariamente finito!
56
Rappresentazione binaria
Numero binario: b
bi=1 o 0
n-1
b
n-2
… b 0, dove
Corrisponde al numero decimale
(b n-1 x 2 n-1) + (b n-2 x 2 n-2) +… + (b 0 x 2 0)
Esempio: 101 corrisponde a 1x4+0x2+1x1 = 5
Esempio: 11 = 1x2 + 1x1 = 3
57
Gli interi nel computer
Generalmente gli interi occupano
4 bytes = 32 bit
Con n bit, si rappresentano
interi positivi da 0 a 2n –1
 0 = n zeri
 2 n-1 = n uni,
cioe’ 1x2 n + 1x 2 n-1 = … + 1x2
e i negativi ?
0
58
Prima rappresentazione
Il bit n rappresenta il segno:
0 = positivo 1 = negativo
PROBLEMI:
2 zeri (+0 e -0)
operazioni complicate
59
Seconda rappresentazione
Usare la rappresentazione in
complemento a 2:
• positivi da 0 a 2n-1 -1 lasciando a 0 il bit
n
•negativi da -2 n-1 a -1 si rappresentano
come il complemento a 2 del valore
assoluto
60
Esempio, con
n=6
0, 1,…….31, 32, ……, 63
positivi
negativi
-32............-1
32  32-64= -32
33  33-64= -31 ………..
63  63-64= -1
61
Esempio:
Supponiamo n=6
-4 viene rappresentato come
complemento a 2 di 000100 (= 4)
cioè 111011+1=111100 = 60 (10)
si calcola anche: -4 + 26 = 60
62
Complementando 0 si ottiene ancora 0
64in binario
0=
--64 ha gli ultimi 6 bit uguali a 0
1000000000000=
------1000000
Complementando 32 si ottiene
64in binario
32=
--32 ha il bit 5 uguale a 1(negativo)
1000000100000=
------0100000
In generale: con n bits

positivi
0 ….. 2n-1-1
negativi -2n-1 …... -1
64
La somma è semplice
n=6
Somma di numeri positivi 10+12
10+
12=
--22
in binario
001010+
001100=
------0010110
65
Altro esempio con n=6
Vogliamo:
10 - 32
-32
-32+64 = 32
10 + 32 = 42 che rappresenta un
numero negativo (è >31)
che numero ?
42 - 64 = -22 OK
71
-3-22
n=6
-3 -> 61= 111101
-22 -> 42 = 101010
1 100111=
64
+ 39
Basta buttare via l’1 in colonna 7
39 - 64 = -25 come desiderato
72
Non sempre la somma va bene:
25+10= 35
TROPPO GRANDE !!
che con 6 bit rappresenta un numero
negativo: 35-64= -29 !!
-22-12 =-34
TROPPO PICCOLO !!
42+52 = 94 ed anche buttando l’1 in
colonna 7, che vale 64, otteniamo 30, che è
positivo!
overflow o supero
due fatti importanti:
•una somma dà overflow sse i riporti in
colonna n ed n+1 sono diversi
•Se non c’è overflow allora basta buttare
l’eventuale bit in colonna n+1 per ottenere
il risultato corretto
74
test di overflow nel caso di 2 numeri
positivi:
•entrambi hanno 0 in colonna n
•sommandoli, in colonna n+1 il riporto è
sempre 0
•il test dice che la loro somma da supero
sse c’è riporto in colonna n
•la somma è almeno 2n-1 e quindi è
maggiore del massimo intero
rappresentabile con n bits
75
consideriamo ora:
-22-5
111 1
42= 101010+
59= 111011=
1100101
basta buttare via
la regola dice che non c’è
overflow
37-64=-27 OK
esempio:
7 bits, 27=128 quindi
0....63 normali mentre 64...127
rappresentano -64.....-1
-18 ?? -18+128=110
110-128=-18
somma:
63 - 64
63 -> 0111111
-64 -> 1000000
1111111 -> 127 -> -1
non c’è overflow visto che non c’è
riporto nè in colonna 7 nè in 8
altro esempio:
-23 -> 105 -> 1101001
-45 -> 83 -> 1010011
1
11
1101001
1010011
1 0111100
riporto 1 in
colonna 8 e 0
in 7
OVERFLOW
Reali in notazione binaria
bk-1 bk-2 … b2 b1 b0 , b-1 b-2 …
bk-1 x 2 k-1 + bk-2 x 2 k-2 +… + b2 x 22 + b1
x 2 + b0 x 20 + b-1 x 2-1 + b-2 x 2-2 +…
Da decimale a binario:
Per la parte intera, come sappiamo fare
(metodo delle divisioni)
80
REALE--> BINARIO
cosa significa una parte decimale
binaria:
.1101001
2-1+ 2-2 + 2-4 + 2-7
81
.1101001
2-1 2-2...
1.101001
20 2-1.......
moltiplicarlo per 2
significa spostare il
punto di un posto a
destra
se abbiamo un valore decimale in base 10:
0.99 come troviamo la sua rappresentazione
in base 2? Ragioniamo come segue:
supponiamo che .99 = .b1b2b3...bk (binario)
allora 2 .99 = 1.98 = b1.b2b3...bk
quindi b1 è 1
e .98 è rappresentato da .b2b3...bk
per trovare la rappresentazione binaria di
un decimale lo moltiplichiamo per 2 ed
osserviamo se 1 appare nella parte intera:
rappresentazione binaria di
.592= 1.18
.182= 0.36
.362= 0.72
.59
.722= 1.44
.442= 0.88
.100101.....
.882= 1.76
....... dipende da quanti bit
abbiamo
esempio
18.59
18  10010
.59  .100101...
10010.100101....
85
Decimali in forma
normalizzata
43,5 puo’ essere scritto come:
43,5 x 100
0,0435 x 103
4350,00 x 10–3
4,350 x 101 (forma normalizzata)
Lo stesso per i numeri binari decimali:
1001,01 = 1001,01 x 20 = 10,0101 x 22 = 100101,00
x 2–2
Forma normalizzata: la parte intera e’ sempre 1
(es.:1,00101 x 23)
86
Rappresentazione dei
Reali in un computer
1
8
s e+127
23
m
Rappresenta:
N=s
e
2 1.m
implicito
0  e+127  255
quindi
-127  e  128
87
10010.100101...
0 131
0010100101...........
131-127= 4 = numero delle posizioni verso
sinistra di cui abbiamo dovuto spostare il punto
decimale
RAPPRESENTAZIONE UNICA
88
esempio di rappresentazione in
virgola mobile:
12.65 -> 1100.101001...
???
.65*2=1.30 .30*2=.60
.20*2=.40 .40*2=.80
.60*2=1.20
.80*2=1.60 ..
89
1100.101001
mantissa=1.100101001
esponente 130, perchè
130-127=3 e quindi
23* 1.100101001=1100.101001
90
.00101001
deve diventare 1.01001
significa moltiplicare per 23
per rimettere le cose a posto:
esponente 124 visto che
124-127=-3 e
2-3 * 1.01001=.00101001
91
quanti reali si
rappresentano?
•con una parola, cioè 32 bits, possiamo
rappresentare 232 cose diverse al più
232 reali
•questi valori non sono distribuiti
uniformemente come gli interi
•sono maggiormente concentrati tra -1 e 1
•si diradano sempre più allontanandosi
dallo 0
92
Distribuzione disuniforme
Supponiamo 2 bits per la mantissa e 2 per
l’esponente (-1,0,1,2)
0 .5 .6 .7 .8 1 1.2 1.5 1.7 2 2.5 3 3.5 4
5
6
7
93
caratteri
in generale viene usata la codifica ASCII:
ogni carattere è rappresentato da 1 byte:
256 caratteri. Questo basta per:
a....z A...Z
0...9 . , ;: () ..............
caratteri di controllo: enter, tab...
94
wide characters
nel caso sia necessario rappresentare più
caratteri, per esempio gli ideogrammi
cinesi, esiste una codifica che associa 2
bytes ad ogni carattere. In questo modo si
rappresentano 65536 caratteri diversi
95
esercizi
•quali sono le parti principali dell’architettura
di von Neumann?
•citare le caratteristiche salienti della RAM
•quali sono le parti essenziali della CPU
•descrivere il ciclo che la CPU ripete in
continuazione
96
•a cosa servono i registri P e IP della
CPU?
•quali sono gli esempi più comuni di
memoria secondaria e perchè essa si
chiama sequenziale?
•dare alcuni esempi di dispositivi di
input e di output.
esercizi:
•usando la rappresentazione in
complemento a 2, quali valori interi si
possono rappresentare con 5 bits ?
•con 5 bits, realizzare la somma: -5-8,
come si testa se c’è overflow o no?
•con 5 bits, realizzare 10+8, come si testa
se c’è overflow o no?
98
esercizi
•dare la rappresentazione in virgola
mobile normalizzata dei valori 0.5, 1.5 e
10.543 avendo 8 bits per l’esponente e 8
per la mantissa.
99