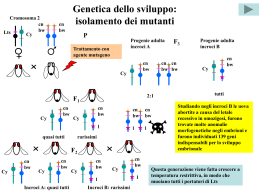
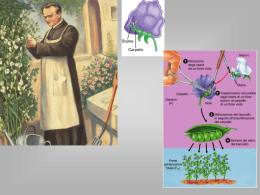
L’evoluzione biologica
Secondo Lamarck
Le condizioni ambientali (albero
alto) stimolano un cambiamento
adattativo dei caratteri
(allungamento del collo); il
cambiamento del carattere viene
ereditato dalla progenie (tutta con
il collo lungo); secondo questa
ipotesi i caratteri acquisiti sono
ereditabili.
Secondo Darwin
Il carattere (lunghezza del collo) è
variabile; le condizioni ambientali
(albero alto) causano la
competizione dovuta alla lotta per
la sopravvivenza; solo gli animali
con il carattere favorevole (collo
lungo) riescono a sopravvivere e a
passare il carattere favorevole alla
propria progenie; questo processo
viene detto selezione naturale
L’ipotesi di Lamark
(eredità dei
caratteri acquisiti)
si è rivelata falsa
La teoria di Darwin (variabilità
preesistente dei caratteri su cui
opera la selezione derivata dalla
competizione per le risorse
ambientali, eredità dei caratteri
selezionati) si è rivelata corretta
La distribuzione del carattere “peso del seme” nella F2
dell’incrocio fra due linee pure di fagiolo in ambiente omogeneo
Coefficienti binomiali
ppss
PPSS
Generazione P
n
=
n!/k!(n-k)!
k
ps
PS
PpSs
Gameti
Generazione F1
Gameti
Ps
pS
PS
PPSS
PPSs
PpSS
PpSs
Ps
PPSs
PPss
PpSs
Ppss
pS
PpSS
PpSs
ppSS
ppSs
ps
PpSs
Ppss
ppSs
Gameti
Distribuzione binomiale dei
fenotipi della F2
ps
PS
Genotipi della F2
ppss
Fenotipi della F2
È possibile selezionare il carattere “peso del seme”, la cui
variabilità è determinata geneticamente
Fenotipi della F2
Selezione per il seme grande
Selezione per il seme piccolo
Gameti
pS
Gameti
ps
PS
ppSs
ppSS ppSs pS
ppSs
Ps
PPSs
Gameti
Gameti
ppss ps
PS
PPSS
PPSs
Ps
PPSs
PPss
Genotipi delle F3
…verso il peso
del seme piccolo
Fenotipi delle F3
La selezione è stata efficace: nelle 2 progenie della
F3 si è ottenuto effettivamente uno spostamento del
peso medio dal seme normale nella F2…
…verso il peso del
seme grande
La variabilità del peso dei semi in una linea pura di
fagioli mantenuta in un ambiente eterogeneo è dovuta
solo a cause ambientali: la selezione è inefficace
Distribuzione per il peso dei semi in
una linea pura di fagioli con
genotipo PPSS
Si selezionano e si
incrociano le piante
con i semi “piccoli”
Gameti PS x
gameti PS
La variabilità del carattere “peso del
seme” è dovuta esclusivamente alla
variabilità ambientale
Si selezionano e si
incrociano le piante
con i semi “grandi”
Gameti PS x
gameti PS
fecondazione
fecondazione
Progenie PPSS
La progenie è mantenuta
nello stesso ambiente della
generazione precedente,
Progenie PPSS
La distribuzione per il peso de semi, in particolare il
peso medio, non varia fra le generazioni
La
selezione è
inefficace
Le fonti della variabilità genetica
Perché sia possibile l’evoluzione, la selezione deve operare su una preesistente
variabilità genetica; ma per effetto della selezione la variabilità genetica viene
ridotta nelle generazioni successive, poiché si trasmettono alla progenie solo gli alleli
e i genotipi più adatti all’ambiente.
Ma per adattarsi a un ambiente mutevole, le specie debbono mantenere un livello adeguato
di variabilità genetica per rispondere tempestivamente alla mutabile pressione selettiva.
Fonti primarie
Mutazioni geniche
Poliploidia, duplicazioni
Nuovi alleli
Geni duplicati
Nuovi geni
Amplificazione
(esponenziale)
Riproduzione sessuale
Ricombinazione
Nuove combinazioni di alleli
Localmente
Migrazioni
Nuovi alleli (localmente)
L’origine di nuovi geni
L
B’: allele
funzionale di B
M N
Duplicazione
L
M M N
Mutazioni
geniche
M
L
M M’ N
L
M m1 N
L
M m2 N
Diverse
mutazioni
geniche
L
m1, m2: alleli non
funzionali di M
Regione duplicata
m, m’: prodotti
del gene M
O: nuovo gene
m
Sostanza 1
o
Sostanza 3
Sostanza 2
m’
Sostanza 1
MO N
Sostanza 1
Sostanza 4
o: prodotto
del gene O
La genetica delle popolazioni
La genetica di popolazione si occupa della frequenza degli alleli nelle
popolazioni e del loro andamento nel tempo, quindi studia la variabilità
genetica e i fattori che ne influenzano nel tempo i cambiamenti, mirando alla
comprensione dei meccanismi genetici alla base dell’evoluzione.
La genetica formale studia i risultati di
singoli incroci fra 2 individui, che, per i geni
studiati, possono avere al massimo 2 alleli
diversi (se sono eterozigoti); nell’incrocio
tra 2 eterozigoti, ciascuno produce metà
(0,5) gameti con il 1° allele, metà con il 2°;
nella progenie ci si aspetta che un quarto
(0,25) sia omozigote per il 1° allele, un
quarto sia omozigote per il secondo e metà
eterozigote.
A1 0,5
La genetica di popolazione studia i risultati
di tutti i possibili incroci fra tutti gli
individui di sesso opposto della
popolazione, immaginando di mettere
insieme tutti i gameti dello stesso sesso e di
accoppiare casualmente a 2 a 2 i gameti di
sesso opposto; per i geni studiati il numero
degli alleli diversi può essere qualsiasi,
come può esserlo la loro frequenza.
A1
0,2
A2
0,3
A3
0,5
A1 0,2
A1A1
0,04
A1A2
0,06
A1A3
0,1
A2 0,3
A1A2
0,06
A2A2
0,09
A2A3
0,15
A3 0,5
A1A3
0,1
A2A3
0,15
A3A3
0,25
A2 0,5
A1 0,5 A1A1 0,25
A1A2 0,25
A2 0,5 A1A2 0,25
A2A2 0,25
Una popolazione si dice polmorfa per un
gene, se per esso presenta più di un allele; si
dice monomorfa se presenta un solo allele
Le leggi di Hardy-Weinberg
1° legge di Hardy-Weinberg: le frequenze degli alleli in una popolazione non
cambiano passando da una generazione all’altra se:
1) Non c’è selezione
2) Non c’è mutazione
3) Non c’è migrazione
4) La popolazione è infinitamente grande
Se pn è la frequenza relativa dell’allele A1 alla generazione n, quando le 4 condizioni sono
rispettate, la popolazione è all’equilibrio (e non c’è evoluzione!) e:
pn+1 = pn; pn+1-pn= p=0
A1 p
A2 q
A3 r
A1
p
A2
q
A3
r
A1A1
p2
A1A2
pq
A1A3
pr
A1A2
pq
A2A2
q2
A2A3
qr
A1A3
pr
A2A3
qr
A3A3
r2
2° legge di Hardy-Weinberg: le frequenze dei
genotipi diploidi in una popolazione sono
uguali al prodotto delle frequenze degli alleli
(se queste ultime sono i coefficienti di un
polinomio, le prime sono i coefficienti del
quadrato del polinomio ) se:
1) C’è panmissia, cioè se ogni incontro tra i
gameti di sesso opposto ha la stessa probabilità
Se p e q sono le frequenze relative degli
alleli A1 e A2 in una data generazione, le
frequenze relative dei genotipi A1A1,
A1A2 e A2A2 della stessa generazione
sono, rispettivamente: p2, 2pq e q2
Mutazione, migrazione e selezione
MUTAZIONE
MIGRAZIONE
Se A2 muta in A1 a un tasso
costante m per generazione, allora:
p=mq
Se da una popolazione donatrice, in cui A1 ha
una frequenza P, immigra una frazione m della
popolazione ricevente per generazione, allora:
p=m(P- p)
SELEZIONE
L’idoneità riproduttiva
(“fitness” – W) di un
genotipo (per il genotipo
A1A2, WA1A2) è la sua
probabilità di
sopravvivere e produrre
progenie feconda
Il progressivo
cambiamento delle
frequenze alleliche può
portare ai valori p=0 o
p=1
La fitness media di una popolazione
è W’=p2WA1A1+2pqWA1A2+ q2WA2A2
La fitness media dell’allele A1 è
W’A1=pWA1A1+qWA1A2
La selezione determina
un cambiamento delle
frequenze alleliche a
causa della differente
fitness degli alleli:
p=pq(W’A1-W’A2)/W’
Quando p=1, l’allele
A1 è fissato nella
popolazione; quando
p=0, l’allele A1 è
eliminato
Quando un allele è fissato e gli altri
sono eliminati, la popolazione da
polimorfa diviene monomorfa e in
essa non sono più possibili
variazioni delle frequenze alleliche
Variazioni della frequenze alleliche
dovute a diversi tipi di selezione
A1A1
A1A2
A2A2
Dp
Direzionale
positiva recessiva
1
1-s
1-s
sp2q/W’
Direzionale
positiva dominante
1
1
1-s
spq2/W’
Stabilizzatrice
1-s
1
1-s
spq(q-p)/W’
Diversificatrice
1
1-s
1
spq(p-q)/W’
s=1-w (per ogni genotipo)=
coefficiente di selezione
Bilanciamento fra mutazione e selezione
Se un allele dannoso A1 con coefficiente di selezione s viene introdotto in
una popolazione a un tasso costante di mutazione per generazione m, sono
raggiunte le seguenti frequenze all’equilibrio p^.
Per un allele recessivo
Per un allele dominante
p^=(m/s)1/2
p^=m/s
Effetti dei diversi tipi di selezione sulla
variabilità genetica delle popolazioni
L’allele
selezionato,
per la
selezione
direzionale, è
l’allele
azzurro scuro
Equilibrio
indifferene
Equilibrio
stabile
Equilibrio
instabile
Selezione
direzionale
positiva
Selezione
direzionale
negativa
Selezione
stabilizzatrice
Selezione
diversificatrice
Diversi tipi di selezione: conseguenze evolutive
La selezione direzionale
Avvantaggia uno dei 2 genotipi omozigoti (A1A1) e svantaggia l’altro genotipo omozigote
(A2A2) e il genotipo eterozigote (A1A2) (effetto vantaggioso recessivo per A1, svantaggioso
dominante per A2: WA1A1>WA1A2=WA2A2)
Avvantaggia uno dei 2 genotipi omozigoti (A1A1) e il genotipo eterozigote (A1A2) e
svantaggia l’altro genotipo omozigote (A2A2) (effetto vantaggioso dominante per A1,
svantaggioso recessivo per A2: WA1A1=WA1A2>WA2A2)
L’effetto della selezione direzionale è comunque la fissazione dell’allele avvantaggiato e
l’eliminazione dell’allele svantaggiato
La selezione stabilizzatrice
Avvantaggia il genotipo eterozigote (A1A2) e svantaggia i genotipi omozigoti (A1A1, A2A2)
WA1A2>WA1A1; WA1A2>WA2A2)
L’effetto della selezione stabilizzatrice è la persistenza di entrambi gli alleli con frequenze
all’equilibrio diverse da 0 e 1; il valore di queste frequenze dipende dalle fitness dei genotipi
La selezione diversificatrice
Svantaggia il genotipo eterozigote (A1A2) e avvantaggia i genotipi omozigoti (A1A1, A2A2)
WA1A2<WA1A1; WA1A2<WA2A2)
L’effetto della selezione diversificatrice è la fissazione di uno dei due alleli e l’eliminazione
dell’altro; quale allele venga fissato e quale eliminato dipende dalle frequenze alleliche
L’assenza di selezione
La deriva genetica
Quando una popolazione è molto grande (oltre le migliaia di individui) può essere
assimilata a una popolazione infinitamente grande: in assenza di altri fattori, le
frequenze degli alleli rimangono costanti con il passare delle generazioni
Più piccola è una popolazione, più è probabile che, per caso, le frequenze degli alleli
cambino ad ogni generazione: questo fenomeno è chiamato deriva genetica
Le probabilità delle frequenze alleliche alla generazione successiva hanno una
distribuzione binomiale (coefficienti delle potenze di un binomio); la variazione della
frequenza allelica tra 2 generazioni può essere sia un aumento che una diminuzione; le
variazioni piccole, in valore assoluto, sono più probabili di quelle grandi
La deriva genetica porta alla
fissazione di un allele e
all’eliminazione degli altri; più
piccola è la popolazione, più rapido
è il processo
Un allele neutrale appena sorto per
mutazione in una popolazione di N
individui ha una frequenza iniziale 1/2N,
una probabilità 1/2N di essere fissato e
(2N-1)/2N di essere eliminato
La deriva genetica
Quando una popolazione è molto grande (oltre le migliaia di individui) può essere
assimilata a una popolazione infinitamente grande: in assenza di altri fattori, le
frequenze degli alleli rimangono costanti con il passare delle generazioni
Più piccola è una popolazione, più è probabile che, per caso, le frequenze degli alleli
cambino ad ogni generazione: questo fenomeno è chiamato deriva genetica
Le probabilità delle frequenze alleliche alla generazione successiva hanno una
distribuzione binomiale (coefficienti delle potenze di un binomio); la variazione della
frequenza allelica tra 2 generazioni può essere sia un aumento che una diminuzione; le
variazioni piccole, in valore assoluto, sono più probabili di quelle grandi
La deriva genetica porta alla
fissazione di un allele e
all’eliminazione degli altri; più
piccola è la popolazione, più rapido
è il processo
Un allele neutrale appena sorto per
mutazione in una popolazione di N
individui ha una frequenza iniziale 1/2N,
una probabilità 1/2N di essere fissato e
(2N-1)/2N di essere eliminato
Esempi di cambiamenti casuali delle frequenze alleliche per deriva genetica a
partire da p=0,5 fino alla fissazione o all’eliminazione dell’allele azzurro scuro
probabilità di variazione delle frequenze alleliche da una
generazione all’altra per deriva genetica
La probabilità che un allele con frequenza pi nella generazione i in una popolazione di
n/2 individui diploidi assuma alla generazione i+1 la frequenza pi+1 = k/n è la seguente:
n
k
pik(1-p)n-k
in cui
n
=
n!/k!(n-k)!
k
In una popolazione di 3 individui bisessuati- uno A1A1, uno A1A2 e uno A2A2 –
p=q=0,5=1/2 se si estraggono casualmente i gameti che portano gli alleli A1 e A2, si
avranno nella generazione successiva, sempre di 3 individui, le seguenti frequenze
alleliche p di A1con le seguenti probabilità:
p=1/6
p=1/3
p=1/2
p=2/3
p=5/6
p=1
p=0
frequenza
probabilità
1/64
6/64
15/64
20/64
15/64
6/64
1/64
Mentre il valore di Dp è, per ogni valore di pi, univocamente determinato per segno e per
valore, se agiscono come fattori evolutivi la selezione, la mutazione o la migrazione, c’è una
distribuzione stocastica di valori, sia in aumento che in diminuzione, se il fattore evolutivo è
la deriva genetica.
L’incrocio preferenziale
L’incrocio preferenziale è una delle modalità di incrocio diverse dalla panmissia
Se, in una popolazione con 2 alleli (A1 e A2) per il gene A, si incrociano tra loro gli
individui con lo stesso genotipo (omozigoti A1A1 fra loro, omozigoti A2A2 fra
loro, eterozigoti A1A2 fra loro, ad ogni generazione si riduce la frequenza degli
eterozigoti.
A1A1
A2A2
Generazione n
Generazione n+1
A1A2
Generazione n+2
Le frequenze degli omzigoti (f(A1A1) ed f(A2A2) sono più alte di quelle attese in base
alla 2° legge di Hardy Weinberg, quella degli eterozigoti (f(A1A2)) è più bassa; questo
allontanamento dall’equilibrio procede sempre di più con il passare delle generazioni.
f(A1A1)>p2; f(A2A2)>q2; f(A1A2)<2pq
Per calcolare p e q, anche in assenza di panmissia, ci si basa sulle frequenze
genotipiche reali: p=f(A1A1)+0,5f(A1A2); q=f(A2A2)+0,5f(A1A2)
Sintesi sugli effetti dei fattori evolutivi
Mutazione
Migrazione
Deriva genetica
Selezione diversificatrice
Selezione stabilizzatrice
Selezione direzionale svantaggiosa
Selezione direzionale vantaggiosa
0
1
p
Fattore evolutivo
Selezione direzionale vantaggiosa
Selezione direzionale svantaggiosa
Selezione stabilizzatrice
Selezione diversificatrice
Deriva genetica
Migrazione
Mutazione
Valore di equilibrio stabile per p verso cui la
selezione stabilizzatrice fa convergere p
Valore di equilibrio instabile per p da cui la
selezione diversificatrice fa divergere p
Effetto sulla variabilità
entro le popolazioni
Effetto sulla variabilità
tra le popolazioni
+
+
+
+
+
-
Picchi adattativi
xxYYzz
XXYYZZ
s
e
l
e
z
i
o
n
e
XXyyzz
xxYYzz
xxyyzz
XXyyzz
Deme
xxyyzz
XXyyZZ
xxYYzz
XXYYZZ
XXyyzz
xxyyzz
XXyyZZ
s
e
l
e
z
i
o
n
e
XXYYZZ
XXYYZZ
XXYYZZ
XXyyZZ
XXyyzz
XXYYZZ
Metapopolazione