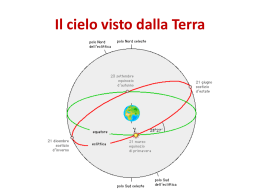
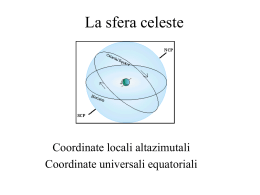
Coordinate Terrestri
ψ = Longitudine (psi)
φ = Latitudine (fi)
asse rotazione
terrestre
O = Osservatore
O
G 
φ
C

ψ
Equatore Terrestre
(ET)
G = Greenwich
C = Centro Terra
Coordinate Orizzontali Locali
(altazimutali)
z
Z
A = azimuth
h = altezza
Sfera Celeste

P
O

y Est
Asse z = verticale locale
Z = zenit
h
A
O = Osservatore
x
Nord
Orizzonte Celeste
(HC)
Coordinate Equatoriali Locali o
orarie
z
H = angolo orario
δ = declinazione
PN

Sfera Celeste
Z

O = Osservatore
P
O

y Ovest
δ
H
x
Sud
Equatore Celeste
(EC)
Asse z = linea dei poli
PN = polo Nord
N.B. – δ indipendente da posizione
e istante di osservazione
Coordinate Equatoriali Assolute o
celesti
 = ascensione
δ = declinazione
PN
Sfera Celeste

P


x
O


δ
O = Osservatore
y
Sud
Equatore Celeste
(EC)
 = punto vernale
punto fisso  intersezione dell’eclittica con Ec (quella in corrispondenza del
passaggio del Sole dall’emisfero Sud a quello Nord: equinozio di primavera)
Confronto tra Sistemi di Coordinate
HC
Z

EC
O
C

C = Centro Terra
O = Osservatore
Z = zenit di O
φ
ET
ET = equatore terrestre
EC = equatore celeste
HC = orizzonte celeste
asse rotazione
terrestre
Tempo Siderale …
angolo orario del punto vernale
Z

per un generico
oggetto, risulta:

O
N
tsid. = H + α

H
S
α
HC

EC
… Tempo Siderale
Terra e Sole all’equinozio
di primavera
Posizioni A e B  sfera
celeste appare identica
all’osservatore: è trascorso
un giorno siderale
Giorno siderale dura meno
di quello solare medio:

A
B
Δt =
24
h = 3’ 56”.56
365.2564
N.B. – dopo 1 anno, tempo solare e siderale sono di nuovo in fase

gg. (anno siderale) = gg. (anno solare) + 1