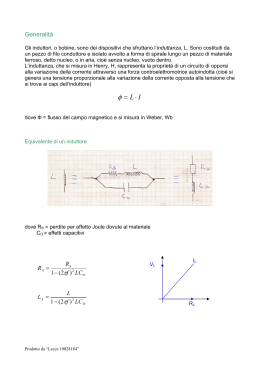
Ing. Ambiente&Territorio
Ing. Civile
Esame di Elettrotecnica
11 giugno 2007
Nome: _______________ Cognome: ________________ Mtr: _______
V
V  220 V
z  3  j 4 W
z
Nel circuito in figura, determinare il valore della capacità che rifasa completamente il carico assegnato.
Determinare, inoltre, di quanto si riduce il modulo della corrente di linea, nel passare dalla configurazione
iniziale a quella con il capacitore di rifasamento
C
vi
L
R
vo
L = 2 mH
C = 5 mF
R = 10 W
Il circuito in figura ha i componenti scarichi nell’istante t = 0.
Il generatore vi è un gradino unitario: vi(t) = d-1(t)
Determinare l’andamento di vo(t) per t > 0
a
100 W
Vb
Va
Vc
b
100 W
c
100  j50 W
Nel circuito in figura, il generatore è simmetrico con
valore efficace: V = 380 V
Come si può osservare, il carico è squilibrato, e
questo comporta uno spostamento del centro stella.
Determinare il valore della tensione a cui è
sottoposto il carico monofase ohmico-induttivo,
collegato alla fase c.
4,92 cm
0,87 cm
N = 407
0,79 cm
4,24 cm
i
Determinare l’induttanza dell’avvolgimento in figura,
nella quale sono descritte le caratteristiche
geometriche del sistema, tenendo presente che:
•le sezioni dei gioghi e delle colonne sono quadrate,
•la permeabilità relativa del mezzo è pari a 900
•si considerano nulli i flussi dispersi
4,92 cm
0,87 cm
N = 407
4,24 cm
i
Determinare l’induttanza dell’avvolgimento in
figura, nella quale sono descritte le caratteristiche
geometriche del sistema, tenendo presente che:
•le sezioni dei gioghi e delle colonne sono
quadrate,
•la permeabilità relativa del mezzo è pari a 900
•si considerano nulli i flussi dispersi
0,79 cm
Svolgimento
Rc
NI
Rc 
Rg
Rg
F Rc
Rg
Rg
Anzitutto costruiamo il circuito elettrico equivalente, secondo
l’analogia magneto-elettrica (fig. a lato).
La tensione del generatore è pari alla f.m.m.
Rc dell’avvolgimento, pari a NxI As, dove N = 407 spire.
Le riluttanze delle 3 colonne sono tra loro uguali, così come
sono uguali tra loro le riluttanze dei 4 gioghi. Procediamo al
loro calcolo:
0,0424
 4,95  105 H -1
4π  10  900  0,00087 2
-7
Rg 
0,0246
 3,49  105 H -1
4π  10  900  0,000792
-7
Si può quindi procedere al calcolo della resistenza equivalente vista dal generatore:
Req  Rc  Rg  Rc // 2 Rg  Rc   Rg 
R  2 Rg  Rc 
4,95  105  2  3,49  105  4,95  105
 Rc  2 Rg  c
 4,95  105  3,49  105 
 11,94  105 H -1
5
5
5
Rc  2 Rg  Rc 
4,95  10  2  3,49  10  4,95  10


NI
F
Rc


Il circuito elettrico equivalente si riduce al circuito raffigurato a lato,
per il quale è immediato calcolare l’intensità di corrente, che
corrisponde al flusso circolante nella colonna di sinistra:
NI
407
F

 I  3,41  10-4  I Wb
5
Req 11,94  10
Moltiplicando per il numero N di spire del’avvolgimento otteniamo il flusso concatenato:
F c  N  F  407  3,41  10-4  I  0,139  I Wb
L’induttanza è data dal rapporto tra tale flusso concatenato e la corrente I:
L
Fc
 0,139 H
I