Cinematica
Determinazione del moto – 1 dimensione
v
t
d
a  v  dv  adt   dv   adt
dt
v
t
0
0
t
v  v 0   adt
t0
a0
v  v0  cost
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
a  cost
v  v 0  at
Capitolo 2 Cinematica
1
1
Cinematica
Determinazione del moto – 1 dimensione
x
t
d
v  x  dx  vdt   dx   vdt
dt
x
t
0
v0
x  x0  cost
1 2
1+2  x  x0  v0 t  at
2
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
0
v  cost
x  x0  v 0 t
2
Moto uniformemente accelerato
Capitolo 2 Cinematica
2
Moto nel piano
Cinematica
y
x  r cos 
y  r sin 
P
r
r t 

x
O
x2  y2
y
tan  
x
vettore OP

r t   OP  x( t )uˆ x  y( t )uˆ y
û y
uˆ  vettore unitario  versore
û x
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
3
Determinazione del moto – 1 dimensione
Cinematica

r t 

r

r  t  t 
 d 
v r
dt


r ( t  t )  r ( t )

v  lim
t
t  0
velocità
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
4
Determinazione del moto – 1 dimensione
Cinematica
La velocità è sempre tangente alla traiettoria

r
S

dr

ds


dr  ds  uˆ t
 d
v  s  uˆ t
dt
uˆ t versore tangente alla traiettori a
in coordinate cartesiane
d
d
 d  d
v  r  ( xuˆ x  yuˆ y )  ( x )uˆ x  ( y )uˆ y  v x uˆ x  v y uˆ y
dt
dt
dt
dt
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
5
Cinematica
Determinazione del moto – 2 dimensioni
 
 

dv  adt  v  v 0  at
Il vettore velocità è sempre nel
piano individuato dai vettori


costanti v 0 e a
{
v x  v0 x  a x t
v y  v0 y  a y t
1
 
  
dr  vdt  r  r0  v0 t  at 2
2
Proiezione del moto in due dimensioni
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
{
1
x  x0  v 0 x t  a x t 2
2
1
y  y0  v 0 y t  a y t 2
2
Capitolo 2 Cinematica
6
Moto parabolico
Cinematica
 

a  g   guˆ u

g
y
v0

x
Moto lungo x
x  v0 cos  t
condizioni iniziali
 x0  0

r0  0  
 y0  0
v 0 x  v cos 

v0

v 0 y  v sin 
v x  cost  v0 cos 
Moto lungo y
1
y  (v 0 sin  )t  gt 2
2
v y  v 0 sin   gt
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
y( x )  x tan  
g
2v02 cos 2 
x2
Parabola!
Capitolo 2 Cinematica
7
Moto parabolico
Cinematica

v0
o
Gittata : y  0
xM

v0
Altezza massima
v 02 sin 2 
y( x M ) 
2g
Tempo di volo
2xM
2 x M 2v 0 sin 
tG 


v 0 cos 
vx
g
tG  tempo di salita
2
tG  tempo di discesa
2v 02 cos  sin  2v 02 sin( 2 )
xG 

g
g
v 02 cos  sin 
x M  xG 
g
2
Angolo per cui si
ottiene la gittata massima
d
xG  0    45
d
v 02
se   45  xG 
g

2
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
8
Colpisci un bersaglio
Cinematica
y
v0
y0 
Lanciamo un proiettile con velocità v 0 orizzontale.
Vogliamo colpire il punto x0
x0
x0  v 0 t  v 0
x
2 y0
1
y  y0  v 0 y t  gt 2  t 
2
g

0
x0
2v02
tan  

y0
gy0
2 y0
g
Bisogna lanciare il proiettile
quando l’angolo è
 2v 2 
0
  arctan 

 gy0 
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
9
Colpisci un bersaglio
Cinematica
P( x 0 , y0 )

v0

Proiettile
Bersaglio
1 2
1 2
y1  v oy t  gt
y 2  y0  gt
2
2
y1  y2
y0
1 2
1 2
v0 y t  gt  y0  gt  t 
2
2
v0 y
nel tempo :
y
v
t  0 ; x1  v0 x t  0 x y0 ; x 2  x0
v0 y
v0 y
v0 x
v 0 x x0
se imponiamo x1  x2 
y0  x 0 

v0 y
v 0 y y0
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
10
Coordinate polari
Cinematica
ûT

r
 
In questo caso r  r uˆ N
 d  d 
 d
v  r  r uˆ N  r uˆ N
dt
dt
dt
û N

o
Derivata di un versore!
 d 
 d
v  r uˆ N  r uˆT
dt
dt
Componente normale
Componente tangenziale
(Velocità radiale)
(Velocità trasversale)

vT

r
Modulo della velocità

vN
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
2
d
d 
d 
v  s   r   r2  
dt
 dt 
 dt 
Capitolo 2 Cinematica
11
2
Accelerazione nel moto piano
Cinematica
ûT
 d  d2 
a v 2r
dt
dt
ûT
û N
d
 
scriviamo la velocità come v  v uˆT
uˆ t varia nel tempo
d
d
 d

ˆ

ˆ
a
vuT  v uT  v uˆT
dt
dt
dt
û N
Derivata di un versore!
d
 d
a  v uˆT  v  uˆ N
dt
dt
aT
aN
v2
 d
a  v uˆT 
uˆ N
dt
R
aT
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
aN

2
a  aT2  a N
Capitolo 2 Cinematica
12
Derivata di un versore
Cinematica
S
uˆ  uˆ ( t  t )  uˆ ( t )
   (oppure t  0)
û
duˆ
ût   ût 
S  uˆ 
ma dS  duˆ
 uˆ  duˆ
duˆ  uˆ

da cui
dS  uˆ d
duˆ  uˆ d
duˆ  d
1
d
d
uˆ  
dt
dt
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
13
Accelerazione centripeta o normale
Cinematica
aT
d
 d
a  v uˆT  v  uˆ N
dt
dt
aN
ûT
Per una circonferenza
di raggio R…
dS
û N
d
ûT
û N
d
d d
1
  s v
dt
ds dt
R
da cui
aN
v2
 uˆ N
R
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
14
Moto circolare uniforme
Cinematica
v
v2
 d
a  v uˆT 
uˆ N
dt
R


v  v x uˆ x  v y uˆ y  v  ( v sin )uˆ x  (v cos )uˆ y
aN
v
aN

v


v
yP
P
vx
yP
R
xP
cos  
R
sin  
vy
v yP
v xP

v  (
)uˆ x  (
)uˆ y
R
R

xP
v d
v d
 d 
ˆ
a v
yP ux 
x P uˆ y
dt
R dt
R dt
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
15
Moto circolare uniforme
Cinematica

 v2

  v 2


a    cos   uˆ x    sin   uˆ y
 R

 R

ax
a

ay
2
v

a  a 2x  a 2y 
R
tan  
ay
ax
 tan 
Il vettore a è diretto verso il centro
e vale v²/R in modulo
ûT
ûT
û N
Attenzione:
aN  0
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
û N
aN  0
Capitolo 2 Cinematica
16
Moto circolare – coordinate polari
Cinematica
S t    t r
P
r
con r  costante
 t 
S


d
1d
v

S
dt
r dt
r
a
d d2
1d
   2 
v T
dt dt
r dt
r
v  r 
aT  r 
Ricordiamo che in coordinate polari
 d 
 d
v  r uˆ r  r uˆ
dt
dt
v  r
0
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
Capitolo 2 Cinematica
17
Moto circolare – coordinate polari
Cinematica
x 
v 
a 
aT  r
aN
Moto circolare uniformemente
accelerato
1 2
 t   0   0 t  t
2
 t   0 t
 t   cost
Politecnico di Bari, Laurea in Ingegneria Elettrica
Corso di Fisica Sperimentale I
Prof. G. Iaselli
aT
v2

  2r
R
aN
Moto circolare uniforme
  t   0   0 t
 t   0
 t   0
Capitolo 2 Cinematica
18
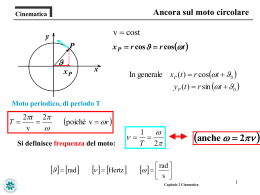
Ancora sul moto circolare
Cinematica
v  cost
y
x P  r cos   r cos t 
P

xP
x
In generale xP (t )  r cost  0 
yP (t )  r sin t  0 
Moto periodico, di periodo T
2r 2
T

v

poichè v  r 
Si definisce frequenza del moto:
   rad 

   Hertz 
1 

T 2
anche   2 
    rad 
 s 
Capitolo 2 Cinematica
19
Moti relativi – Traslazione

OO  vt t
y
'
y
'
P

r

r'
O'
O
x
moto relativo uniforme
'  
r  r  vt t
'
x

vt
'
dr  '  
 v  v  vt
dt
'  
v  v  vt
Trasformazione della velocità di Galilei
Se

v t  cost

 ' d v
' 
a 
 a a
dt
 x '  x  vt t
 '
y  y
t '  t

v x '  v x  v t
 '
v y  v y
'
t  t
Invarianza dell’accelerazione nel caso di moti relativi uniformi
20
Moti relativi – Traslazione
Sistema fisso

v
y
y

tan  

v0
O


vt
O'
vy
vx
x'
vy
vy
tan   

vx v x  v t
In particolare se
y
'
v
'
x
O
'
Sistema in moto
y'
vt  vx
x
v 0 cos 
'
v

vt
x21'
Un altro esempio – Traslazione
Cinematica
y

v
y
O
Nel sistema di riferimento

in moto con velocità v

vt
'
O
y'
'
'
v
x
x'
Dalle trasformazioni di Galileo:
O'
x'
'  
v  v  vt
'

v
 x  v t
 '

v y  v y   v

v'  v 2  v 2t
t
'
v

vt

v
vt
tan  
v
22
Moti relativi – Traslazione con v ≠ cost
Cinematica
v t  cost

 '  dv t
a a
dt
'  
a  a  at

a t accelerazione di trascinamento
Esempio:
Nel sistema fisso il punto P è in quiete
y

O' a t
P
'  
a  a  at

at
0
O
x
Nel sistema in moto accelerato P si

muove con un’accelerazione  a t
23
Un altro esempio
Cinematica
Ascensore in caduta libera
x
O
O'
x'
Nel sistema fisso un oggetto nell’ascensore
“cade” con l’accelerazione g
Nel sistema in moto con accelerazione g:
g
at  g
y'
y
'  
a  a  at
'
a  gg0
Nel sistema in movimento non si sente alcuna accelerazione!
(assenza di gravità)
Capitolo 2 Cinematica
24
Sempre da un sistema in caduta libera…
Cinematica
y
v0
Nel sistema in caduta libera

g
ay  g
ax  0

at
x
O
'  
a  a  at
a  0  v  cost
'
x
'
x
a  0  v  cost
'
y
y'
'
y
O'
a 'x  a x  0

g
x'
a 'y  a y  a t   g  (  g )  0
Traiettoria rettilinea
'

v
 x  v 0 cosα  ' 
 v  v0
 '

v y  v 0sin α
25
Moto relativo di rotazione
Cinematica
  cost
Supponiamo il punto P in moto con   cost


nel sistema fisso
  
v  r

P
In generale
'   
v  v   r
Nel sistema in rotazione:

v'  0
oppure
 
 
v  v'    r
Nel sistema rotante non c’è accelerazione!
Nel sistema fisso il moto è accelerato!
Capitolo 2 Cinematica
26
e l’accelerazione?
Cinematica
 '  
v  v   r
d  d '  d  d  
v  v    r   dr
dt
dt
dt
dt
0



 
   
 
a  a'    r    v '    r

 
  
 
a  a '  2   r      r 
accelerazione centripeta
accelerazione di Coriolis
Capitolo 2 Cinematica
27
Un caso semplice
Cinematica
Supponiamo il punto P si muova di moto uniforme nel sistema fisso
Nel sistema rotante
'
 ' 
 
a  2   v      r 

O
P
Sistema fisso

v'

 
     r 
aT
P
P
'
a
 
 2  v'
aN
Sistema rotante
a N   2r
aT  2 v 2   2 r 2
Capitolo 2 Cinematica
28