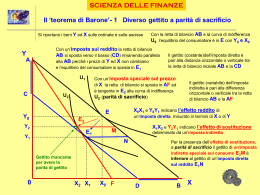
SCIENZA DELLE FINANZE
Il massimo gettito di un’imposta indiretta (Dupuit 1844) - 2
p e costo marginale cma, sulle ascisse la quantità q;
d è la domanda, che con cma ha un equilibrio in E, con p0 e q0
Sulle ordinate sono prezzo
Con l’imposta unitaria T1 in N (punto medio di AE) il gettito dell’imposta indiretta
A
p
p1 Nvp0 è massimo: è l’area massima di un poligono inscrivibile in AEp0
cma
b
p3
T3
h
p1
Un’imposta unitaria T3 porta il prezzo a p3 e dà un gettito di p3bsp0, che è
un’area inferiore a p1Nvp0: di fronte all’aumento di gettito hbp3p1 si ha una
perdita di gettito superiore (hNvs), che diventa un maggior eccesso di pressione
per aumentare il gettito bisogna ridurre l’imposta unitaria
N
T1
g
p2
Passando da b a N: p1Ngp2 > p3bhp1
e diminuisce l’ imposta unitaria ma
cresce il gettito complessivo
f
T2
E
p0
s
v
m
Un’imposta unitaria T2 porta il prezzo a p2 e dà un
gettito di p2fmp0, che è un’area inferiore a p1Nvp0
per aumentare il gettito bisogna aumentare
l’imposta unitaria
cma
d
0
q3
q1
q2
q0
Passando da f a N si ha p1Ngp2 > fmvg
e aumenta sia l’imposta unitaria che il gettito
complessivo
q