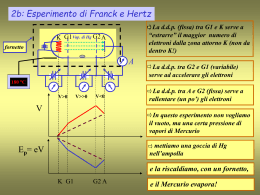
Appunti di Complementi di Fisica Atomica
di
Elio Colavita, Tommaso Caruso e Vincenzo Formoso
Modello di Bohr dell’atomo
n 40
rn 
Z me2
2
• orbite circolari:
2
• energia dipende soltanto da n:
4
2
2
1 e m Z
Z
En  
 R 2
2
2
2 (4 0 ) n
n
4
1 e m
R
 13.6eV costante di Rydberg
2
2 (4 0 )
Modello di Sommerfeld dell’atomo
•orbite ellittiche: an=a0n2/Z ; bn= a0nk/Z.
•energia dipende soltanto da n:
1 e4 m Z 2
Z2
En  
 R 2
2
2
2 (4 0 ) n
n
R costante di Rydberg
Nota bene

•Possono esistere più orbite in corrispondenza
dello stesso valore di energia:degenerazione.
•La ellitticità dell’orbita dipenda dal numero
quantico k.
Esperienza di Franck ed Hertz
•Dimostra la quantizzazione dell’energia
dell’atomo;
•Dimostra che l’atomo è caratterizzato
dalla sua struttura energetica;
•Dimostra che l’energia può essere
assorbita dall’atomo secondo quantità
definite dalla sua struttura energetica.
3
Esperienza di Stern e Gerlach dimostra
l’esistenza del numero quantico di spin.
Ciascuno stato è quindi caratterizzato da
quattro numeri quantici: n, l, ml, ms .
Uno stato energetico può essere degenere
rispetto ad l, ml, ms .
Una perturbazione esterna o interna può
togliere l’eventuale degenerazione.
Moto del vettore momento
angolare J
Il vettore J precede intorno alla
direzione del campo magnetico
interno Bint dell’atomo con la velocità
angolare di precessione di Larmor w.
w è proporzionale a Bint.
Bint è dell’ordine del Tesla.
6
Bint
B int
L
-e
Ze
v
J
L

S

-e

Bint
"




'
S
B int
zˆ
zˆ


J
L
S

S




L
Dipolo magnetico di un atomo:
ml= -gl mB/h L
ms= -gs mB/h S
L’interazione spin- orbita (interazione
di tipo magnetico) modifica i livelli
di energia dell’atomo e definisce il
momento angolare totale dell’atomo
J=L+S. Ne segue che il dipolo
magnetico totale dell’atomo
mJ= ml + ms
5