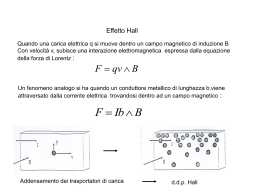
Lezione 9: fenomeni dipendenti dal tempo
Induzione elettromagnetica
In condizioni stazionarie:
 r, J indipendenti dal tempo
 sorgenti

di campo elettrico e magnetico stazionari
 E e B indipendenti l’uno dall’altro
r
E 
0
  B  0 j
B  0
 E  0
In condizioni dinamiche:


 campi E e B non sono indipendenti
 aspetti diversi della stessa entità
campo elettromagnetico
1820 Ørsted: correnti elettriche generano campi magnetici
(elettricità e magnetismo sono collegati)
1831 Faraday: serie di misure sistematiche
 campi magnetici variabili nel tempo
inducono campi elettrici
Osservazioni sperimentali
conseguenza della forza di Lorentz:
magnete produce un campo B verticale
filo (le cariche) si muove orizzontalmente:
 ho una forza di Lorentz F=qvB
 induco una corrente elettrica
(l’effetto è locale, ma la corrente
scorre in tutto il filo)
fenomeno nuovo:
induco una corrente elettrica
in un circuito se:
filo fermo,
magnete in movimento
filo fermo
secondo filo in moto
filo fermo
vario la corrente nel secondo filo

posso indurre corrente in due modi:
campo B stazionario, circuito si muove (flusso tagliato)
circuito fermo, campo B varia nel tempo (flusso concatenato)
N.B.
effetto diretto:
non è l’induzione di una corrente,
ma di una forza elettromotrice:
circuito chiuso  osservo una corrente elettrica
 ho una forza che spinge gli elettroni


F 
f.e.m.    ds
q
=
RI
circuito aperto  non può passare corrente
 misuro differenza di potenziale
d.d.p. viene indotta anche in
circuiti non conduttori !!
Legge di
Faraday - Neumann - Lentz
L’azione della f.e.m. tende ad opporsi a
qualsiasi variazione di campo magnetico
(del flusso del campo magnetico)
d ( B)
f .e.m.  
dt
 
  
f .e.m.   E  dl   (  E )  n ds
l
S
d ( B )
d  

   B  n ds
dt
dt S


B
campo elettrico non conservativo
 E 
(il lavoro per spostare una carica
dt
dipende dal percorso)
lavoro fatto per spostare una
carica si trasforma in una
variazione del campo magnetico
e viceversa.
Flusso tagliato:
la legge di Faraday- Neumann – Lentz
può essere dedotta dalla legge di Lorentz
forza di Lorentz
su elettroni della sbarra
F  IBl

la sbarra si muove con v
Potenza erogata dal generatore:
E0 I  RI 2  Fv
E0
Fv 1
 I0  I 
R
I R
Fv 1
I0  I 
I R
N.B. la massima corrente è
I 0  E0 / R per v=0
 variazione di corrente
causata dalla forza e.m.
Fv
I
IBlv

I
ds
d ( B )
  Bl

dt
dt
f .e.m.  
L’azione della f.e.m. tende ad opporsi a qualsiasi
variazione di campo magnetico
(del flusso del campo magnetico)
Esempio:
anello
conduttore
 bobina attorno ad cilindro di ferro
 anello di rame inserito
attorno al cilindro
l’anello vola via quando chiudo il circuito
su un generatore di corrente alternata !!!!
origine della forza repulsiva:
correnti indotte nell’anello,
si oppongono al cambiamento di B attraverso l’anello
F
 anello e bobina sono equivalenti
a due magneti opposti
S
N
B
N
S
B
taglio l’anello: la forza scompare, non accade nulla
 la forza repulsiva viene dalle correnti!!
Eccezioni
(disco di Barlow)
 disco di rame rotante con velocità v
 magnete in prossimità del disco
 circuito elettrico che collega
centro-estremo del disco
apparentemente non varia nulla:
flusso del campo magnetico è costante
 il circuito è sempre lo stesso
sperimentalmente:
 misuro una corrente elettrica (o una d.d.p.)
tra il centro ed il bordo del disco
il materiale che costituisce
il circuito è in moto
(disco che ruota)
 deve subire la forza
di Lorentz
F  qvB
F  qrB
E
F
 RB
q
R0
1
f .e.m.   RB dr  BR02
2
0
Attenzione ad usare la legge di Faraday quando il
materiale in cui passa la corrente cambia !
Generatore di
corrente alternata
energia cinetica
energia elettrica
B=0
 bobina in rotazione
 campo B uniforme
B0
equivalentemente
S
 bobina fissa
 campo B rotante
  t
 = velocità angolare bobina

 
( B)  B  n S  BS cos  BS cost

d( B)
f .e.m.  
 BS sin t
dt
N.B. f.e.m.  V
se il generatore
non tira corrente !
porto i fili in regione
di spazio in cui
B=0 o B=costante
 
 E  dl  0
I
f .e.m. V0

sin t
R
R
definisco
potenziale elettrico
V  BS  sin t  V0 sin t
f.e.m.
(B)
Alternatore
Superconduttori
(Conduttori Perfetti)
circuito superconduttore:
una corrente I:
circola all’infinito;
 non si hanno effetti dissipativi.
 una f.e.m. (anche molto piccola):
 genera una corrente infinita
I = V/R  R=0

I=
non è possibile indurre una f.e.m.
non posso far variare il flusso di B
in un materiale superconduttore non sarò mai in grado
di far entrare delle linee di campo magnetico:
 il superconduttore crea delle
correnti indotte con f.e.m. infinitesima
ottimo schermo magnetico
Levitazione Magnetica
in superconduttori
magnete in prossimità di un superconduttore:
si inducono correnti circolari
all’interno del superconduttore
tale da creare un
controcampo magnetico
che respinge il magnete stesso
se il superconduttore è curvato
a forma di scodella il magnete
resta sospeso
N.B. non esistono materiali ordinari superconduttori
a temperatura ambiente.
T=3.80K Sn è superconduttore
Correnti di Spostamento



B
 E 
dt



  B  0 J
vale solo in regime stazionario


div (  B )  0

r
equazione di continuità  div J  
0
t
contraddizione
1
 
 

 (  B)  d   B  ds   0 I
1

 
 

0   (  B )  d   B  ds
2
2




legge della circuitazione 
E
  B  0 J   0 0
di Ampere-Maxwell
t




 (divE )
div (  B)   0 divJ   0  0
0
t

( r /  0 )
div J   0
0
t
In forma integrale:
 
 

d  
 B  ds   (  B)  d 0 I conc  0 0 dt  E d

corrente
d ( E )
  0 I conc   0 0
di spostamento
dt
Verifica sperimentale:
2
1
 solenoide toriodale tra le armature di un condensatore
condensatore alimentato da f.e.m. variabile
 campo E variabile nel condensatore
 campo B varia nel tempo
 (B) concatenato al solenoide varia nel tempo
f.e.m. indotta nel solenoide in posizione 1
(originata da d(B)/dt)
=
f.e.m. indotta nel solenoide in posizione 2
(originata da I(t))
Considerazioni di Maxwell
E=0
coppia di armature
con materiale isolante
se E=0
baricentro +  baricentro 
E0
se E0
baricentro +  baricentro 
 impulso di corrente
corrente di spostamento
(dura fino a che le molecole
hanno raggiunto equilibrio)
corrente impulsiva
I
un campo elettrico variabile
induce un campo magnetico
E0
linee di B associato ad I
Conservazione della carica
evidenza sperimentale:
 la carica elettrica si conserva
 per ogni carica positiva creata
si crea carica negativa uguale
Q
dQ

 I
dt
 
dQ

  j  n dS
S
dt
d

dt

V
rdV   
V
r
dV 
t

r
 j  
t
V
S
I

V

  j dV
equazione di
continuità
conservazione locale della carica;
piu` forte della conservazione globale
(esempio: diminuisco di 1C la carica a Milano
aumento di 1C la carica a Parigi!!)
Forza elettromagnetica
forza di cui risente una particella
di carica q
con velocità v
in presenza di campi
elettrici e magnetici
(costanti o variabili)
forza su carica in quiete:
può essere generata da:
anisotropia
di carica elettrica
campo magnetico
variabile
(

  
F  q EvB

qE

E
forza
elettrostatica
q1q2 
r
3
40 r


B
 E  
t
1
 
forza su una carica in moto: qv  B
 non esiste una forza ‘nuova’
indotta da campi magnetici variabili
campo elettrostatico e magnetostatico
sono intimamente legati tra loro
)