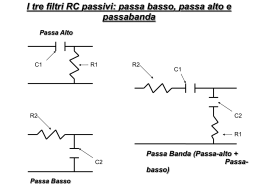
RIEPILOGO
Filtri del secondo ordine e
diagrammi di Bode
SUMMARY
Second order filters and Bode plots
Filtri del secondo ordine
» I filtri L-C e C-L sono filtri del secondo
ordine.
» L-C and C-L filters are the second-order
filters.
Caduta di tensione
» I filtri L-C passa-basso sono impiegati soprattutto
quando desideriamo limitare la caduta di tensione
dovuta alla corrente continua che avverrebbe sulla
resistenza in serie di un filtro R-C.
» The L-C low-pass filters are used especially when
we want to limit the voltage drop due to the
current that would take place on series resistance
of an R-C filter.
Circuito risonante serie
» Il filtro L-C passa-basso è un circuito risonante serie.
Le espressioni del guadagno e della frequenza di
risonanza sono:
G ( j ) 
20
j R
  
L
2
0
2
0 
1
LC
» The L-C low-pass filter is a series resonant circuit. The
expressions of the gain and resonance frequency are:
G ( j ) 
20
20  2 
j R
L
0 
1
LC
Coefficiente di risonanza
»
L’altezza e la forma del picco di risonanza sono determinati dal valore del
coefficiente di risonanza Q. Per i nostri scopi l’usuale definizione di Q è
il rapporto tra la frequenza di risonanza e l’ampiezza di banda presa
quando la potenza si dimezza:

f
f
Q 0  0  0
2  2 f
B
dove f0 è la frequenza di picco.
»
The height and shape of the resonance peak are determined by the value
of the coefficient of resonance Q. For our purposes the usual definition of
Q is the ratio between the resonance frequency and
the bandwidth taken when the power is halved:

f
f
Q 0  0  0
2  2 f
B
where f0 is the peak frequency.
Connessione in cascata
» I filtri del secondo ordine possono essere
anche ottenuti connettendo in cascata
due filtri del primo ordine.
» The filters of the second order can be also
obtained by connecting in cascade two
filters of the first order.
Pendenza della curva
» Connettendo in cascata un numero n di filtri
del primo ordine otteniamo un filtro di ordine
n con una pendenza della curva di risposta
pari a n ∙ 20 dB/decade.
» Connecting in cascade a number n of filters of
the first order we obtain a filter of order n
with a slope of the response curve equal to
n ∙ 20 dB/decade.
Curva di risposta
» La curva di risposta di un filtro passa-banda
può essere immaginata come una curva
derivante dal risultato della messa in cascata (il
prodotto) di un passa-alto e di un passa-basso.
» The response curve of a band-pass filter can
be imagined as a curve derived from the result
of the putting in cascade (the product) of a
high-pass and a low-pass.
Filtro passa-banda
» Un circuito risonante R-L-C serie o parallelo può costituire
un filtro passa-banda. In quelli serie otteniamo un
passa banda quando l’uscita è presa ai capi del resistore,
oppure un filtro respingi-banda quando l’uscita è presa ai
capi delle serie L-C.
» A series or parallel R-L-C resonant circuit can constitute a
band-pass filter. In those series we get a band-pass
when the output is taken across the resistor, or a bandreject filter when the output is taken across the L-C.
Banda passante
» Per la banda passante di un circuito risonante
R-L-C, vale la relazione:
f0
R
B  f2  f1 

2L Q
» For the bandwidth of a resonant circuit R-L-C,
the following relation holds:
f0
R
B  f2  f1 

2L Q
Teorema della risposta in frequenza
»
Il teorema della risposta in frequenza stabilisce che, per un sistema lineare avente
funzione di trasferimento G(jω), se applichiamo al suo ingresso un segnale sinusoidale di
pulsazione ω0, alla sua uscita a regime è presente un segnale sinusoidale avente:
- stessa pulsazione;
- ampiezza pari al prodotto del modulo del segnale per il modulo di G(jω) calcolata alla
pulsazione ω0;
- fase pari alla somma di quella del segnale d’ingresso con quella di G(jω) calcolata alla
pulsazione ω0.
»
The frequency response theorem states that, for a linear system, whose transfer
function is G(jω), if we apply a sinusoidal signal with pulse ω0 at its input, to its output in
steady-state there is a sinusoidal signal having :
- same pulsation;
- amplitude equal to the product of the signal for the module of G(jω) calculated to the
pulsation ω0;
- phase equal to the sum of that of the input signal with that of G(jω) calculated to the
pulsation ω0.