Corso di Informatica
(Basi di Dati)
Lezione 3 (19 dicembre 2008)
Modello Entità-Relazione:
cardinalità delle relazioni, identificatori
e generalizzazioni
Da:
Atzeni, Ceri, Paraboschi, Torlone - Basi di Dati
Lucidi del Corso di Basi di Dati 1, Prof. Carlo Batini, Laurea in Informatica,
AA 2007-2008
1
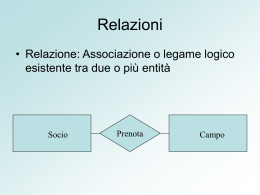
Il modello Entità-Relazione
Il modello Entità-Relazione (modello ER) è un modello concettuale che fornisce
una serie di costrutti per descrivere lo
schema della realtà di interesse in
maniera indipendente da come poi i
relativi dati saranno organizzati
sull’elaboratore, cioè indipendentemente
dal modello logico e dal modello fisico.
2
I costrutti del modello E-R
I costrutti del modello E-R sono:
 Entità
 Attributi di Entità
 Relazione
 Attributi di Relazione
 Cardinalità di Relazione
 Identificatori
 Generalizzazioni
3
La cardinalità delle relazioni
Data un’entità E coinvolta in una relazione R
(di grado qualsiasi), il vincolo di cardinalità
esprime il numero minimo m (cardinalità
minima) e il numero massimo M (cardinalità
massima) di occorrenze (istanze) di R a cui
un’occorrenza (istanza) di E può partecipare.
Graficamente si ha:
E
(m,M)
R
...
4
La cardinalità delle relazioni
Nel seguito si farà riferimento a relazioni di
grado 2 (relazioni binarie) che coinvolgono
quindi due sole entità.
Un esempio che meglio chiarisce il concetto in
questione è il seguente. Si consideri lo schema:
Impiegato
(1,5)
Assegnazione
(0,50)
Progetto
Le entità Impiegato e Progetto sono legate dalla
relazione Assegnazione. Si vuole infatti modellare,
per la realtà azienda, il fatto che ogni impiegato sia...5
La cardinalità delle relazioni
…coinvolto in progetti. Un’occorrenza della relazione
Assegnazione è una coppia (I, P), dove I è
un’occorrenza dell’entità Impiegato e P
un’occorrenza dell’entità Progetto. Cioè
all’impiegato I è stato assegnato il progetto P. Il fatto
che il vincolo di cardinalità per Impiegato in
Assegnazione sia (1,5), significa che un’occorrenza di
Impiegato può partecipare da un minimo di 1 volta ad
un massimo di 5 volte ad una occorrenza di
Assegnazione. In altre parole nella realtà modellata
dallo schema precedente, ad un impiegato deve
obbligatoriamente essere assegnato almeno un
progetto ma non gli possono essere assegnati più... 6
La cardinalità delle relazioni
…di 5 progetti.
Allo stesso modo possiamo dire che un’occorrenza
dell’entità Progetto può partecipare da un minimo di
0 volte ad un massimo di 50 volte ad una occorrenza
di Assegnazione. Quindi un progetto può anche non
essere assegnato a nessun impiegato (ad esempio un
progetto lanciato da poco tempo) e non può essere
assegnato a più di 50 impiegati. Si considerino le
seguenti istanze di Impiegato, Progetto e
Assegnazione:
Impiegato -> {I1, I2, I3}
Progetto -> {P1, P2, P3, P4, P5}
Assegnazione -> {(I1, P1),(I2, P4),(I3, P2),(I1, P4),(I1, P5),(I3, P5)}7
La cardinalità delle relazioni
…Si può notare che:
 a tutti gli impiegati è assegnato almeno un
progetto e non più di 5 progetti
 tutti i progetti sono assegnati a non più di 50
impiegati (il progetto P3 non è assegnato a nessuno)
In definitiva l’insieme delle occorenze della relazione
Assegnazione della slide precedente rispetta il
vincolo di cardinalità evidenziato nello schema.
8
La cardinalità delle relazioni
I valori maggiormente utilizzati per la cardinalità
minima sono:
 0, significa che la partecipazione è opzionale
 1, significa che la partecipazione è obbligatoria
Nello schema:
Impiegato
(1,5)
Assegnazione
(0,50)
Progetto
9
La cardinalità delle relazioni
…la partecipazione dell’entità Impiegato alla
relazione Assegnazione è obbligatoria, ovvero un
impiegato deve obbligatoriamente essere
coinvolto in un progetto. La partecipazione dell’entità
Progetto alla relazione Assegnazione è invece
opzionale, ovvero un progetto può anche
non essere assegnato a nessun impiegato.
10
La cardinalità delle relazioni
I valori maggiormente utilizzati per la cardinalità
massima sono:
 1, significa che le occorrenze dell’entità
partecipano al più 1 volta alle occorrenze della
relazione
 N, significa che le occorrenze dell’entità
partecipano un qualsivoglia numero di volte alle
occorrenze della relazione
11
La cardinalità delle relazioni
Si consideri ad esempio il nuovo schema:
Impiegato
(1,5)
Assegnazione
(0,N)
Progetto
La differenza con lo schema precedente (in cui la
cardinalità massima di Progetto era 50) è che ora
un’occorrenza di Progetto può partecipare ad un
numero qualsiasi di occorrenze di Assegnazione (non
più limitato a 50).
12
La cardinalità delle relazioni
Si consideri ora il nuovo schema:
Impiegato
(1,1)
Assegnazione
(0,N)
Progetto
In questo caso, rispetto allo schema precedente,
si è portata a 1 la cardinalità massima di Impiegato
in quanto si vuole modellare il fatto che
un’occorrenza di Impiegato può partecipare ad una
sola occorrenza della relazione Assegnazione.
In altre parole un impiegato deve essere coinvolto
obbligatoriamente in un solo progetto.
13
La cardinalità delle relazioni
...Si noti che la coppia (0, N) per le cardinalità
minima e massima di un’entità in una relazione
è equivalente all’assenza del vincolo di cardinalità.
Nello schema precedente, infatti un progetto può
essere assegnato a 0 o ad un qualsivoglia numero di
impiegati.
14
Esempi di vincolo cardinalità
Si consideri il seguente schema:
Persona
(0,N)
Residenza
(0,N)
Città
Potrebbe essere compatibile con la realtà
amministrativa italiana?
NO, perché non è ammesso che una persona in Italia
abbia più città di residenza.
15
Esempi di vincolo cardinalità
Si consideri quest’altro schema:
Persona
(0,1)
Residenza
(0,N)
Città
Potrebbe essere compatibile con la realtà
amministrativa italiana?
SI’, se ammettiamo che non è necessario che la
residenza di un impiegato sia nota (se però è nota
questa è unica)
16
Esempi di vincolo cardinalità
Si consideri quest’altro schema:
Persona
(1,1)
Residenza
(0,N)
Città
Potrebbe essere compatibile con la realtà
amministrativa italiana?
SI’, se ammettiamo che è necessario che la
residenza di un impiegato sia nota è unica
17
Classificazione delle
relazioni binarie
Una relazione R tra due entità E1 ed E2 (grado 2)
E1
(m1,M1)
R
(m2,M2)
E2
Viene classificata, sulla base dei valori delle
cardinalità massime M1 e M2, in:
 relazione “uno a uno” se M1= M2=1
 relazione “uno a molti” se M1=1 e M2=N
relazione “molti a molti” se M1=N e M2=N
18
Classificazione delle
relazioni binarie
Esempi di relazioni binarie “uno a uno”
Impiegato
Professore
(0,1)
(1,1)
Direzione
Docenza
(1,1)
(1,1)
Progetto
Corso
19
Classificazione delle
relazioni binarie
Esempi di relazioni binarie “uno a molti”
Studente
Comune
(1,1)
(1,1)
Nascita
Ubicazione
(0,N)
(1,N)
Città
Provincia
20
Classificazione delle
relazioni binarie
Esempi di relazioni binarie “molti a molti”
Studente
Montagna
(0,N)
(0,N)
Esame
Scalata
(0,N)
(1,N)
Corso
Alpinista
21
Gli identificatori di entità
Un identificatore di entità è un insieme di
proprietà che identificano univocamente le
istanze dell’entità. Cioè non possono esistere
due istanze dell’entità che assumono lo
stesso valore per tutte le proprietà che
formano l’identificatore.
Nel seguito ci occuperemo solo di
identificatori interni (composti solo da
attributi di entità).
Su ogni entità deve essere definito almeno
22
un identificatore.
Gli identificatori di entità
Si consideri il seguente schema in cui l’entità
Persona ha i seguenti attributi: Codice
fiscale, Cognome, Nome, Residenza.
Cod.Fis.
Cognome
Persona
Nome
Residenza
L’identificatore per Persona può essere
Codice Fiscale (unico attributo)
23
Gli identificatori di entità
Oppure il seguente schema in cui l’entità
Persona ha i seguenti attributi: Cognome,
Nome, Data di nascita, Residenza
Cognome Nome
Persona
Data di nascita
Residenza
L’identificatore per Persona può essere
(Cognome,Nome,Data di Nascita) (tre
attributi)
24
Gli identificatori di entità
Oppure il seguente schema in cui l’entità
Automobile ha i seguenti attributi: Targa,
Modello, Colore.
Targa
Modello
Colore
Automobile
L’identificatore per Automobile può essere
Targa (unico attributo)
25
Gli identificatori di entità
Oppure il seguente schema in cui l’entità
Persona ha i seguenti attributi: Cognome,
Nome, Data di nascita, Residenza
Cognome Nome
Persona
Data di nascita
Residenza
L’identificatore per Persona può essere
(Cognome,Nome,Data di Nascita) (tre
attributi)
26
Gli identificatori di entità
Per un’entità, l’insieme di tutti i suoi
attributi costituisce banalmente un
identificatore in quanto si suppone che non
possano esistere due occorrenze
completamente coincidenti.
27
Gli identificatori di entità
La rapresentazione grafica di un
identificatore composto da un solo attributo
è l’annerimento del corrispondente pallino
Cod.Fis.
Cognome
Persona
Nome
Residenza
28
Gli identificatori di entità
La rapresentazione grafica di un
identificatore composto da più attributi
è una linea che unisce gli attributi e che
termina con un pallino annerito
Cognome Nome
Persona
Data di nascita
Residenza
29
Le generalizzazioni
Un’entità E più generale, rispetto ad un
unico criterio, di n entità E1, E2, …, En, è detta
generalizzazione di E1, E2, …, En. Le
n entità sono dunque specializzazioni di E.
E è detta entità padre ed E1, E2, …, En sono
dette entità figlie (o sottoentità).
Ad esempio le entità Uomo e Donna sono
specializzazioni dell’entità Persona che è
a quindi una generalizzazione di Uomo e
Donna.
30
Le generalizzazioni
La rappresentazione grafica di una
generalizzazione è un arco che collega le
entità figlie tra di loro e una freccia che
collega l’arco all’entità padre
Persona
Uomo
Donna
31
Le generalizzazioni
Valgono le seguenti proprietà:
 ogni occorrenza di un’entità figlia e anche
occorrenza dell’entità padre
 ogni proprietà dell’entità padre (attributi,
identificatori, relazioni e altre
generalizzazioni) è anche proprietà delle
entità figlie -> ereditarietà
32
Le generalizzazioni
Cognome Nome
Matricola
Studente
Data di nascita
Persona
Docente
Ogni attributo di Persona è ereditato da Studente
e in più Studente ha l’attributo Matricola
33
Le generalizzazioni
Una generalizzazione è:
 totale se ogni occorrenza dell’entità padre
è un’occorrenza di almeno una delle entità
figlie, altrimenti è parziale
 esclusiva se ogni occorrenza dell’entità padre
è al più un’occorrenza di una delle entità
figlie, altrimenti è sovrapposta
34
Le generalizzazioni
Esempio di generalizzazione totale
ed esclusiva:
Persona
Uomo
Donna
35
Le generalizzazioni
Esempio di generalizzazione parziale
ed esclusiva:
Persona
Studente
Docente
36
Le generalizzazioni
Esempio di generalizzazione parziale
e sovrapposta:
Persona
Studente
Impiegato
37
Le generalizzazioni
La stessa entità può essere padre in distinte
generalizzazioni
Persona
Uomo
Donna
Studente
Docente
Le due generalizzazioni corrispondono a due criteri diversi
38
di classificazione dell’occorrenze dell’entità padre Persona