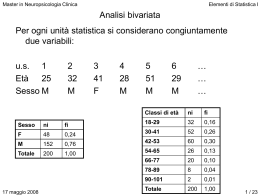
Master in Neuropsicologia Clinica
Elementi di Statistica I
Repetita iuvant
• Rappresentazioni grafiche var. qualitative (barre, torta)
• Sintesi di variabili quantitative:
– Min, max
– Media, proprietà:
• Internalità
• Baricentro
• Linearità
• Minimizzazione somma quadrati scarti
i (xi – )2  i (xi – )2 per qualsiasi 
– Media ponderata
19 aprile 2008
1 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
Variabilità per variabili quantitative
1.
campo di variazione: max(Xi) – min(Xi)
2.
scarto interquartile:
a) quartili:
19 aprile 2008
mediana
quartili
→
→
Q1 →
valore associato all’unità ordinata che
viene dopo il primo 25%
Q2 →
valore associato all’unità ordinata che
viene dopo il primo 50% (Mediana!!!)
2 parti uguali
4 parti uguali
2 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
Q3 →
valore associato all’unità ordinata che
viene dopo il primo 75%
Q4 →
valore associato all’unità ordinata che
viene dopo il primo 100% (Max!!!)
in pratica:
I. si ordinano le unità
II. si individuano le unità portatrici di Q1 e Q3:
i. Q1 = x((n+1)/4)
ii. Q3 = x((n+1)3/4)
N.b. il quartile, come la mediana, non è la posizione
bensì la modalità associata alla posizione!
19 aprile 2008
3 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
III. se le posizioni non sono un numero intero?
i.
si considera la parte intera separata da quella decimale:
Es.: n = 29 → (n + 1)/4 = 30/4 = 7,5
→
parte intera c1 = [(n + 1)/4]
7
parte decimale d1 = (n + 1)/4 – [(n + 1)/4] → 0,5
Q1 = x(c1) + d1(x(c1+1) – x(c1)) =
= x(7) + 0,5(x(8) – x(7)) = 18
Totale
19 aprile 2008
Età
ni
fi
Ni
Fi
18
10
0,345
10
0,345
19
3
0,104
13
0,449
20
7
0,241
20
0,690
21
9
0,310
29
1,000
29
1,000
4 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
→ (n + 1)3/4 = 90/4 = 22,5
parte intera c3
→
22
parte decimale d3
→
0,5
Q3 = x(c3) + d3(x(c3+1) – x(c3)) =
= x(22) + 0,5(x(23) – x(22)) = 21
Totale
19 aprile 2008
Età
ni
fi
Ni
Fi
18
10
0,345
10
0,345
19
3
0,104
13
0,449
20
7
0,241
20
0,690
21
9
0,310
29
1,000
29
1,000
5 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
b) scarto interquartile: Q = Q3 – Q1
osservazioni:
– lo scarto interquartile individua il range del 50% della distribuzione
centrata sulla mediana (il secondo quartile…)
u.s.
modalità
(posizione)
2
3 4 …
… 4
8 14 …
… 26
18 18 18 …
… 20 20 20 …
(1) (2) (3) …
…(14) (15) (16)…
25%
… 21
Q2
Q3
18
20
21
25%
29
21
… (27) (28)
Q1
25%
27
21
(29)
25%
50%
19 aprile 2008
– maggiore è Q, maggiore sarà la dispersione
6 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
scarto quadratico medio σ:
3.
scarto: (xi – μ)
n
  xi   
quadratico:
2
i 1
n
n
  xi   
medio:
2
i (xi – )2  i (xi – )2
per qualsiasi 
i 1
nn
n

  xi  x 
i 1
n

19  19,5  18  19,5  18  19,5
2

2
19 aprile 2008
2
29
2
 ...   21  19,5 
2
 1, 25
7 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
osservazioni:
−
è nella stessa unità di misura dei dati (dipende dall’ordine di grandezza)

circa il 70% dei valori osservati dovrebbe cadere nell’intervallo μ ± σ

σ≥0

σ = 0 → omogeneità
n


 x  
i 1
2
i
n
__
2
 x  2
__
2
  x   2  382, 482  380,913  1, 25
−
se si hanno le distribuzioni di frequenze lo sqm diventa:
n

19 aprile 2008
2

xi  x  ni 




i 1
n
n
2

   xi  x  fi 


i 1
8 / 17
Master in Neuropsicologia Clinica
4.
Elementi di Statistica I
varianza σ2:
quadrato dello sqm…
n
2 
  xi  x 
2
i 1
n
osservazioni:
 non è nella stessa unità di misura dei dati bensì il suo quadrato





(dipende dall’ordine di grandezza)
σ2 ≥ 0
σ2 = 0__ omogeneità
 2  x2   2
poco informativa nell’analisi monovariata
se si hanno le distribuzioni di frequenze :
n
 
2
19 aprile 2008
2

x

x
ni 



i


i 1
n
n
2
   xi  x  fi 


i 1
9 / 17
Master in Neuropsicologia Clinica
n
2 
  xi  x 
i 1
n
Elementi di Statistica I
2

19  19,5  18  19,5   18  19,5 


2
2
2
 ...   21  19,5 
2
29
sigarette/h
ni
Età
ni
1
6
18
10
2
15
19
3
3
5
20
7
4
3
21
9
totale
29
Totale
 1,56
29
qual è la variabile che presenta maggiore variabilità?
σetà = 1,249
19 aprile 2008
σsig =
10 / 17
Master in Neuropsicologia Clinica
ni
xini
xi2
xi2ni
1
6
6
1
6
2
15
30
4
60
3
5
15
9
45
4
3
12
16
48
29
63
159
2,172
5,483
sigarette/h
Tot
Media
Elementi di Statistica I
σ
0,875
__
2
  x  x2
m
x
i i
i 1
n
m
__
2
x 
σetà = 1,249
xn
2
x
 i ni
i 1
n
σsig = 0,875
ordini di grandezza differenti, unità di misura diverse,
appartenenza a gruppi di numerosità differente…
→ confronto?
19 aprile 2008
11 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
coefficiente di variazione (CV):
X
CVX 

→ numero puro!
19 aprile 2008
sig/h
Età
18
180
σ
0,875
1,249
18
180
Media
2,172
19,517
20
200
CV
0,403
0,064
21
210
22
220
17
170
15
150
σ
2,429972
24,29972
σ2
5,904764
590,4764
12 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
Raggruppamento in classi
Esigenze di sintesi rendono oneroso e di poca rilevanza
elencare tutte le modalità con rispettive frequenze
modalità
→
intervalli di valori
→
classi
Es.:
•
•
•
•
19 aprile 2008
u.s.: paziente
variabile: età
unità di misura: anni
numerosità gruppo: 1738
13 / 17
15
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
89
91
92
94
95
96
97
99
Master in Neuropsicologia Clinica
ni
19 aprile 2008
Elementi di Statistica I
età
ni
15
1
17
7
18
18
19
18
…
…
97
1
99
1
Totale 1738
70
60
50
40
30
20
10
0
Età
14 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
classe: intervallo di valori entro il quale si distribuiscono le
osservazioni
• procedura (semplificata):
–
si determina il range: r = max – min
–
si sceglie il numero di classi = k
–
si divide il range (r* un po’ più ampio di quello
calcolato) per il numero di classi → si ottiene
l’ampiezza di ogni classe d
–
1° classe:
inf < min
sup = est. inf. + d
2° classe:
inf. = sup.1° + 1
sup. = est. inf. + d
ecc...
19 aprile 2008
15 / 17
Master in Neuropsicologia Clinica
•
•
•
•
•
•
•
•
Elementi di Statistica I
min=15
max=99
r=84
k=4
r*=88
d=r*/k=22
1° classe : inf = 14
2° classe : inf = 36+1=37
→
→
sup = 14+22=36
sup = 37+22=59
Classi di
Età
19 aprile 2008
inf
sup
14
36
37
59
60
82
83
105
16 / 17
Master in Neuropsicologia Clinica
Elementi di Statistica I
→ distribuzione di frequenze per le classi...
Classi di
età
ni
fi
Ni
Fi
14-36
571
0,328
571
0,328
37-59
821
0,472
1392
0,800
60-82
333
0,192
1725
0,992
83-105
13
0,008
1738
1,000
Totale
1738
1,000
osservazioni:
•
è più conveniente considerare ampiezze costanti
•
da tale distribuzione non è possibile identificare
la reale distribuzione originaria…
19 aprile 2008
17 / 17