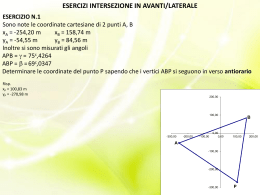
CELERIMENSURA
Il rilievo topografico ha lo scopo di determinare,
CRITERI
mediante misure, la posizione completa dei punti
ORGANIZZATIVI
DEI RILIEVI
individuati sul terreno, calcolandone le coordinate
plano - altimetriche X, Y, Z (Q)
I punti necessari a definire una rappresentazione
cartografica, che costituisce lo scopo primario di un
rilievo topografico, possono essere distinti in due
categorie:
DIFFERENZE TRA I
PUNTI RILEVATI
punti di inquadramento o di appoggio
punti di dettaglio
I punti di inquadramento o di appoggio, ad
esempio i PF, sono solo una piccolissima
percentuale dei punti rilevati e la loro
posizione
PUNTI DI
INQUADRAMENTO
O DI APPOGGIO
viene
definita
mediante
le
operazioni topografiche di triangolazione,
intersezione e poligonazione. Questi punti
costituiscono il punto di partenza per il
rilievo
dei
particolari
topografici
permettono la descrizione del territorio
che
La posizione dei punti di dettaglio, che costituiscono
la grande maggioranza dei punti rilevati, si ottiene
collegandoli con misure angolari o lineari ad uno o più
punti della rete di inquadramento.
PUNTI DI
I metodi di rilievo utilizzati per determinare la
DETTAGLIO
posizione
di
questi
punti
sono
numerosi,
ma
l’evoluzione degli strumenti impiegati ha determinato
una selezione degli stessi, a seguito della quale pochi
di questi trovano effettivo impiego pratico nella
pratica professionale
Tra i metodi che utilizzano tecnologie tradizionali, di fatto il
metodo più utilizzato nel rilievo dei particolari, per la
rapidità e la semplicità operativa, è quello per coordinate
polari (o irradiamento). Con esso, di ciascun punto rilevato
METODI DI
RILIEVO
vengono misurate, dalla stazione di partenza la distanza e la
direzione (azimut o angolo al vertice)
A questo metodo tradizionale, si sono affiancati di recente,
metodi cinematici, legati al posizionamento satellitare GPS,
come il metodo stop and go
Rilievo per coordinate polari dalle
PF17
stazioni 600 e 700 appoggiato a
due poligonali collegate a PF
100
200
703
601
702
METODI DI
RILIEVO
500
701
602
600
300
603
700
604
400
PF02
PF11
La scelta dei punti da rilevare viene fatta dopo aver
eseguito una attenta ricognizione sul territorio. Dei punti
scelti viene redatta una apposita monografia corredata da
schizzo grafico o fotografia
I punti devono essere successivamente identificati. La
IDENTIFICAZIONE
DEI PUNTI
scelta più semplice è quella di tipo numerico con andamento
progressivo, ma può essere convenientemente adottata
solo per pochi punti. In caso contrario, pur mantenendosi
una numerazione progressiva questa è collegata al nome
della stazione da cui i punti sono stati rilevati. Il nome
della stazione è sempre multiplo di 100
Il rilievo dei particolari implica in via preliminare,
come si è detto, una rete di appoggio o di
inquadramento. Tale rete, è costituita generalmente
da poligonali chiuse o aperte meglio se vincolate. Se
SUPPORTO AL
RILIEVO DEI
PARTICOLARI
la zona da rilevare è molto piccola, la rete di
inquadramento può ridursi ad una sola poligonale e nei
casi più semplici a pochissimi punti di posizione nota
collegati alla stazione ( ad esempio un triangolo
fiduciale previsto dalla normativa catastale per gli
atti geometrici di aggiornamento)
Il criterio fondamentale della CELERIMENSURA è
quello di abbinare contemporaneamente al rilievo
planimetrico per coordinate polari, una livellazione
che permetta di determinare il dislivello tra la
RILIEVO PLANO
ALTIMETRICO DEI
PARTICOLARI
LA CELERIMENSURA
stazione e il punto considerato. Nota la quota di un
punto è possibile successivamente calcolare le quote
di tutti gli altri punti
Con la misura delle distanze, degli angoli orizzontali e
verticali e dei dislivelli è quindi possibile calcolare le
coordinate X, Y, Z (Q) di ogni punto rilevato
Se del punto di stazione sono note le
coordinate plano altimetriche è possibile
mediante una semplice somma algebrica
RILIEVO PLANO
ALTIMETRICO DEI
calcolare le coordinate totali di tutti i
PARTICOLARI
LA CELERIMENSURA
punti rilevati rispetto allo stesso sistema
di riferimento a cui sono riferite le
coordinate del punto di stazione (vale per i
sistemi locali o orientati)
Fu Ignazio PORRO,
PORRO che dopo la seconda metà del XIX secolo,
ebbe per primo l’idea di razionalizzare le tecniche di rilievo
topografico considerando contemporaneamente sia l’aspetto
planimetrico che quello altimetrico. Egli propose una nuova
tecnica operativa di rilievo di dettaglio, poi universalmente
adottata, che chiamò CELERIMENSURA per mezzo della quale
IGNAZIO PORRO
venne eseguita buona parte dei lavori cartografici in tutto il
mondo fino all’affermarsi della fotogrammetria aerea
Ignazio PORRO concepì anche lo strumento idoneo alla tecnica
di rilievo da lui inventata. Tale strumento era il CLEPS,
CLEPS il
primo
strumento
con
i
cerchi
tacheometri e delle stazioni totali
protetti,
antenato
dei
CLEPS E
TACHEOMETRI
Tacheometro ottico meccanico che
permette la misura diretta degli
angoli orizzontali e verticali e la
misura indiretta della distanza
Asta metrica in legno o
acciaio alta 4 o 5 metri
LA STADIA VERTICALE
fs
UTILIZZATA PER LA
MISURA INDIRETTA
DELLA DISTANZA
fm = (fs + fi)/2
fm
fi
x
φ
S
S = (ls – li)
x
ls
li
h
B
DISTANZA INDIRETTA
CON TACHEOMETRO E
STADIA VERTICALE
x
A
D
x
D = K x S x sen2 φ = K x (ls – li) x sen2 φ
K = 100 = costante
se φ = 100c, cann. orizzontale risulta sen2 φ = 1, da cui
S = (ls – li) = intervallo di stadia
D = K x S = K x (ls – li)
φ = angolo verticale
φ
x
lm
h
B
x
LIVELLAZIONE
TACHEOMETRICA
∆AB
x
A
D
∆AB = D x cotg φ + h – lm
se φ = 100c allora cotg φ = 0
∆AB = h – lm
quest’ultima formula corrisponde ad una livellazione
geometrica da un estremo
x
Utilizzando nel rilievo un tacheometro con stadia
verticale le coordinate plano altimetriche di un punto
B riferite al punto di stazione A, si ottengono dalle
tre relazioni
CALCOLO DELLE
COORDINATE DI UN
XB = XA + D x sen (AB) = XA + K x S x sen2 φ x sen (AB)
PUNTO CON
TACHEOMETRO E
STADIA VERTICALE
YB = YA + D x cos (AB) = YA + K x S x sen2 φ x cos (AB)
QB = QA + D x cotg φ + h – lm = QA + K x S x sen φ x cos φ + h - lm
Le grandezze misurate per ciascun punto collimato cioè
S = (ls – li), lm, h, φ, ... si chiamano numeri generatori
B
Y
∆AB
xB
yB
Y’
A
xA
QB
QA
CALCOLO DELLE TRE
B’
COORDINATE DEL
PUNTO B
2
(AB)
A’
yA
n
x se
S
K x
D =
φ
XB = XA + D x sen (AB) = XA + K x S x sen2 φ x sen (AB)
YB = YA + D x cos (AB) = YA + K x S x sen2 φ x cos (AB)
QB = QA + ∆AB = QA + D x cotg φ + h - lm
X
π
STAZ.
PUNTI
C.O.
C.V.
Fs
Fm
Fi
1
0C.0000
102C.000
2.157
1.705
1.253
2
51C.3600
100C
1.936
1.529
1.122
3
92C.4800
100C
2.228
1.800
1.372
B
108C.130
100C.920
1.976
1.474
0.972
4
302C.130
97C.1600
1.283
1.198
1.113
A
308C.130
----
----
----
----
B
5
312C.450
108C.130
2.145
1.905
----
hB =
6
336C.220
108C.130
----
----
----
7
354C.790
108C.130
----
----
----
A
hA =
IL LIBRETTO DI
CAMPAGNA
SE SI UTILIZZA IL
TACHEOMETRO E LA
PART. 81
1
STADIA VERTICALE
2
6
7
B
3
A
4
(AB) = 108C.13
5
c .92
n2 100
2) x se
7
.9
0
.976 –
0 x (1
AB =10
38 m
= 100.
(BA) = 308C.13
La
stazione
tacheometri
totale
ottico
evoluzione
–
dei
meccanici,
permette la misura diretta degli angoli e
della
distanza
D
(orizzontale
o
inclinata). Note le coordinate plano
altimetriche del punto di stazione o di
STAZIONI TOTALI
E MIRE
un altro punto collimato permette il
calcolo immediato delle coordinate di
tutti i punti rilevati
D
x
x
φ
X
Dr
x
hp
hs
B
x
DISTANZA E
DISLIVELLO CON
∆AB
STAZIONE TOTALE
E PRISMA
x
A
D
x
Misurando la distanza reale Dr e
Per il dislivello ∆AB osservando che
l’angolo verticale la distanza
hs + X = ∆AB + hp
orizzontale D si ottiene dalla
si ottiene
D = Dr x sen φ
∆AB = hs – hp + X = hs – hp + Dr x cos φ
Utilizzando nel rilievo una stazione totale posta nella stazione A
e un prisma posto nel punto B le coordinate si ottengono dalle
relazioni
XB = XA + D x sen (AB)
CALCOLO DELLE
COORDINATE DI UN
YB = YA + D x cos (AB)
PUNTO CON
STAZIONE TOTALE E
PRISMA
QB = QA + ∆AB = QA + Dr x cos φ + hs - hp
Se φ = 100C cannocchiale orizzontale allora:
sen φ = 1 e cos φ = 0 da cui:
D = Dr
e
∆AB = hs - hp
PART. 81
1
2
6
7
B
3
5
IL LIBRETTO DI
CAMPAGNA
A
(AB) = 108C.13
SE SI UTILIZZA LA
STAZIONE TOTALE
CON IL PRISMA
(BA) = 308C.13
4
STAZ.
A
hA = 1.480
B
hB = 1.510
PUNTI
C.O.
C.V.
DIST.
hP
1
0C.0000
102C.0000
70.150
1.705
2
51C.3600
100C
51.280
1.529
3
92C.4800
100C
45.420
1.800
B
108C.1300
100C.9200
93.100
1.474
4
302C.1300
97C.1600
32.710
1.198
A
308C.1300
----
----
----
5
312C.4500
108C.1300
53.120
1.905
6
336C.2200
108C.1300
52.500
1.650
7
354C.7900
108C.1300
42.620
1.880
Nella esecuzione di un rilevo celerimetrico è spesso
necessario utilizzare due o più stazioni per rilevare
particolari non visibili dalla prima stazione.
Le operazioni di campagna che permettono di risolvere
IL RILIEVO CON DUE
questo problema prendono il nome di
O PIU’ STAZIONI
COLLEGAMENTO TRA
STAZIONI
COLLEGAMENTO TRA STAZIONI
Collegare tra loro due stazioni celerimetriche significa:
dare alla seconda lo stesso orientamento della prima
determinare le coordinate della seconda stazione
partendo dalla prima
Y
Il collegamento può essere DIRETTO se le stazioni sono tra
loro visibili o INDIRETTO se le due stazioni non si vedono
C
Y’
(AB)
COLLEGAMENTO TRA
STAZIONI
XA
A
AB
B
YA
X
Sia A la stazione iniziale e B la stazione da cui continuare il rilievo.
Dopo aver misurato i numeri generatori e calcolate le coordinate di B
si porta lo strumento in B. Al fine di orientare il cerchio nello stesso
modo della stazione A, guardando da B verso A si impone al cerchio
orizzontale la lettura
0C
(BA) = (AB) ± 200c
COLLEGAMENTO TRA
STAZIONI
DIRETTO
B
0C
(AB)
A
AB
XB= XA + AB x sen (AB)
YB = YA + AB x cos (AB)
In questo modo le letture degli angoli orizzontali, effettuate
dalla stazione B verso i punti ad essa collegati, saranno
utilizzate per il calcolo delle coordinate totali dei punti rilevati
Y
X1
X1(B) = B1 X sen (B1)
1
COLLEGAMENTO TRA
STAZIONI
Y1(B) = B1 X cos (B1)
DIRETTO
XB
(B1)
B1
B
(AB)
XA
A
X1 = XB + B1 x sen (B1)
Y1 = YB + B1 x cos (B1)
X
Y
XA
YA
QA
X1 = XA + A1 x sen (A1)
Y1 = YA + A1 x cos (A1)
Q1 = QA + ∆A1
X2 = XA + A2 x sen (A2)
Y2 = YA + A2 x cos (A2)
Q2 = QA + ∆A2
X3 = XA + A3 x sen (A3)
Y3 = YA + A3 x cos (A3)
Q3 = QA + ∆A3
XB = XA + AB x sen (AB)
YB = YA + AB x cos (AB)
QB = QA + ∆AB
X4 = XB + B4 x sen (B4)
Y4 = YB + B4 x cos (B4)
Q4 = QB + ∆B4
1
COLLEGAMENTO TRA
2
STAZIONI
(AB)
DIRETTO
IL RILIEVO E IL
CALCOLO DELLE
COORDINATE
3
5
XA
A
6
4
AB
7
B
YA
8
X
Nel collegamento indiretto le due
stazioni A
e B non sono tra loro
visibili. Risulta quindi impossibile
misurare la distanza AB e l’azimut
M
(AB)
BM
AM
COLLEGAMENTO TRA
B
STAZIONI
Si
scelgono
quindi
due
punti
ausiliari M e N visibili dalle due
INDIRETTO
stazioni
BN
(AM)
le due distanze AM e AN e gli
(AN)
A
Facendo stazione in A si misurano
azimut (AM) e (AN); dalla stazione
AN
N
B si misurano le due distanze BM e
BN e l’angolo nel vertice B
E’ possibile subito calcolare le coordinate di M e N
XM = XA + AM x sen (AM)
YM = YA + AM x cos (AM)
(MB)
XM
XN = XA + AN x sen (AN)
YN = YA + AN x cos (AN)
M
note le coordinate è possibile il calcolo della distanza
(BM)
MN e dell’azimut (MN)
M̂
YM
MN = √ [ (XN - XM)2 + (YN – YM)2 ]
B
B̂
(MN) = tg-1 [ (XN - XM) / (YN – YM) ]
nel triangolo MNB si ottiene con il teor. dei seni
M = sen-1 (BN x sen B / MN)
COLLEGAMENTO TRA
STAZIONI
MN
e per differenza
INDIRETTO
(MB) = (MN) – M
nota la distanza MB misurata e l’azimut (MB) calcolato
(AM)
si ottengono le coordinate del punto di stazione B
passando per M
A
XB = XM + MB x sen (MB)
N
XN
YB = YM + MB x cos (MB)
l’orientamento del cerchio orizzontale in B identico a
quello nel punto A si ottiene imponendo da B verso M la
YN
lettura
(BM) = (MB) ± 200c
orientato il C.O. è possibile continuare il rilievo dalla
stazione B
Y
(MC)
M
C
(CM)
COLLEGAMENTO TRA
STAZIONI
IL RILIEVO E IL
CALCOLO DELLE
COORDINATE
9
(AM)
INDIRETTO
8
XA
10
A
YA
XA
YA
QA
XM = XA + AM x sen (AM)
YM = YA + AM x cos (AM)
QM = QA + ∆AM
XC = XM + MC x sen (MC)
YC = YM + MC x cos (MC)
QC = QM + ∆MC
X8 = XC + C8 x sen (C8)
Y8 = YC + C8 x
B cos (C8)
Q8 = QC + ∆C8
X9 = XC + C9 x sen (C9)
Y9 = YC + C9 x cos (C9)
Q9 = QC + ∆C9
X10 = XC + C10 x sen (C10)
Y10 = YC + C10 x cos (C10)
Q10 = QC + ∆C10