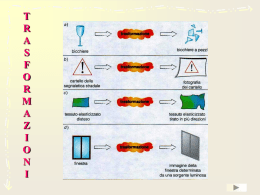
TRASFORMAZIONI GEOMETRICHE
DEFINIZIONE
AFFINITA’
TRASLAZIONI
SIMILITUDINI
ISOMETRIE
ROTAZIONI
DILATAZIONI
OMOTETIE
SIMMETRIE
USCITA
TRASFORMAZIONI
GEOMETRICHE
Una trasformazione geometrica è una
corrispondenza biunivoca tra i punti di un piano
P(x,y)  P’(x’,y’)
L’espressione analitica della trasformazione è data da
 x'  f  x 
t: 
 y'  g x 
USCITA
TRASFORMAZIONI GEOMETRICHE

IDENTITA’: trasformazione che associa ad
ogni punto il punto stesso

TRASFORMAZIONE INVOLUTORIA:
- trasformazione uguale alla sua inversa;
- applicata 2 volte, dà un’identità

AFFINITA’: Particolari trasformazioni
USCITA
AFFINITA’
 x'  a1 x  b1 y  c1
t: 
 y'  a 2 x  b2 y  c2
  a1b2  a2b1
se   0  affinità diretta AB  AB
se   0  non è un' affinità
se   0  affinità indiretta
o contraria AB  BA
USCITA
AFFINITA’

Si conservano l’allineamento tra i punti
e il parallelismo
 Si trasformano coniche in coniche
PARTICOLARI AFFINITA’
ISOMETRIE
SIMILITUDINI
DILATAZIONI
USCITA
ISOMETRIE
Si conservano le distanze tra punti
Condizione affinchè un’affinità sia un’isometria
a12 + a22 = b12 + b22 = |a1b2 – a2b1 | = 1
PARTICOLARI ISOMETRIE
SIMMETRIE
ROTAZIONI
TRASLAZIONI
USCITA
SIMMETRIE

SIMMETRIA CENTRALE rispetto ad un punto
C  xC ; y C 
 1
 x '  2 xC  x
C : 
 y'  2 yC  y


SIMMETRIA ASSIALE rispetto ad una retta
r:y=mx+q
  1
 x'  x cos 2    y  q  sen 2 
 y '  x sen 2    y  q  cos 2 
r : 
r
USCITA
ROTAZIONI
=1
Dato un punto C e un angolo orientato 
 C ,
 x'  x  xC  cos    y  yC  sen   xC
: 
 y'  x  xC  sen    y  yC  cos   yC
La trasformazione inversa di una
rotazione è sempre una rotazione di
centro C ma di angolo – 
USCITA
TRASLAZIONI
=1
Dato un vettore v (a,b)
 x'  x  a
: 
 y'  y  b
P x, y   P' x  a, y  b
v
USCITA
SIMILITUDINI
Condizione affinchè un’affinità sia una similitudine
a12 + a22 = b12 + b22 = │ a1b2 – a2b1 │ = k2 = D
dove k è il rapporto di similitudine
se k = 1
la similitudine è un’isometria
Similitudine diretta
  a 2  b2  0
x’ = ax + by + c1
y’ = - bx + ay + c2
k 2  a 2  b2
Similitudine inversa
x’ = ax + by + c1
y’ = + bx - ay + c2
   a 2  b2  0
k 2   a 2  b2
USCITA
OMOTETIE
Un’omotetia di centro O(0;0) ha equazioni:
 x'  k x
:
 y'  k y
Con
k  R  0
  k2
Le rette unite sono tutte le rette
passanti per il centro di
omotetia
USCITA
DILATAZIONI

di centro O (0,0)
 x'  h x
O : 
 y'  k y

di centro C (xc yc)
 x '  xC  h  x  xC 
C : 
 y'  yC  k  y  yC 