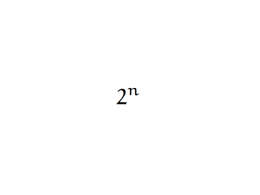Proprietà delle matrici con
variabili standardizzate
Con variabili standardizzate
Valori standard
Con media 0
Deviazione Standard = 1
Calcolo di R2y.123
Sappiamo che:
Poiché
avremo nella soluzione standardizzata:
Calcolo di R2y.123
Poiché:
si ha in generale che:
Essendo inoltre:
Sostituendo si avrà:
Calcolo di R2y.123
Sappiamo inoltre che:
Poiché
avremo che:
Calcolo di R2y.123
Calcolo di R2y.123
Se dividiamo per (n-1) possiamo verificare le seguenti
condizioni algebriche:
essendo
Allo stesso modo avremo:
essendo
Calcolo di R2y.123
Poiché R è una matrice simmetrica, è possibile derivare:
Calcolo di R2y.123
 21
1 2
1 3
2 1
 22
2 3
Sz2z1 /(n-1)
Sz22/(n-1)=1
3 1
3 2
 23
Sz3z1 /(n-1)
Sz3z2 /(n-1)
Sz21/(n-1)=1
Sz23 /(n-1)=1
Calcolo di R2y.123
Richiamando la formula di calcolo:
dove:
si avrà: