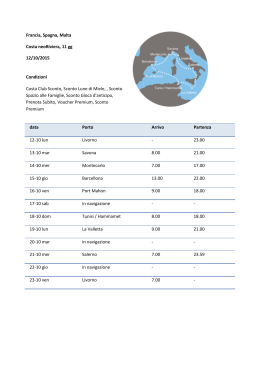
IL TEMPO E LE QUANTITA’
C (0)  C0
0
C (T )  CT
t
T
 0 istante iniziale
 T istante finale
 t istante generico
 C0 capitale iniziale (chiamato anche valore attuale);
 CT capitale finale (chiamato anche montante);
1
CAPITALIZZAZIONE
C (T )  CT
C (0)  C0
0
t
T
 CT  C0  IT premio (interesse) che viene riconosciuto
al risparmiatore per avere depositato, nel periodo 0, T , il capitale
iniziale C0 , per cui CT  C0  IT .
IT rappresenta il margine di contribuzione sul capitale iniziale;
CT  C0 IT


 i (T ) tasso di interesse nel periodo 0, T ;
C0
C0
i(1)  i indica il tasso di interesse (unitario) nell’unità di tempo
altro non è che il mark up
2
ATTUALIZZAZIONE
C (T )  CT
C (0)  C0
0
t
T
CT  C0  DT sconto che deve essere applicato al capitale finale CT
per anticiparlo
all’inizio del periodo 0, T , per cui C0  CT  DT ;
CT  C0 DT

 d (T ) tasso di sconto nel periodo 0, T ;
CT
CT
in particolare d (1)  d tasso di sconto nell’unità di tempo,
è il margine di contribuzione
percentuale
3
RELAZIONE TRA TASSO DI INTERESSE
E TASSO DI SCONTO
•
i
d
1 i
ovvero
d
i
1 d
4
LA FUNZIONE DI CAPITALIZZAZIONE
CT  f (C0 ,T )
f
0
C0
f
0
T
f (C0 ,T )  C0 f (1,T )  C0 g (T )
C0  f (C0 , 0)  C0 f (1,0)  C0 g (0)
f (1,0)  g (0)  1
5
LA FUNZIONE DI ATTUALIZZAZIONE
C0  v(CT , T )
v
0
CT
v
0
T
C0  v(CT ,T )  CT v(1,T )  CT w(T )
C0  v(C0 , 0)  C0v(1, 0)  C0w(0)
v(1,0)  w(0)  1
6