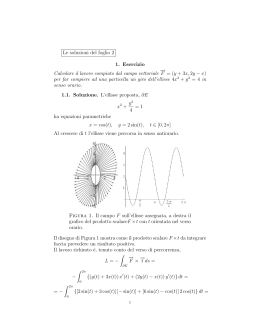
SUPERFICIE
NELLO SPAZIO,
LORO AREA.
FORMULE DELLA
DIVERGENZA
E DI STOKES
Argomenti della lezione
 Superficie nello
spazio. Loro area
 Formule della
divergenza e di Stokes
SUPERFICIE
NELLO SPAZIO.
LORO AREA
Già abbiamo incontrato le superficie
in R3 come grafico di una funzione.
Converrà presentare altri modi per
descrivere una superficie;
precisamente ci occuperemo
della loro rappresentazione
implicita come superficie di livello
di una funzione f(x,y,z) e della
loro rappresentazione parametrica
x = x(u,v)

y = y(u,v)
z z(u,v)
 =
con x(u,v), y(u,v), z(u,v) funzioni
definite sulla chiusura di un aperto
connesso E  R2, che supporremo
sufficientemente regolari:
tipicamente di classe C1(E)
Cominciamo ad occuparci delle
superficie in forma implicita. Sia
Dunque data una funzione f: A  R3  R
che supporremo sufficientemente
regolare: solitamente funzione di
classe C1(A)
Per il teorema di Dini sulle funzioni
implicite sappiamo che se f(x0,y0,z0)
= 0 e fz(x0,y0,z0) ≠ 0, allora esistono un
intorno U di (x0,y0) e uno V di z0, tali
che l’insieme dei punti che soddisfano
l’equazione f(x,y,z) = 0 e che stanno
in U  V è il grafico di una funzione
z = g(x,y), definita su U e a valori
in V, di classe C1(U)
Dunque, sotto ipotesi di sufficiente
regolarità, un’equazione f(x,y,z) = 0
è in grado di descrivere una
superficie in R3
Determiniamo l’equazione del piano
tangente a una superficie
implicitamente definita in un suo
punto (x0,y0,z0)T
Consideriamo una curva regolare che
giace sulla superficie e che passa per
il punto (x0,y0,z0)T
Tale curva abbia equazioni
parametriche x = x(t), y = y(t),
z = z(t). Deve accadere che
F(t) = f(x(t), y(t), z(t)) = 0 per ogni
t in [0,1] e, per esempio, x(0) = x0 ,
y(0) = y0 e z(0) = z0 .
Poiché necessariamente F’(t) = 0,
è, in particolare, F’(0) = 0; ma
F’(0) = <grad f(x(0),y(0),z(0)),
(x’(0),y’(0),z’(0))T > = 0
Dunque ogni vettore tangente alla
superficie e passante per (x0,y0,z0)T
è ortogonale a grad f(x0,y0,z0)
Ma i vettori ortogonale a un
assegnato vettore di R3 stanno tutti
su uno stesso piano.
Questo piano si dice il piano tangente
alla superficie in (x0,y0,z0)T
Dunque l’equazione del piano
tangente alla superficie f(x,y,z) = 0
in (x0,y0,z0)T è in termini vettoriali
0
0
0
0
0
0 T
f
(x
,
y
,
z
),(x
x
,
y
y
,
z
z

- ) =0
ossia, esplicitamente:
(∂xf)0(x-x0) + (∂yf)0(y-y0) +
(∂zf)0(z-z0) = 0
Dove (∂xf)0 indica la derivata
parziale di f rispetto a x calcolata in
(x0,y0,z0)T e notazioni analoghe per
le altre derivate parziali.
Il vettore grad f(x0,y0,z0) è normale
alla superficie f(x,y,z) = 0 nel punto
(x0,y0,z0)T
Supponiamo ora che una superficie
 sia data in forma parametrica
: E  R2  R3
con (u,v)  E e (u,v) =
( x(u,v), y(u,v), z(u,v) )T
Diremo che la superficie  è regolare
se è di classe C1(E) e inoltre la matrice
jacobiana ha caratteristica massima,
cioè 2, in ogni punto interno di E.
xu

x v

yu
yv
zu 

zv 
Esempi di questa situazione sono:
(u,v) = (R sen u cos v, R sen u sen v,
R cos u)T , E = [0, π]  [0, 2π] :
(sfera di centro l’origine e raggio R)
Una superficie si dirà semplice se
(u1,v1)T ≠ (u2,v2)T implica (u1,v1) ≠
(u2,v2) quando almeno uno dei due
punti è interno ad E
Consideriamo una superficie regolare
semplice e un punto (u0,v0)T  E. Al
variare di u in modo che (u,v0)T  E
otteniamo una linea d’equazione
(u, v0) che giace su  e passa per
(u0, v0). Analogamente troveremo
una linea d’equazione (u0, v) che
giace su  e passa per (u0, v0). Tali
linee si diranno linee coordinate della
superficie passanti per x0 = (u0, v0).
Per le ipotesi fatte sul rango della
matrice jacobiana, sappiamo che i
due vettori u(u0, v0) e v(u0, v0) sono
linearmente indipendenti e sono
tangenti alla superficie. Il vettore
u(u0, v0) v(u0, v0) è ortogonale a 
L’equazione del piano tangente si
ottiene sviluppando il determinante
x - x0
y - y0
z - z0
xu (u 0 ,v 0 ) y u (u 0 ,v 0 ) zu (u 0 ,v 0 ) = 0
xv (u 0 ,v 0 ) yv (u 0 ,v 0 ) zv (u 0 ,v 0 )
Se, in particolare, la superficie è
data in forma cartesiana, x = u,
y = v, z = f(u,v), il vettore normale
è (1,0,fu)T (0,1,fv)T =
V
N = - fu e1 - fv e2 + e3
Il vettore ha norma
|N| = √[1+|grad f|2]
Il versore normale è n = N/|N|
Vogliamo ora occuparci del problema
della definizione dell’area di una
superficie regolare. Il problema non è
banale, poiché l’idea intuitiva di
approssimare una superficie con tratti
di superficie triangolare, prendendo
il sup di queste aree, non è praticabile.
Infatti semplici esempi mostrano
come anche un cilindro possa essere
avvolto con carta sufficientemente
“increspata” in modo che il sup sia +∞
Partendo dall’osservazione che l’area
di un parallelogramma delimitato da
due vettori a e b è data dal modulo
del prodotto vettoriale di a e b,
definiremo elemento d’area sulla
superficie  come segue
ds =|  u
v |dudv
Cioè d s = |N| dudv
Data una superficie regolare semplice
 d’equazione  : E  R2  R3
definiremo area della superficie il
valore del seguente integrale
A () = E | u
|N | dudv
v | dudv = 
E
Se  è data in forma cartesiana
esplicita
2
(
)
|
f
|
A  =  1+  dxdy
E
Se  è la sfera di centro l’origine e
raggio R, avente l’equazione
parametrica già ricordata, si trova
d s = R2 sen u dudv , con 0 ≤ u ≤ π
e 0 ≤ v ≤ 2 π. L’area è
p
2p
0
0
A () = R2  senudu  dv = 4pR2
Supponiamo che sia data una linea
nel piano x z, x ≥ 0, d’equazione
(u) = (x(u),z(u))T , u  [a,b] . Se
facciamo rotare questa linea intorno
all’asse z di un angolo   ]0,2 π] ,
otteniamo una figura di rotazione.
Ricordiamo che
x=
 xds
l( )
dà l’ascissa del baricentro della curva
 . L’equazione della superficie di
rotazione è
(u,v) = (x(u) cos v,x(u) sen v,z(u))T
con E = [a,b]  [0,]
u(u0, v0) v(u0, v0) =
(- x(u)z’(u) cos v, -x(u)z’(u) sen v,
x(u) x’(u) )T
V
e il modulo è
|  u  v | = x 2 (u) + z 2 (u)x(u) =| (u)| x(u)
Ma
A () = E |(u)|x(u)dudv =   x(u)ds

Cioè
A () =   x  l( )
Quanto abbiamo appena enunciato
è il Primo teorema di Pappo-Guldino
L’area di una superficie di rotazione
ottenuta rotando di un angolo  
]0,2 π] attorno all’asse z una curva
regolare semplice  è data da
A () =   x  l( )
dove x è l’ascissa del baricentro di
(I)
L’area del toro ottenuto rotando
intorno all’asse z un cerchio di raggio
r nel piano x z , cerchio a distanza
R > r con centro sull’asse x è
A(T) = 2π R (2π r) = 4 π2 R r
-3
-2
-1
1
0.5
0
0
-0.5
1
-1
-3
-2
2
-1
0
1
2
3
3
z
+
r
R
x
z
E
x
Sia E un dominio del piano x, z , con
x ≥ 0, e lo si faccia rotare di un
angolo   ]0,2 π] , intorno all’asse z.
Vogliamo determinare il volume del
solido di rotazione S generato da E.
Sia D = E  [0,] e sia F: D  S data
da F(u,v,w) = (u cos w, u sen w, v)T
che ha determinante jacobiano
=u>0
Allora
V (S) =  1dxdydz =  u dudvdw =
D
S

=  dwE ududv =   xdm
E
0
=   x  m(E)
dove x è l’ascissa del baricentro
del dominio E . Dunque abbiamo
Secondo teorema di Pappo - Guldino
Il volume di un solido di rotazione S
ottenuto rotando di un angolo
  ]0,2 π] , intorno all’asse z un
dominio E, contenuto nel piano x, z,
con x ≥ 0 è dato da
V(S) =  x m(E)
dove x è l’ascissa del baricentro
geometrico di E.
Applicato al toro, questo teorema
ci dà il volume
V(T) = 2πR π r2 = 2π2 R r2
FORMULE DELLA
DIVERGENZA
E DI STOKES
Una superficie regolare  si può
orientare localmente scegliendo
come positivo uno dei due
orientamenti possibili del
vettore normale N o -N. In
generale si potrà dire che è data,
almeno localmente, un’orientazione
positiva se in un intorno di uno
stesso punto è assegnata
un’orientazione dell vettore
normale.
Il vettore normale, se la superficie
è regolare, varia in modo continuo
con il punto nel quale è calcolato.
Se, al variare del punto sulla
superficie n è una funzione continua
su tutta la superficie, allora la
superficie  si dice orientabile.
Sfortunatamente esistono superficie
non orientabili quali il
nastro di Möbius
1
0.5
0
-0.5
2
1
-1
0
-2
-1
-1
0
1
-2
2
3
Il nastro di Möbius ha equazioni
1
x(u , v) = ( r + hu  cos( v)) cos(v)
2
1
y (u , v ) = ( r + hu  cos( v)) sen(v)
2
1
z (u , v) = hu  sen( v)
2
con 0 ≤ v ≤ 2π e -1 ≤ u ≤ 1, r > h
Ma molte superficie sono orientabili
come la sfera o come le superficie
che delimitano un dominio normale
rispetto al piano x y.
Data una funzione f : A  R3  R ,
f continua, e data una superficie
regolare con sostegno  = (E)  A ,
definiremo l’integrale superficiale di
f esteso a , come segue
 fds = E f ( (u,v))|  u  v | dudv

Se indichiamo con E = | u|2 , con
G = | v|2, e con F = < u, v> si
trova che
| u
v |= E  G - F
2
Sia dato un dominio regolare D
normale rispetto al piano x y,
delimitato da due superficie di classe
C1(A), ,  : A  R2  R e sia Z(x,y,z)
una funzione continua con la sua
derivata rispetto a z su un aperto 
contente D.
Allora vale il seguente
Teorema
(Formula di Gauss)
Nelle ipotesi dette in precedenza, si ha
 Zz (x, y, z)dxdydz =  Z ne ,e3 ds
+s
D
Qui si è scelta come positiva la
normale esterna. Dalla formula di
riduzione per corde si ha
 (x,y)
 Zz dxdydz =  dxdy(  Zz dz)
D
A
 (x,y)
=  Z(x, y,  (x, y))dxdy -  Z(x, y,  )dxdy
A
A
Z
n
,
e
d



s
e
= +s
3
Più in generale, con procedimenti
analoghi, si può dimostrare che
T
(X
Y
Z
)dxdydz
(X,Y
,
Z)
, ne ds

x +
y +
z
=  
D
s
Lo scalare Xx + Yy + Zz si dice la
divergenza del campo F = (X,Y,Z)T :
div F
Dunque la divergenza di un campo
su un dominio D uguaglia il flusso
uscente dalla superficie laterale
Infine abbiamo il teorema di Stokes
Teorema
(Teorema di Stokes)
Sia A un dominio nel piano x y avente
frontiera A gen. reg. e orientata
positivamente. Sia f(x,y) di classe C1(A)
Sia X(x,y,z) continua con le derivate
Xy e Xz su un aperto contenente f(A).
Allora vale
 Xdx = 
G
(- X y  n, e3  + X z  n, e2  ) ds

dove G = f(A)
Infatti, posto g(x,y) = X(x,y f(x,y)),
risulta gy = Xy + Xz fy
Per Green
 Xdx =  gdx = -
A
G
g y dxdy =
A
-  ( X y + X z f y )dxdy =
A
=  ( - X y  n, e3  + X z  n, e2  )ds
s
Se Y(x,y,z) e Z(x,y,z) soddisfano
ipotesi analoghe con le loro derivate
opportune, e la superficie è
rappresentabile esplicitamente anche
nelle variabili x, z e y, z, allora
 ( Xdx + Ydy + Zdz ) =
G
con F = (X,Y,Z)T
s
rotF , n ds
n
G
s
A
A