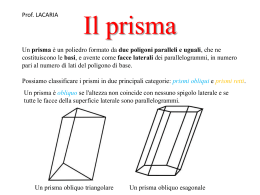
Formule generali per il calcolo di
superficie e volume di solidi a 2
basi
by iprof
RIASSUMIAMO CON IL DIAGRAMMA AD ALBERO
SOLIDI GEOMETRICI a 2 basi
POLIEDRI
Solidi di rotazione
PRISMI
cilindri
PARALLELEPIPEDI
CUBO
I prismi retti
Un prisma si dice retto se i suoi spigoli laterali sono
perpendicolari ai piani delle basi.
Un prisma si dice regolare se è retto
e ha per basi due poligoni regolari.
QUADRATO
TRIANGOLO
EQUILATERO
ESAGONO
REGOLARE
Apriamo… un prisma
Consideriamo il modello in cartone di
un prisma retto a base triangolare.
Se lo tagliamo lungo i suoi spigoli in
modo da poterlo distendere su un piano,
otteniamo una figura piana che si chiama
sviluppo della superficie del prisma.
La superficie di tutte le facce
di un solido è detta
superficie totale, mentre
quella delle sole facce laterali
è detta superficie laterale.
Alcuni esempi
Il solido P è un prisma quadrangolare
regolare, quindi è retto, le facce laterali
sono 4 rettangoli R congruenti e le
sue basi sono due quadrati Q congruenti.
P
Qui sotto è disegnato lo sviluppo della
superficie del solido P.
parallelepipedo
LA PARABOLA E LA SUA EQUAZIONE
/1
5
4. CALCOLO DELLE AREE
DEFINIZIONE
Superficie di un poliedro
La superficie di un poliedro è la somma delle superfici di tutte le sue facce.
Scomponendo un solido (anche non poliedrico) è possibile calcolarne la superficie laterale:
Al = Pb . h
Ricordiamo che alla superficie laterale va
aggiunta la superficie delle basi per calcolare
l’area totale.
Copyright © 2011 Zanichelli editore
Bergamini, Trifone, Barozzi – La matematica del triennio
At= 2Ab + Al
LA PARABOLA E LA SUA EQUAZIONE
/1
5
•cubo
l
Area di base
Ab=l2
Area laterale
Ab= 4 l2
Area totale
Copyright © 2011 Zanichelli editore
At= 6 l2
Bergamini, Trifone, Barozzi – La matematica del triennio
SOLIDI DI ROTAZIONE
SI OTTENGONO FACENDO RUOTARE UN
POLIGONO, PER 3600, INTORNO AD UN SUO
LATO
UN RETTANGOLO RUOTA INTORNO AD UNA
DIMENSIONE
CILINDRO RETTO
ASSE DI ROTAZIONE
RAGGIO DI BASE
È sempre possibile ottenere lo sviluppo della superficie
di un cilindro
CILINDRO
RETTO
poliedri a due basi
Ab
Al = Pb x h
Al
cilindro
Al = C x h
Ab
Pb
Circonferenza C=2πr
C
At = Al + 2Ab
Area
cerchio
Area cerchio Ab= πr2
Superficie del cilindro
LA PARABOLA E LA SUA EQUAZIONE
5. CALCOLO DEI VOLUMI
/1
per tutti i solidi a due basi V=Ab x h (nel cilindro Ab=πr2) 5
TEOREMA
TEOREMA
TEOREMA
Volume del cubo
Volume del prisma
Volume del cilindro
La misura del volume del La misura del volume del
La misura del volume del
Vediamo
che,
in
generale,
il
volume
delle
tre
figure
può
essere
espresso
come prodotto
cubo è uguale alla misura del prisma è uguale al prodotto
cilindro
è uguale
ap prodotto
tra
superficie
l’altezza.
suo l’area
spigolodella
elevato
alla terzadi base
dellaemisura
dell’area di base
dell’area del cerchio di base per
potenza:
per la misura dell’altezza:
la misura dell’altezza:
V = a3 o meglio V = l3
V = Ab . h
Perché V= l2 x l
Cioè V=Ab . h
Copyright © 2011 Zanichelli editore
Bergamini, Trifone, Barozzi – La matematica del triennio
V =π .r2 . h che significa
sempre V=Ab . h
Riepilogando…aree di solidi a due basi
Area di
base
Prismi
Dipende dal
poligono di
base
Parallelepipedi
Ab=bh (rettangolo)
Cubi
Ab=l2
Ab=l2 (quadrato)
Area
laterale
h=
Al
Pb
Al= Pbh
Al
Pb=
Cilindri
Ab=πr2
r
Ab=4l2
h
At=2Ab+Al

C=2πr
C=πd
r
Area
totale
Ab
C
2
oppure
d
C

Riepilogando…..volume di solidi a due basi
• V=Abh
V
Ab 
h
..
V
h
Ab
…….e peso di qualunque tipo di solido
*
*
P=V ps
P
V
ps
P
ps 
V
Il peso specifico di una sostanza è noto. Esiste la tabella dei pesi specifici. Il suo
valore indica di quanto vale il rapporto tra il peso di un cubetto di volume unitario di
una sostanza rispetto al peso di un uguale cubetto di acqua, che ha ps=1 (1 cm2
pesa 1 g)