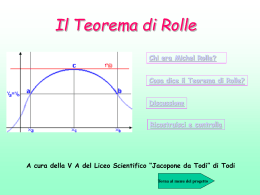
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Michel Rolle
(1652-1718)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
tangente
curva
Punto a tangente
orizzontale
a
b
Una curva regolare
(ovvero senza salti o
spigoli) che unisce
due punti di uguale
ordinata deve avere
per forza un punto
a tangente
orizzontale
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Per rendere questo
un teorema
matematico è
necessario
formularlo in modo
rigoroso e poi
dimostrarlo
tangente
curva
Punto a tangente
orizzontale
a
b
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
•
•
•
•
Senza salti = funzione continua
Senza spigoli = funzione derivabile
Punti a uguale ordinata: f(a)=f(b)
Punto a tangente orizzontale: f’(c)=0
TEOREMI CLASSICI
DELL’ANALISI
Quindi:
TEOREMA DI ROLLE
Sia f definita su un intervallo chiuso [a,b]
• continua su tale intervallo
• derivabile salvo al più agli estremi
• e sia f(a)=f(b)
Allora esiste un punto c interno
all’intervallo [a,b] tale che f’(c)=0
TEOREMI CLASSICI
DELL’ANALISI
Dimostrazione
TEOREMA DI ROLLE
CASO 1: sia f una funzione costante
In tal caso il teorema è banale perché
una funzione costante ha derivata
ovunque uguale a zero, quindi c è un
punto qualsiasi dell’intervallo
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Caso f costante
curva
tangente
Punti a tangente
orizzontale:
TUTTI!
a
b
TEOREMI CLASSICI
DELL’ANALISI
Dimostrazione
TEOREMA DI ROLLE
CASO 2: sia f non costante
Poiché la funzione è continua su un
intervallo chiuso, per il teorema di
Weierstrass essa ammette un massimo
assoluto, M, e un minimo assoluto, m.
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Poiché la funzione non è costante
massimo e minimo sono diversi (M≠m),
il che significa che massimo e minimo
non possono cadere entrambi agli
estremi dell’intervallo [a,b], altrimenti
sarebbero uguali: infatti f(a)=f(b)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Caso f non
costante; qui
per esempio il
massimo cade
all’interno
dell’intervallo
M
curva
F(a)=F(b)
a
b
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Supponiamo che sia M a cadere
all’interno dell’intervallo e che c sia la
sua ascissa
f(c)=M
In tal caso c, oltre a essere punto di
massimo assoluto, è anche punto di
massimo relativo
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Ma il teorema di Fermat dice che nei
punti di massimo relativo la derivata è
uguale a zero, quindi
f’(c)=0
CVD
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Il teorema di Rolle fornisce una
condizione sufficiente ma non
necessaria per avere un punto
stazionario: una funzione può avere un
punto stazionario anche senza
soddisfarne le ipotesi
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Queste funzioni non soddisfano una
delle ipotesi del teorema (quale…?) e
non hanno punti stazionari
• y=fraz(x)
• y=|x|
• y=x
[0,1]
[-1,1]
[0,1]
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Queste funzioni non soddisfano una
delle ipotesi del teorema (quale…?) e
hanno punti stazionari
• y=D(x)
• y=|x2-1|
• y=x2
[0,1]
[-2,2]
[-1,2]
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI ROLLE
Questa non è derivabile agli estremi,
ma questa ipotesi non è richiesta e
quindi la funzione cade sotto il dominio
del teorema di Rolle
Y=√(1-x2)
[-1,1]
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Augustin Louis
Cauchy
(1789-1857)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Siano f e g definite su un intervallo
chiuso [a,b]
• continue su tale intervallo
• derivabili salvo al più agli estremi
• e sia g(a)≠g(b), g’(x)≠0
Allora esiste un punto c interno
all’intervallo [a,b] tale che:
f (b)  f (a) f ' (c)

g (b)  g (a) g ' (c)
TEOREMI CLASSICI
DELL’ANALISI
Dimostrazione
TEOREMA DI CAUCHY
Consideriamo la funzione ausiliaria F(x)
così definita:
F ( x)  f ( x)  K  g ( x)
Dove K è una costante presa in modo che
F soddisfi tutte le ipotesi del teorema di
Rolle
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Poiché f e g sono continue e derivabili
anche F lo è, quindi basta fare in modo
che sia:
F(a)=F(b)
Sostituendo:
f (a)  K  g (a)  f (b)  K  g (b)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Con qualche calcolo si ricava il valore di
K
f (b)  f (a)
K
g (b)  g (a)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Poiché con questo valore di K la
funzione F soddisfa le ipotesi del
teorema di Rolle, allora esiste un punto
c interno all’intervallo in cui risulta:
F’(c)=0
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Ma poiché F è:
F ( x)  f ( x)  K  g ( x)
Derivando:
F ' ( x)  f ' ( x)  K  g ' ( x)
E uguagliando a zero:
0  f ' ( x)  K  g ' ( x)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Ovvero:
f ' ( x)
K
g ' ( x)
f
(
b
)

f
(
a
)
E ricordando che K è: K 
g (b)  g (a)
Sostituendo:
CVD
f (b)  f (a) f ' (c)

g (b)  g (a) g ' (c)
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI LAGRANGE
Giuseppe Luigi
Lagrange
(1736-1813)
Il teorema è un caso
particolare di quello
di Cauchy
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI LAGRANGE
Sia f definita su un intervallo chiuso [a,b]
• continua su tale intervallo
• derivabile salvo al più agli estremi
Allora esiste un punto c interno
all’intervallo [a,b] tale che:
f (b)  f (a)
 f ' (c )
ba
TEOREMI CLASSICI
DELL’ANALISI
Dimostrazione
TEOREMA DI CAUCHY
Basta ricordare la formula di Cauchy
f (b)  f (a) f ' (c)

g (b)  g (a) g ' (c)
E prendere g(x) = x
TEOREMI CLASSICI
DELL’ANALISI
TEOREMA DI CAUCHY
Infatti se g(x)=x allora:
g (a)  a
g (b)  b
g ' (c )  1
E inserendo questi risultati nella formula:
f (b)  f (a) f ' (c)

g (b)  g (a) g ' (c)
CVD
f (b)  f (a)
 f ' (c )
ba
TEOREMI CLASSICI
DELL’ANALISI
tangente
F(b)
corda
curva
F(a)
a
c
b
Il teorema di
Lagrange ha un
evidente
significato
geometrico
TEOREMI CLASSICI
DELL’ANALISI
Infatti:
tangente
C
F(b)
B
corda
curva
F(a)
A
a
c
A(a,f(a))
b
B(b,f(b))
f (b)  f ( a )
ba
È il coefficiente
angolare della
retta AB, corda
sottesa dall’arco
di curva
TEOREMI CLASSICI
DELL’ANALISI
Mentre:
tangente
C
F(b)
B
corda
È il coefficiente
angolare della
tangente alla
curva in C
curva
F(a)
A
a
f ' (c )
c
b
TEOREMI CLASSICI
DELL’ANALISI
tangente
C
F(b)
B
corda
curva
Il teorema di
Lagrange dice
che questi
coefficienti sono
uguali
F(a)
f (b)  f (a)
 f ' (c )
ba
A
a
c
b
TEOREMI CLASSICI
DELL’ANALISI
tangente
C
F(b)
B
corda
curva
F(a)
A
a
c
b
Ma se due rette
hanno lo stesso
coefficiente
angolare allora
sono parallele
TEOREMI CLASSICI
DELL’ANALISI
tangente
C
F(b)
B
corda
curva
F(a)
A
a
c
b
Quindi: in un
arco di curva
regolare c’è
sempre un punto
in cui la tangente
è parallela alla
corda sottesa
all’arco