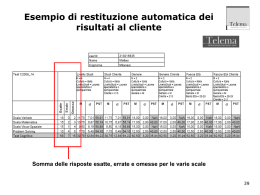
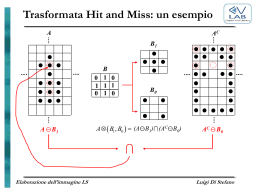
Fondamenti di Automatica
1
Lezione 2: Trasformata di Laplace
• Definizione
• Proprietà
• Antitrasformata di una funzione razionale
A.A. 2004/05
Fondamenti di Automatica
2
Trasformata di Laplace
• Strumento matematico che permette di trasformare
un’equazione differenziale lineare a coefficienti costanti nel
dominio del tempo in un’equazione algebrica.
• Riconduce il problema della soluzione di una ODE lineare a
coefficienti costanti di ordine n alla determinazione delle radici
di un polinomio di grado n.
A.A. 2004/05
Fondamenti di Automatica
3
Definizione
f (t) : R → Rr×c
L [f (t)] = F (s) =
∞
0−
f (t) e−st dt
A.A. 2004/05
Fondamenti di Automatica
4
Sommario delle proprietà
• Linearità
• Impulso di Dirac e sua trasformata
• Funzioni modali e loro trasformate
• Trasformata della derivata
• Trasformata dell’integrale
• Traslazione temporale
• Convoluzione
• Teorema del valore iniziale
• Teorema del valore finale
A.A. 2004/05
Fondamenti di Automatica
5
Linearità
L [M f (t) + N g(t)] = M F (s) + N G(s)
A.A. 2004/05
Fondamenti di Automatica
6
Impulso di Dirac e sua trasformata
Impulso unitario (delta di Dirac):


 δ(t) = 0, ∀t = 0
ε
δ(·) :


f (t)δ(t)dt = f (0), ∀f (·) continua in t = 0 e ∀ε > 0
−ε
Trasformata di Laplace:
L [δ(t)] = 1
A.A. 2004/05
Fondamenti di Automatica
7
Funzioni modali e loro trasformate - 1
Funzioni modali:
tk eat , k = 0, 1, 2, . . .
a ∈C
I
Trasformata di Laplace:
k at k!
=
L t e
(s − a)k+1
A.A. 2004/05
Fondamenti di Automatica
8
Funzioni modali e loro trasformate - 2
L [1] =
k
L t
=
L [eat ] =
L [cos(ωt)] =
L [sin(ωt)]
=
L [eσt cos(ωt)] =
L [eσt sin(ωt)]
=
1
s
k!
sk+1
1
s−a
s
s2 + ω 2
ω
s2 + ω 2
s−σ
s2 − 2σs + σ 2 + ω 2
ω
s2 − 2σs + σ 2 + ω 2
A.A. 2004/05
Fondamenti di Automatica
9
Trasformata della derivata
L f˙(t) = sF (s) − f (0− )
L f¨(t) = s2 F (s) − f (0− )s − f˙(0− )
k
L D f (t) = sk F (s) − f (0− )sk−1 − Df (0− )sk−2 −
− · · · − Dk−2 f (0− )s − Dk−1 f (0− )
se f (0− ) = Df (0− ) = · · · = Dk−1 f (0− ) = 0
k
allora L D f (t) = sk F (s)
A.A. 2004/05
Fondamenti di Automatica
10
Trasformata dell’integrale
t
L
f (σ)dσ
0
F (s)
=
s
A.A. 2004/05
Fondamenti di Automatica
11
Ritardo temporale

 1, se t ≥ τ > 0
1(t − τ ) =
 0, se t < τ

 f (t − τ ),
Segnale ritardato: f (t − τ )1(t − τ ) =
 0,
se t ≥ τ > 0
se t < τ
Trasformata di Laplace:
L [f (t − τ ) 1(t − τ )] = e−τ s F (s)
A.A. 2004/05
Fondamenti di Automatica
12
Convoluzione
t
g ∗ f (t) =
0
t
g(σ)f (t − σ)dσ =
g(t − σ)f (σ)dσ
0
Trasformata di Laplace:
L [g ∗ f (t)] = G(s)F (s)
A.A. 2004/05
Fondamenti di Automatica
13
Teorema del valore iniziale
lim+ f (t) = lim sF (s)
t→0
s→∞
se lim sF (s) esiste ed è finito.
s→∞
A.A. 2004/05
Fondamenti di Automatica
14
Teorema del valore finale (asintotico)
lim f (t) = lim sF (s)
t→∞
s→0
se entrambi i limiti esistono e sono finiti.
A.A. 2004/05
Fondamenti di Automatica
15
Antitrasformata di Laplace - Definizione
f (t) = L−1 [F (s)] se L [f (t)] = F (s)
unica se si impone f (t) = 0 per t < 0
A.A. 2004/05
Fondamenti di Automatica
16
Antitrasformata di Laplace di una
funzione razionale propria - 1
n(s)
,
R(s) =
d(s)
∂n ≤ ∂d
Decomposizione:
R(s) =
c =
n (s) =
n (s)
c +
,
d(s)
∂n < ∂d
lim R(s)
s→∞
n(s) − cd(s)
A.A. 2004/05
Fondamenti di Automatica
17
Antitrasformata di Laplace di una
funzione razionale propria - 2
n (s)
R(s) = c +
,
d(s)
∂n ≤ ∂d
caso particolare (poli semplici)
d(s) = (s − p1 )(s − p2 ) · · · (s − pn ),
p1 = p2 = · · · =
pn
sviluppo di Heaviside (in fratti semplici):
n
Ki
R(s) = c +
s − pi
i=1
Ki
=
lim (s − pi )R(s) (residui)
s→pi
Antitrasformata: r(t) = L−1 [R(s)] = c δ(t) +
n
Ki epi t
i=1
A.A. 2004/05
Fondamenti di Automatica
18
Antitrasformata di Laplace di una
funzione razionale propria - 3
n (s)
,
R(s) = c +
d(s)
∂n ≤ ∂d
caso generale
d(s) = (s − p1 )n1 (s − p2 )n2 · · · (s − pr )nr ,
p1 = p2 = · · · =
pr
sviluppo di Heaviside:
ni
r Kij
R(s) = c +
j
(s
−
p
)
i
i=1 j=1
Kij
=
1
dni −j
ni
lim
{(s
−
p
)
R(s)}
i
n
−j
i
(ni − j)! s→pi ds
Antitrasformata:
r(t) = L−1 [R(s)] = c δ(t) +
ni
r i=1 j=1
Kij
tj−1 epi t
(j − 1)!
A.A. 2004/05
Fondamenti di Automatica
19
Poli complessi coniugati ⇒ oscillazioni
Poli complessi coniugati pi = σi + jωi , pi = σi − jωi →
Residui complessi coniugati Kij , K ij
|Kij | j−1 σi t
Kij
K ij
t e cos(ωi t + ∠Kij ) =
+
→2
(s − pi )j
(s − pi )j
(j − 1)!
= αij tj−1 eσi t cos(ωi t) + βij tj−1 eσi t sin(ωi t)
2|Kij |cos(∠Kij )
2|Kij |sin(∠Kij )
, βij = −
αij =
(j − 1)!
(j − 1)!
A.A. 2004/05