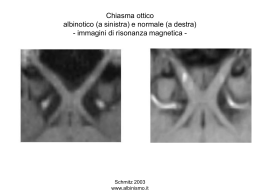
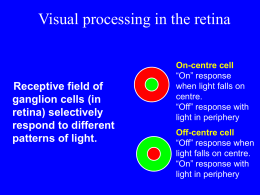
Caratteristiche ottiche del sistema visivo
Richiamiamo alcuni concetti base dei sistemi ottici. Tralasciando aspetti come la dirazione e
quanto legato alla natura ondulatoria della luce deniamo invece:
Formazione delle immagini.
Diottro semplice.
Sistemi ottici centrati.
Diaframmi.
1
Formazione dell'immagine in un sistema ottico
Un sistema ottico e una successione di superci che sono rifrangenti oppure riettenti. Le superci
sono sferiche, cilindriche e paraboliche. In particolare ci occuperemo di sistemi ottici centrati in
cui sono presenti superci sferiche con il centro su una stessa retta detto asse ottico.
2
Stigmatismo di un sistema ottico
Figura 1: Esempio generico di un sistema ottico
Con riferimento a un sistema ottico (vedi g: 1) ci poniamo il problema piu specico della
formazione delle immagini, in particolare dello stigmatismo. Con tale termine indichiamo il fatto
che punti luminosi hanno immagini puntuali, in termini pratici si ha una corretta formazione delle
immagini. Data una supercie d'onda i raggi di luce sono perpendicolari alla stessa. Consideriamo
una supercie d'onda sferica originata in A : questa onda ad un certo punto incontra diverse
superci rifrangenti del sistema ottico. Se in uscita dallo stesso la supercie d'onda 0 e ancora
sferica, i raggi paiono provenire dal punto luminoso A' immagine del punto luminoso A. Se 0e
sferica come lo era , il sistema ottico e stigmatico rispetto al punto A (diversamente e astigmatico).
I suddetti punti A (nello spazio oggetti) e A' (nello spazio immagini) sono detti coniugati. Il
sistema e generalmente stigmatico se la relazione di stigmatismo AA' vale per ogni punto dello
spazio oggetti. Cio ha rilevanza nella costruzione dell'immagine con una tecnica graca: il fatto
che il sistema ottico sia stigmatico fa si che tutti i raggi che escono da una sorgente luminosa
puntiforme devono convergere in un punto immagine. Tale punto immagine puo essere sia reale
sia virtuale (vedi g: 2).
1
Figura 2: Immagine virtuale di un oggetto reale
3
Ortoscopia
Nel sistema ottico esiste una relazione tra i raggi in uscita e quelli in entrata. Introduciamo nello
spazio immagine e nello spazio oggetti due sistemi di riferimento su assi cartesiani distinti (vedi
Figura 3: Sistema di assi di riferimento per la descrizione di un sistema ottico
g: 3). In un sistema ortoscopico i punti dei piani perpendicolari all'asse ottico hanno immagini
che stanno su piani perpendicolari nello spazio immagini (vedi g: 4). Si denisce ingrandimento
Figura 4: Esempi di piani perpendicolari all'asse ottico
angolare il rapporto
0
= !!
Questo rapporto e costante al variare di A nel piano perpendicolare all'asse. L'esistenza di questa
proprieta mi dice che il sistema e ortoscopico. Considerati un punto A e un punto B avremo
un'immagine A'B' che permette di denire l'ingrandimento lineare
G!
Gl
0 0
B
= AAB
Occorre sempre vericare se un sistema ottico soddisfa questi requisiti.
2
4
Il diottro semplice
Iniziamo un'analisi di sistemi ottici a partire dai diottri semplici per giungere ai sistemi ottici piu
complessi. Il diottro sferico e rappresentato da due mezzi, con diversi indici di rifrazione, separati
da una supercie di interfaccia sferica (vedi g: 5). Vogliamo dimostrare che sorgenti puntiformi
Figura 5: Sezione di un diottro semplice
hanno un'immagine puntiforme (stigmatismo). Generalmente un diottro non e stigmatico ma
sotto alcune ipotesi s. Considero due raggi luminosi che nascono da un punto oggetto e che vanno
a formare un'immagine puntiforme: il primo e perpendicolare all'interfaccia e prosegue inalterato,
il secondo no e viene rifratto secondo la legge
sin i1 = n2 :
sin i2 n1
Applichiamo il principio del tautocronismo: due raggi luminosi originati da una stessa sorgente
puntiforme impiegano lo stesso tempo a raggiungere una destinazione comune qualunque sia il
tragitto percorso. Uguagliando questi due tempi di percorrenza ricaviamo:
AO
c
n1
0
n2
e da questa ricaviamo n1 AO + n2 OA0 =
di = OA`) e riscriviamo
n1 d0
0
BA
+ OA
= AB
c
c + c
n1
n1 AB
n2
+ n2 BA0 . Cambiando notazione (do =
p
+ n2 di = n1 (d0 + x)2 y2 + n2
p
y2
+ (di
AO
e
)
x 2:
Si sfrutta al relazione geometrica dell'interfaccia sferica
(x
R
)2 + y2 = R2 !
x2
+ y2 = 2Rx
per riformulare la relazione precedente
n1 d0
+ n2 di = n1 d0
s
s
1 + 2d0 + 2Rx + n
d20
2 di
1 + Rx d2 xdi :
i
Solo ora interviene l'ipotesi di parassialita nella forma x R che mi permette di approssimare
p
1 + 2w = 1w. Il secondo membro va riscritto
= n1 d0 (1 + d0 xd+2 Rx ) + n2 di (1 + xR d2 xdi )
0
i
3
Globalmente tutta la nostra equazione si riduce a
0 = n1 (1 + dR ) + n2 ( 1 + dR )
0
i
Esplicitiamo la relazione che ci interessa in relazione al piano oggetti (p1 ; y) e al piano immagini
(p2 ; y0 ):
n2
n1
=
1 + pR1
1 + pR2
=)
n2
+ np2 R = n1 + np1 R =)
2
n2
1
R
n1
= np 1 + np 2
1
2
Introduciamo i fuochi, grandezze che riassumono la geometria e la sica del sistema ottico
f2
= p2 jp2 =1 = n
2
n2
f1
n1
R
= p1 jp1 =1 = n
Si puo scrivere la relazione, detta di Huygens, per il diottro semplice
f1
2
n1
n1
R
+ pf2 = 1
p1
2
che e una relazione iperbolica tra p1 e p2 . erchiamo una relazione per le y: dall'ingrandimento
lineare osserviamo che
A0 B 0
CA0
=
= pp2 + Rr = Gl = yy2
AB
CA
1
1
Possiamo determinare completamente l'immagine considerando le due
Figura 6: Relazione fra le coordinate dello spazio oggetti e dello spazio immagini
relazioni (vedi g: 6)
(
+ pf22 = 1
= pp12 +RR
Concludiamo questa esposizione con due nuove espressioni per gli ingrandimenti
Gy
f1
p1
y2
y1
= yy2 = p
1
G!
0
1
f1
f1
= !! = pp1
2
0 SR 0
se valgono tan ! = SR
p1 = ! e tan ! = p2 = ! . Per ultimo notiamo
Gy
i2
P2 n1
= yy2 = pp2 sin
sin i = p n
1
1
1
1 2
4
=)
Gy G!
= nn1
2
5
Sistema ottico centrato
Consideriamo un sistema ottico costituito da una successione di mezzi rifrattivi delimitati da
superci sferiche, i cui centri sono su una stessa retta (vedi g: 7). Sfruttiamo la simmetria
Figura 7: Esempio di un sistema ottico centrato
del sistema e diamo una caratterizzazione di tipo operativa come successione di diottri semplici.
Itero la formula del diottro semplice con opportuni cambi di riferimenti. Il sistema e ortoscopico.
Consideriamo un raggio parallelo all'asse entrante nel sistema ottico: avro nello spazio immagini
un raggio rifratto che non sara piu parallelo bensi incidera sull'asse ottico in un punto chiamato
fuoco del sistema ottico. Viceversa un raggio in uscita parallelo all'asse ottico sara originato da
un raggio entrante obliquo passante per il primo fuoco. Consideriamo i due punti Q e Q', che sono
coniugati: le loro proiezioni sull'asse ottico, O e O', sono anch'esse punti coniugati, e vengono
denite punti principali del sistema ottico. Scegliendo i punti principali come origini per lo spazio
delle immagini e lo spazio degli oggetti, il sistema ottico e descritto dalle stesse relazioni che si
hanno per il diottro semplice. La conoscenza di f f " e di O O' caratterizza completamente il
sistema ottico. Dato un punto B, sorgente puntiforme nello spazio degli oggetti, per determinare
l'immagine considero un raggio parallelo all'asse e uno passante per il fuoco. Sfrutto le proprieta
di ortoscopia e posso risalire a p0 (vedi g: 8). La dierenza rispetto al diottro semplice sta
Figura 8: Determinazione dell'immagine di un a sorgente puntiforme B
unicamente nella distanza OO', le relazioni per il resto sono identiche. Vale
0
f
+ fp0 = 1
p
cos come
Gy
0
= yy = p f f
Sono le stesse leggi che ci consentono di determinare p0 e y0 . Puo valere la pene di notare che la
relazione per il diottro semplice
f1
= nn1
f
2
2
5
iterata piu volte produce
f
f0
= nn0
in cui nulla impedisce che i due dielettrici siano identici. In questo caso la quantita 1=f e detta
convergenza ed e misurata in diottrie.
6
Diaframmi
Tutto cio che limita la dimensione trasversale di un sistema ottico e un diaframma (vedi g: 9).
Figura 9: Vari diaframmi presenti in un sistema ottico
Questo e sempre implicito in un sistema ottico data la presenza di lenti. Valutiamo il ruolo di
un diaframma in un sistema ottico. Cerchiamo di determinare tra i raggi uscenti da A quelli che
attraversano il sistema. I diaframmi, che concettualmente possono essere ovunque, vengono tutti
riportati nello spazio oggetti. Alcuni dovranno essere trasformati applicando la legge del sistema
ottico per la zona tra il diaframma e lo spazio oggetti. Dopo tale trasporto il diaframma piu
stretto che caratterizza il sistema e detto iride. Il foro dell'iride e detto pupilla e il suo centro e
il centro della prospettiva. Dato un punto A nello spazio oggetti e un diaframma fra A e l'iride,
tale diaframma e il diaframma del campo oggetti. Per evitare perdita di intensita luminosa nei
bordi delle immagini bisognerebbe che la nestra del campo oggetti coincidesse con il piano degli
oggetti luminosi.
7
Energia, luminanza e illuminamento
In un discorso di tipo energetico possiamo seguire un raronto fra grandezze di tipo radiometrico
e di tipo fotometrico. Possiamo esprimere le seguenti corrispondenze:
Energia raggiante (joule)
! Quantita di luce (lumenx)
Flusso raggiante (watt)
! Flusso luminoso (lumen)
watt
) ! Intensita luminosa (candela)
Intensita energetica ( steradianti
watt
Radianza ( steradianti
! Luminanza
(candela=m2)
m22)
Irradiamento (watt=m )
! Illuminamento
(lux=lumen=m2 )
In ambito fotometrico la grandezza fondamentale e la candela. Si stabilisce un rapporto tra
grandezze fotometriche e radiometriche attraverso un parametro detto eÆcienza luminosa.
f = r
6
La candela e stata ssata da una convenzione nel 1979 che la quantica come l'intensita pari a
quella di una sorgente monocromatica alla frequenza di 540 1012 Hz e cioe 1/683 watt/steradiante.
Discutiamo la relazione tra usso luminoso e luminanza: vale
(a)
(b)
Figura 10: (a) Porzione di immagine con relativo angolo solido e (b) Sistema ottico centrato: A'B'
e l'immagine di AB
= L d! dS
Data la luminanza dell'oggetto, vogliamo caratterizzare la luminanza dell'immagine (vedi g: 10).
In termini niti la relazione diviene
d = L S
dove / !2 S / y2 con y dimensione trasversale dell'oggetto. Si puo formulare il usso
luminoso dell'immagine come
0 = L0 0 s0
e analogamente 0 / !02 S 0 / y02 . Introducendo il fattore di trasparenza(T ) del sistema ottico
otteniamo
0 = T dove T = 1. Possiamo scrivere che la luminanza dell'immagine e pari a
!
y
L0 = L T ( 0 )2 ( 0 )2
!
y
d
sfruttando l'ingrandimento lineare nella forma
Gl
cos come G! otteniamo
0
= pp nn0
0
L0
= T ( nn )2 L
quindi se n0 = n interviene solo il fattore T per determinare L. Chiunque si aspetterebbe che
ingrandendo l'immagine questa diventi piu tenue, ma L e una grandezza specica e guardando
sotto uno stesso angolo raccolgo la stessa energia. Dato che !0 e piu piccolo l'immagine esce sotto
un angolo piu stretto.
f lusso luminoso su una superf icie
Illuminamento =
superf icie
7
S
Questo discorso non puo essere trascurato quando l'immagine viene raccolta su un sensore. Per il
usso e stato detto = LS . La vale
sezione pupilla in ingresso
=4 h2
=
= distanza
della sorgente al quadrato
p2
da cui otteniamo
2
= h
4p2 S L
Alla n ne ricaviamo l'illuminamento come
0 h2 S L
E0 = 0 =
S
4p2 S
E0
0
2
n 2
= h
4p2 ( n ) L
e qui, per oggetti lontani p f , ricaviamo
E
L
0
= (=4) ( fh )2 ( nn )2
Come considerazione nale vogliamo osservare che la quantita h=f e detta apertura numerica del
sistema ottico, o f number. Tanto e maggiore f =h tanto piu e luminosa l'immagine e minore
l'esposizione della pellicola.
8
Funzione di trasferimento ottica
Introduciamo alcuni concetti che permettono di caratterizzare come gli strumenti ottici trasformano le immagini. Cio ci permette di valutare le qualita delle immagini di uno strumento ottico(occhio, telecamere,etc..). Abbiamo gia parlato di ottica geometrica per quanto riguarda gli
oggetti e le immagini e abbiamo introdotto G. Qui invece vogliamo descrivere come una sorgente luminosa e trasformata in un'immagine, con una relazione tra la distribuzione di intensita
luminosa dell'immagine e quella dell'oggetto. Per fare questo dato che le relazioni di elettromagnetismo sono lineari (come per l'occhio) i concetti che intervengono sono a noi noti. La funzione
di trasferimento e legata alla risposta impulsiva, quali sono gli aspetti delle speciche legate alle
caratteristiche siche dello strumento? Data la funzione di trasferimento ottica possiamo riassumere le varie relazioni nella gura 11. La nostra attenzione e sulla funzione di trasferimento, poi
Figura 11: Schema a blocchi delle relazioni tra diverse grandezze collegabili alla fz. di trasferimento
ottica
a ritroso torneremo a discutere gli altri punti. Supponiamo per semplicita di trattare immagini
8
monodimensionali. Vogliamo descrivere la distribuzione di intensita luminosa nello spazio oggetti
dell'oggetto Iogg (x). Ipotizziamo che questa sia una funzione Iogg (x) = 1+ a cos20 x. Deniamo
il contrasto come visibilita
Imax Imin
V
Imax + Imin
da cui V0 = a.
Introduciamo la grandezza S (x x0 ) = risposta impulsiva dello strumento ottico. Possiamo
dire che per l'immagine vale
Z
( )=
Iimm x
Iogg x0 S x
x0 dx
( ) (
)
sostituendo la relazione per Iogg otteniamo
Iimm
Z
x0 dx0
= (1 + a cos 20 a)S (x
)
Alternativamente, la Iimm e esprimibile attraverso la trasformata di Fourier inversa, grazie al
teorema della convoluzione.
Z
( ) = ( |{z}
~ )S~()e
Iimm x
= fÆ() + a2 [Æ(
0
) + Æ( + mu0 )]gS~()e
( ) = S~(0) + a2 [S~(0 )ei20 + S~(
Iimm x
Qui possiamo osservare che
~() =
S
Z
d
trasf ormata
Z
ovvero
i20 x
()
S x e
i2x
dx
S
S~ =
2 Re
Z
i20 x
0 e i20
)
d
]
S x e i2x dx
()
che ci permette di scrivere la relazione come
~(0) + a 2RefS~(0 )ei20 xg
Iimm = S
2
= S~(0) + a j S~(0 ) j cos[20 x + (0 )]
= S~( )
(1)
(2)
dove e da intendersi S~ =j S () j ei() quindi per completezza
~(0)[1 + a j S~(0 ) j cos[20 x + (0 )]]
Iimm = S
~(0)
S
Abbiamo concluso che ci sono delle modiche nella fase e nella ampiezza ma nulla cambia nella
0 )
mentre il modulo della
frequenza. Ricaviamo pertanto Vi =contrasto nell'immagine= a S~S~((0)
funzione di trasferimento ottica, detta anche MTF,
~
j (0 ) j= VVi j S~(0 ) j
S (0)
o
Piu in particolare andamenti tipici di funzione di trasferimento ottica, ad esempio per l'occhio,
sono rappresentabili come in gura 12. La composizione luminosa della sorgente viene modicata
nell'immagine che non conserva la distribuzione di contrasto, attenua meno le basse frequenze.
Cio e legato alle caratteristiche siche dell'oggetto: per la pupilla abbiamo
9
(a)
(b)
Figura 12: (a) Esempio d modulation transfer function (MTF) e (b) andamento di MTF nell'occhio
con inversione di fase in mancanza di messa a fuoco
Diametro pupilla
max (cicli/grado)
0,5
15,6
1
31,3
1,5
48
2
62,6
Talvolta quando si guarda alla f:t:o: si possono osservare anche dei valori negativi (vedi g: 12)
Procediamo a ritroso ed evidenziamo la relazione della risposta impulsiva con la distribuzione
di campo elettromagnetico. Si considerano strumenti ottici operanti in luce non coerente (illuminazione normale) per cui non c' e interferenza tra gli eetti sull'immagine di sorgenti distinte
spazialmente, c'e soltanto la somma dell'intensita. Per quel che riguarda la sorgente la esprimiamo
come una distribuzione di sorgenti puntiformi con una intensita variabile
Z
Iogg (x0 ) =
L'immagine e il risultato della somma
Iimm
=
( ")Æ(x0
f x
") "
x dx
X
(sorgenti puntif ormi)
Dunque se una distribuzione di intensita impulsiva della sorgente Æ(x0 ) riconduce a S (x x0 )
di intensita di immagine, dalla sovrapposizione degli eetti ricaviamo Iimm =
Rdistribuzione
f (x0 )S (x
x0 )dx0 . Si manifesta l'indipendenza dalle traslazioni con l'ipotesi di linearit
ae
Figura 13: Possibili immagini S sotto l'ipotesi di linearita e stazionarieta
stazionerieta spaziale (vedi g: 13). Riassumendo possiamo dire che:
10
In luce non coerente, il S.O. e lineare e stazionario rispetto l'intensita di campo
elettromagnetico
La distribuzione di intensita di immagine e calcolata sulla base della risposta della
distribuzione di una sorgente puntiforme
L'immagine (intensita) di una sorgente puntiforme e determinabile conoscendo la funzione
di trasferimento dell'apertura o diaframma del sistema ottico.
Richiamiamo un principio di ottica elettromagnetica sulla teoria scalare dell'ottica ondulatoria:
Figura 14: Fronte d'onda come insieme di sorgenti puntiformi (Huygens)
il principio di Huygens (vedi g: 14). Esso aerma che il campo magnetico generato da un'onda
puo essere determinato supponendo che ogni porzione della stessa sia una sorgente puntiforme
di onde sferiche, ovvero si ricava dalla sovrapposizione di onde sferiche puntiformi generate dai
punti della superci investite dall'onda. Possiamo scrivere che (r) = erikr e un'onda sferica. Se
abbiamo una distribuzione di campo ( ) per le sorgenti, possiamo scrivere
(x) =
Z
ik r (x; )
( ) er(x; )
d
tenendo conto di considerare distribuzioni prossime all'asse otteniamo
Z
2 2x
1
(x) =
( )eik(z+ z z ) d
z
L'eetto di una lente introduce nelle proprieta delle onde un termine di fase
distanza focale per cui
Z
2 2x
2
1
(x) = z ( )eik(z+ z z ) e ik =f d
Qui se z = f concludiamo che
(x) =
eikf
Z
( )e
f
2 x
i f
2
e ik =2f
con
f
dxd
e l'intensita luminosa sul piano focale della lente. Questa e proporzionale alla trasformata di
Fourier della distribuzione di campo sul diaframma dello strumento ottico.
L'immagine di una sorgente oggetto puntiforme (vedi g: 15)
imm (x) =
imm (x) =
=
ZZ
ZZ
ZZ
ikr
(x0 ) e r
| {z }
ik2 eiks
2f
dxd
)
s
eccitazione dalla sorgente
ogg (x0 )A( )e
ogg (x0 ) A( )e
| {z0 }
Æ (x
(A( )e
ik2 ( 1 + 1 + 1 ) ik( x0 + x ) 0
2
z z0 f e
z z dx d
0 +x)
ik ( xz
)
11
z dxd
=C
Z
()
A e
ikx
z d
Figura 15:
E quindi per concludere
( ) =j C
S x
Z
()
A e
12
ikx
z d
j2