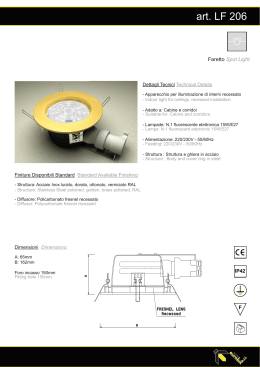
GNGTS – Atti del 23° Convegno Nazionale / 14.13
V. Lipari e G. Drufuca
Dipartimento di Elettronica e Informazione, Politecnico di Milano
MIGRAZIONE NEL DOMINIO ANGOLARE:
ZONE DI FRESNEL E FILTRAGGIO
Attraverso la migrazione di Kirchhoff effettuata nel domino negli angoli in
profondità (illustrata in dettaglio in Audebert et al., 2000, 2002, 2003) è possibile
ricavare e sfruttare utili informazioni riguardo al concetto di zona di Fresnel,
relativamente al dominio angolare.
Il dominio su cui viene effettuata la migrazione è descritto da 4 angoli
(seguendo la notazione di Audebert et al., 2000): due angoli legati all’angolo di
incidenza, chiamati angoli di scatter, che sostituiscono offset ed azimuth in
superficie, e due angoli che descrivono il vettore illuminazione (somma dei vettori di
slowness incidente e riflessa).
Gli angoli di scatter sono:
•
•
θ : Semiapertura tra i vettori di slowness
ϕ: Azimut del piano contenente i vettori di slowness
Gli angoli che descrivono il vettore illuminazione sono:
•
•
λ: Elevazione del vettore illuminazione
ψ: Azimut del vettore illuminazione.
Fissati gli angoli di scatter e il punto in profondità la migrazione alla Kirchhoff è
un integrale sulla semisfera unitaria descritta dagli angoli di illuminazione. La
migrazione nel dominio angolare permette di risolvere alcuni problemi dei classici
algoritmi di migrazione alla Kirchhoff al costo di un notevole incremento nelle risorse
di memoria richieste. Ridefinire le zone di Fresnel in questo dominio può essere utile
per una possibile ottimizzazione del binning e dell’apertura di migrazione da
utilizzare.
Si definisce la prima zona di Fresnel come la porzione di riflettore dalla quale
l’energia riflessa raggiunge il ricevitore in un tempo compreso tra il tempo di
riflessione e lo stesso aumentato della semi-durata (τ/2) dell’onda. I contributi
provenienti da questa zona interferiscono costruttivamente a formare la riflessione.
Detto Td il tempo di diffrazione e Tr il tempo di riflessione, la relazione che individua la
prima zona di Fresnel è:
(1)
Nel caso di velocità uniforme e di riflettori piani è possibile ricavare
analiticamente la relazione che determina i confini della zona di Fresnel nel dominio
angolare.
Si consideri innanzitutto il caso bidimensionale, riferendosi per semplicità al
caso zero-offset per eliminare la dipendenza dagli angoli di scatter, determinando la
dipendenza della zona di Fresnel unicamente dall’elevazione φ. L’estensione
GNGTS – Atti del 23° Convegno Nazionale / 14.13
spaziale della zona di Fresnel, sulla superficie di acquisizione, per un generico
riflettore inclinato è:
(2)
dove τ è la durata dell’ondina, v la velocità del mezzo, α è l’inclinazione del riflettore
e z la profondità del riflettore.
Le soluzioni h1,2 fornite dall’equazione rappresentano i limiti spaziali della zona
di Fresnel. Conoscendo queste e l’inclinazione α del riflettore si ottengono i limiti
della zona di Fresnel nella dimendine dell’elevazione:
(3)
A partire da questo risultato si può estendere semplicemente al caso 3D
ricavando anche la dipendenza dall’azimuth ψ.
Sempre limitandosi al caso di velocità uniforme si può calcolare analiticamente
qual’e la forma dell’impronta di un riflettore piano nel dominio angolare, in particolare
è interessante la visualizzazione di un riflettore in un CRP (z,λ) (Fig. 1).
(4)
La curva risulta avere una tangenza orizzontale in corrispondenza della
pendenza effettiva del riflettore. Facendo riferimento al CRP in Fig. 1 la migrazione
consiste nella somma lungo la dimensione delle elevazioni. I contributi che hanno la
maggior importanza nella costruzione dell’immagine migrata sono quelli vicini alla
tangenza orizzontale, ovvero quelli relativi prima zona di Fresnel. Si può quindi
studiare una strategia che permetta di sommare solo i contributi relativi a questa
zona.
Fig. 1 - Impronta di riflettori piani nel dominio angolare (pendenze del riflettore rispettivamente di 0°,
30°, 60°).
GNGTS – Atti del 23° Convegno Nazionale / 14.13
Come è evidente dalla Fig. 2 i contributi costruttivi alla costruzione
dell’immagine (zona di Fresnel) hanno la maggior parte dell’energia alle basse
frequenze, i contributi lontani dalla zona di Fresnel invece sono invece ad alta
frequenza. Un filtraggio passa-basso permette di mettere in evidenza le zone di
interesse. In seguito a questo filtraggio, un opportuno picking permette di limitare la
somma alle zone effettivamente costruttive determinando in pratica un’apertura
ottimale dell’operatore di migrazione. Ne risulta una diminuzione degli artefatti ed una
riduzione del rumore nell’immagine finale.
Fig. 2 - CRP (z,λ) con i segnali relativi alla linea tratteggiata (a) ed alla linea continua (c) e modulo
delle rispettive trsformate (b e d).
Sono state studiate le zone di Fresnel nel dominio degli angoli in profondità. A
partire da questo studio è stato proposto un algoritmo di filtraggio e picking nel
dominio angolare che permette un miglioramento qualitativo del risultato della
migrazione. Poiché nel dominio z,λ i contributi costruttivi sono quelli vicini alle
tangenze orizzontali si sta studiando la possibilità di un filtraggio FKλ che permetta di
diminuire la quantità di memoria necessaria.
Ringraziamenti. Gli autori sono grati a Nicola Bienati per aver suggerito il
problema ed a Diego Carotti per il calcolo dei limiti della zona di Fresnel nel dominio
angolare.
BIBLIOGRAFIA
Audebert F., Froidevaux P., Huard I., Nicoletis L. e Svay-Lucas J.; 2000: A multi-angle toolbox for
restored amplitude images and AVA-Gathers. 70th SEG exp. Abstracts, MIG 10.4.
Audebert F., Froidevaux P., Rakotoarisoa H. e Svay-Lucas J.; 2002: Insights in to migration in the
angle domain. 72th SEG exp. Abstracts, MIG 3.5.
Audebert F., Nicoletis L., Froidevaux P. e Rakotoarisoa H.; 2003:True-amplitude migration in the angle
domain by regularization of illumination. 73rd SEG exp. Abstracts, MIG 2.4.