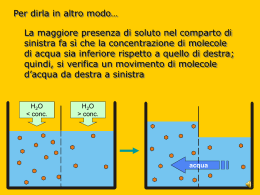
Diffusione e osmosi
Roberto Cirio
Corso di Laurea in Chimica e Tecnologia Farmaceutiche
Anno accademico 2007 – 2008
Corso di Fisica
La lezione di oggi
Sostanze sciolte in liquidi, se utilizzate con membrane,
hanno comportamenti particolari
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
2
Soluzioni
Diffusione
Membrane
L’osmosi
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
3
Un facile esperimento
•Bicchiere d’acqua
•Colorante
•Velocita’ iniziale del colorante = 0
Aspetto un
po’ di tempo
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
Arrivo a un
equilibrio
4
Soluzioni
Una sostanza viene disciolta in un liquido
Liquido Î solvente
Sostanza Î soluto
Solvente + soluto Î soluzione
Concentrazione molare (o molarita’): c = n/V
z
z
n: numero di moli di soluto
V: volume di solvente
Esempio: Qual’e’ la concentrazione molare di una soluzione formata di 2g di
saccarosio C12H22O11, disciolti in 100 cm3 di acqua ?
M(C12H22O11) = 12.(12) + 22.(1) + 11. (16) = 342 u.m.a.
n = 2/342 = 5.85.10-3 moli
c = n/V = (5. 85.10-3 moli)/(100.10-6 m3) = 58.5 moli/m3 = 5.85.10-2 moli/l
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
5
Soluzioni
Diffusione
Membrane
L’osmosi
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
6
Il moto delle molecole in una soluzione
Soluzione (solvente+soluto)
Ad esempio: acqua e zucchero
Parete divisoria
Solvente puro
Ad esempio: acqua
Fase 1: Le molecole di soluto urtano contro tutte le pareti
del recipiente (energia cinetica)
Energia cinetica delle molecole
3
K m = kT
2
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
7
Il moto delle molecole in una soluzione
Fase 2: Tolgo la parete divisoria
La linea tratteggiata indica la
posizione dov’era la parete
divisoria, che ora e’ stata tolta
Alcune molecole di soluto diffondono
nel lato destro del recipiente
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
8
Il moto delle molecole in una soluzione
La linea tratteggiata indica la
posizione dov’era la parete
divisoria, che ora e’ stata tolta
Fase 3
Alcune molecole di soluto diffondono nel lato destro del recipiente
Alcune molecole di soluto diffondono nel lato sinistro del recipiente
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
9
Il moto delle molecole in una soluzione
La linea tratteggiata indica la
posizione dov’era la parete
divisoria, che ora e’ stata tolta
Fase 4
Si e’ raggiunto l’equilibrio
La concentrazione e’ identica in entrambe le parti
Diffusione (sinistraÎdestra) = Diffusione (destra Îsinistra)
All’equilibrio,
non c’e’ flusso (molecole/(cm2 s))
di molecole nella soluzione
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
Φd-s = Φs-d
10
La legge di Fick
Vediamo la stessa cosa, in un modo diverso
cdestra < csinistra
Nel volume A.Δx arrivano piu’ molecole
da sinistra che da destra
Flusso netto (o risultante) da sinistra a
destra
Quando cdestra = csinistra, il flusso si ferma
Δx
Definisco J: velocita’ di diffusione:
z
z
Numero di molecole/s
Numero di moli/s
Legge di Fick
Diffusione e osmosi
Considero D, il coefficiente
diffusione e ottengo la
c1 - c 2
J =Corso
DAdi laurea in CTF
Δ2007/8
x
Fisica – a.a.
di
11
Coefficienti di diffusione
Diffusione e osmosi
Molecola
diffondente
Mezzo
D (m2/s)
H2
aria
6.3.10-5
O2
aria
1.8.10-5
O2
acqua
100.10-11
Emoglobina del
sangue
acqua
6.9.10-11
Glicina
(amminoacido)
acqua
95.10-11
DNA
(M=6.106 uma)
acqua
0.13.10-11
Corso di laurea in CTF
Fisica – a.a. 2007/8
12
Soluzioni
Diffusione
Membrane
L’osmosi
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
13
Membrane semipermeabili
Considero una membrana semipermeabile
z
z
z
z
z
z
Membrana
Forata
Diametro dei fori permette il passaggio di molecole piccole
Diametro dei fori evita il passaggio di molecole grandi
Esempio: lascia passare le molecole di acqua e blocca le molecole di
zucchero
Le pareti delle cellule e le superfici epiteliali sono semipermeabili
Molecole di H2O possono diffondere
verso destra e verso sinistra
Molecole di zucchero non possono
attraversare la membrana
semipermeabile
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
14
Membrane semipermeabili
Per la legge di Fick, si cerca di avere due
concentrazioni uguali
Non potendo aumentare la concentrazione a
destra, le molecole si muovono per diminuire la
concentrazione a sinistra
Ho un flusso da destra a sinistra (netto o
risultante)
Il volume di solvente a sinistra aumenta
Il livello a sinistra si alza rispetto al livello a destra
Perche’ ?
B
•In un certo istante, ho 10 molecole vicino ai fori
della membrana con la velocita’ diretta verso i fori
•Da A a B passano tutte le 10 molecole
•Da B ad A ne passano solo 6
A
Diffusione e osmosi
•Ho un flusso netto di 4 molecole da A a B
Corso di laurea in CTF
Fisica – a.a. 2007/8
•Statisticamente,
15
questo si rinnova continuamente
Soluzioni
Diffusione
Membrane
L’osmosi
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
16
L’osmosi
Osmosi: diffusione dell’acqua da una zona a bassa concentrazione verso una
zona ad alta concentrazione, attraverso una membrana semipermeabile
Il meccanismo e’ uguale a quello della diffusione libera
Voglio raggiungere un equilibrio nella concentrazione
Ma se utilizzo acqua pura, non riesco a raggiungere l’equilibrio
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
17
La pressione osmotica
Sono arrivato all’equilibrio
Posmotica = Pidrostatica
h
Posmotica mi e’ data dalla legge dei gas
perfetti, considerando il soluto come un
gas
nRT
Psoluto =
Equazione di
van ‘t Hoff
V
• la costante δ: coefficiente di dissociazione elettrolitica, e’
il rapporto tra particelle di soluto in soluzione e molecole
di soluto indissociato
•Se non si dissocia: δ=1
Posmotica = δ c R T
•Se si dissocia completamente (1 molecola, 2 ioni):
δ=2
•c: concentrazione del soluto
Diffusione e osmosi
•T:
Corso di laurea in CTF
Fisica
temperatura
in–Ka.a. 2007/8
18
Esercizio
Problema. In un osmometro e’ contenuta una soluzione diluita di saccarosio
(C12H 22O 11) ottenuta disciogliendo 1.0 g di zucchero in 1 l di acqua. Una volta
immerso l’osmometro in acqua pura, qual’e’ il dislivello che si determina a 20 C
in condizioni di equilibrio ?
M(C12H 22O 11)=12.(12)+22.(1)+11.(16)=342
n=(1.0)/(342)=2.9.10-3 moli
Posmotica = δ c R T =
(2.9⋅10-3 ) moli/l
= (1)
(8.31) ⋅ (273 + 20) =
−3
3
10 m /l
= 7.1 ⋅ 10 3 Pa
Membrana
semipermeabile
Diffusione e osmosi
Posmotica
7.1 ⋅ 10 3
h=
=
=0.72 m
3
ρg
(10 ) ⋅ (9.81)
Corso di laurea in CTF
Fisica – a.a. 2007/8
19
L’osmole
Una unita’ di misura pratica e’ l’osmole
1 osmole: 1 mole di soluto non elettrolita (δ=1)
La Posmotica di 1 osmole disciolta in 1 l di H2O a T=0 C e’:
1
6
)
⋅
(
8
.
31
)
⋅
(
273
)
=
2
.
27
⋅
10
Pa = 22.4 atm
−3
10
P = δ c R T = (1) ⋅ (
L’osmolalita’
Prendo un solvente
Sciolgo nel solvente vari tipi di soluto
Quale sara’ la concentrazione ?
c sara’ la concentrazione di tutte le molecole che non
diffondono attraverso la membrana
Corso di laurea in CTF
Diffusione
e osmosi in osmole/litro
Fisica – a.a. 2007/8
Si misura
20
Le soluzioni isotoniche
Ho un fenomeno osmotico quando e’ presente una membrana
semipermeabile che separa due soluzioni a c diversa
Il flusso di solvente va dalla c piu’ piccola alla c piu’ grande
Lo scopo e’ di uniformare le due c
Se tra i due comportamenti c’e anche una Δpidraulica, si deve
tener conto anche di questa
Due soluzioni con uguale c si dicono isotoniche
Con soluzioni isotoniche, Δposmotica = 0
Ogni sostanza iniettata nel sangue deve essere isotonica al
plasma, per evitare:
z
z
Flusso di solvente da cellule a plasma (atrofizzazione delle cellule) con
soluzione ipertonica (csoluzione > cplasma)
Flusso di solvente da plasma a cellule (le cellule si gonfiano ed
eventualmente si rompono; fenomeno dell’emolisi) con soluzione
ipotonica (csoluzione < cplasma)
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
21
Esempio
Problema. Qual’e’ la pressione osmotica del fluido intracellulare che ha
un’osmolalita’ di 0.30 osmoli/l alla temperatura corporea di 37 C ?
⎞
5
-1
Posmotica=cRT= ⎛⎜ 0.30-osmoli
7.73
⋅
10
Pa = 7.6 atm
⋅
⋅
+
=
(8.31
J
K
)
(273
37
K)
⎟
3
3
⎝ 10 m
⎠
Nella realta’ la Posmotica cellulare dipende dalla rigidita’ della parete
cellulare e dalla osmolalita’ del fluido che circonda la cellula
Problema. Calcolare la quantita’ di glucosio (C6H12O6) da sciogliere in 1 l di
acqua per ottenere una soluzione isotonica.
Voglio ottenere una osmolalita’ di 0.30 osmoli/l
M C 6 H12 O 6 = 6 ⋅ (12) + 12 ⋅ (1) + 6 ⋅ (16) = 180
m C 6 H12 O 6 = (0.3) ⋅ (180 g) = 54 g
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
22
Riassumendo
La diffusione e’ un fenomeno semplice
Membrane e soluzioni
permettono il funzionamento
di molti aspetti della fisiologia
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
23
Esercizio da svolgere a casa
n. 17.14 pag. 106 Celasco-Panzieri. 2000 problemi di fisica-ECIG
In un osmometro come illustrato in figura, viene immessa una soluzione di densita’
incognita. La membrana semipermeabile situata sul fondo dell’osmometro, si trova ad
una profondita’ h2 = 60 cm sotto il pelo libero del solvente puro.All’istante iniziale la
differenza di pressione attraverso la membrana e’ 0 e l’altezza della soluzione
nell’osmometro e’ h1=10 cm. Alla fine la soluzione raggiunge il valore h3= 80 cm.
Determinare:
1.
2.
3.
Diffusione e osmosi
La densita’ della soluzione all’istante iniziale
se la densita’ del solvente puro e’ ρ=103 kg/m3
La pressione osmotica della soluzione
La concentrazione della soluzione, nell’ipotesi
che la densita’ della soluzione alla fine
dell’esperimento sia praticamente invariata
rispetto alla densita’ iniziale e che la
temperatura sia 27 C.
Corso di laurea in CTF
Fisica – a.a. 2007/8
24
Soluzione
1 domanda
Se ΔP=0, allora le pressioni idrostatiche sono uguali.
Psolvente = ρ solvente g h 2
Psoluzione = ρ soluzione g (h 2 - h 1 )
Psoluzione = Psolvente
ρ soluzione
ρ solvente g h 2
(10 3 )( 9 . 8 )( 0 . 6 )
=
=
= 1 . 2 ⋅ 10 3 kg m 3
g (h 2 - h 1 )
(9.8)(0.6 - 0.1)
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
25
Soluzione
2 domanda
All’equilibrio, la pressione osmotica deve essere uguale alla pressione
idrostatica
Posmotica = ρ soluzione g h 3 = (1.2 ⋅ 10 )(9.8)(0.8) = 9.4 ⋅ 10 Pa
3
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
3
26
Soluzione
3 domanda
Posmotica = c R T
Posmotica
9.4 ⋅ 10 3
c =
= 3.78 moli/m3
=
RT
(8.31)(273 + 27)
Diffusione e osmosi
Corso di laurea in CTF
Fisica – a.a. 2007/8
27