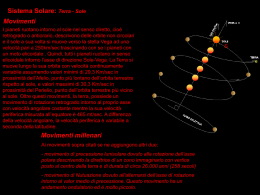
L’EQUILIBRIO UNIVERSALE
dalla meccanica celeste alla fisica nucleare
Cap.4 – giroscopio, magnetismo e forza di Lorentz
– teoria del giroscopio
Abbiamo finora preso in considerazione le condizioni di equilibrio dei sistemi
legati, imponendo nello spazio fisico il principio di conservazione dell’energia
solo sul piano orbitale.
Nell’universo che ci circonda si osservano però dovunque aggregati materiali
rotorivoluenti, variamente orientati nello spazio, i quali producono importanti
e vistosi effetti giroscopici che si manifestano in tutte le direzioni.
Per un’analisi più completa dell’equilibrio dei sistemi reali non si può dunque
non tenerne conto.
Noi non tratteremo la teoria generale del giroscopio, ma ci limiteremo a fare
solo i richiami necessari e sufficienti per la comprensione dei processi che
andremo a descrivere.
Con riferimento alla figura, consideriamo il moto di un punto matriale intorno
al centro O, assunto come origine di una terna di assi cartesiani X– Y– Z
fissi nello spazio.
Consideriamo ancora un’altra terna di assi ξ – η – ζ con la stessa origine O,
93
1
solidali con il punto P e dunque in moto con esso attorno all’origine O.
Sappiamo che, in generale, il momento angolare associato alla rotazione di
un corpo di forma qualsiasi, calcolato come somma vettoriale dei momenti di
tutti i suoi punti, non risulta parallelo all’asse di rotazione.
Qualunque sia la forma considerata, esistono tuttavia sempre tre assi tra loro
perpendicolari tali che, se il corpo ruota attorno ad uno di essi, il momento
angolare totale risulta parallelo all’asse di rotazione.
Questi assi vengono chiamati " assi principali di inerzia " ed i corrispondenti
momenti di inerzia sono indicati come " momenti principali di inerzia ".
Gli assi principali d’inerzia formano un sistema di riferimento solidale con il
corpo preso in considerazione e ruota con esso.
Dato che gli assi principali d’inerzia coincidono con gli assi di simmetria dei
corpi materiali e visto che nei casi reali, quasi sempre, la rotazione avviene
attorno ad un asse di simmetria, esamineremo questo caso particolare.
Per poter definire l’orientamento nello spazio del punto materiale considerato,
avente gli assi d’inerzia coincidenti con quelli mobili, sarà necessario riferire
questi ultimi agli assi fissi.
Se consideriamo "la linea dei nodi" di versore N , perpendicolare a entrambi
gli assi OZ e Oζ e orientata nel verso del prodotto esterno
possibile utilizzare gli angoli di Eulero, definiti come segue.
kΛν
, sarà
angolo di precessione ψ :
ψ = XO N
è l’angolo di cui deve ruotare l’asse
OX per poter coincidere
O N , attraverso una rotazione antioraria rispetto ad un
osservatore parallelo e concorde con l’asse OZ. Tale angolo può assumere
con la linea dei nodi
qualunque valore positivo o negativo.
angolo di nutazione
ϑ:
ϑ = ZOζ
è l’angolo formato dagli assi
è compreso tra 0 e π.
OZ
e
Oζ , che, per definizione,
94
2
ϕ:
angolo di rotazione propria
ϕ = NO ζ
è l’angolo di cui deve ruotare la linea dei nodi, di versore
N,
Oζ , attraverso una rotazione antioraria
rispetto ad un osservatore parallelo e concorde con l’asse Oζ.
per portarsi a coincidere con l’asse
Anche questo angolo può assumere qualunque valore positivo o negativo.
k Λ ν = N ⋅ senϑ
In base a queste definizioni, risulta :
Possiamo, a questo punto, esprimere la rotazione istantanea ω in funzione
degli angoli di Eulero, osservando che la posizione generica assunta dalla
terna di assi mobili O ξ η ζ , caratterizzata da tre valori arbitrari degli angoli
di Eulero ψ, ϑ, ϕ, può essere pensata ottenuta a partire dalla terna fissa
O x y z , mediante tre successive rotazioni attorno ad assi concorrenti
nello stesso punto fisso O , in ciascuna delle quali varia uno solo dei
suddetti angoli di Eulero. Si avrà dunque :
Una prima rotazione
⋅
ω1 = ψ k
Oζ
Questa operazione lascia l’asse
porta
Oξ
L’asse
attorno all’asse fisso O z.
coincidente con l’asse
Oη
verrà ad assumere di conseguenza una ben precisa posizione
O xy
, ruotata dello stesso angolo
⋅
Una seconda rotazione
ω2 = ϑ N
ψ
rispetto all’asse
Oη
*
Oζ
nella sua
verrà ad assumere di conseguenza una ben precisa posizione
nel piano delle rette
N
O y.
attorno alla linea dei nodi N, che lascia
l’asse O ξ coincidente con la linea dei nodi e porta l’asse
posizione finale.
versore
mentre
a coincidere con la linea dei nodi.
sul piano fisso
L’asse
Oz
Oz
e
O ζ , che in figura abbiamo caratterizzato con il
.
una terza rotazione
⋅
ω 3 = ϕ ν attorno all’asse O ζ , che porta gli assi O ξ
95
3
Oη ad assumere le loro rispettive posizioni finali, caratterizzate dai due
versori λ e μ contenuti nel piano passante per l’orine O e parallelo ai due
ed
versori
N
e
N
*
e ruotati, rispetto a questi ultimi, dello stesso angolo
Le tre rotazioni, concorrenti in
nell’unica rotazione :
ϕ.
O che abbiamo indicato si compongono così
⋅
⋅
⋅
ω = ψk + ϑN + ϕν
Le componenti della rotazione istantanea
con il corpo considerato
Oξηζ
ω
secondo gli assi mobili solidali
è dato dai prodotti scalari :
p=ω x
λ
q=ω xμ
s=ωxν
Per raggiungere il nostro scopo, calcoliamo, a questo punto, separatamente
il contributo che viene fornito a p, q, s dalle tre rotazioni
Per quanto riguarda
ω1 , ω2 , ω3 .
ω 1 , conviene realizzare una scomposizione preliminare
secondo le direzioni dei versori
⋅
N
*
e ν , complanari con essa :
⋅
ω1 = ψ k = ψ ⋅
*
senϑ N + cosϑ ν
96
4
con riferimento alla figura, scomponiamo ora il primo termine
secondo le direzioni
λeμ,
senϑ N
*
che sono complanari con esso :
*
senϑ N = senϑ ⋅ senϕ λ + cosϕ μ
in definitiva si ha quindi :
⋅
⋅
ω1 = ψ k = ψ ⋅
senϑ ⋅ senϕ λ + senϑ ⋅ cosϕ μ + cosϑ ν
Riguardo alla rotazione ω 2 conviene scomporla secondo le direzioni dei due
versori
λ
e
μ
che risultano complanari con essa :
⋅
⋅
ω2 = ϑ N = ϑ ⋅
La terza rotazione
cosϕ λ + senϕ μ
ω 3 non necessita di alcuna scomposizione e risulta :
⋅
ω2 = ϕ ν
si hanno dunque le componenti :
⋅
p=
ψ ⋅ senϑ ⋅ senϕ
q=
ψ ⋅ senϑ ⋅ cosϕ
⋅
s=
⋅
ψ ⋅ cosϑ
⋅
+
ϑ ⋅ cosϕ
–
ϑ ⋅ senϕ
+
ϕ
⋅
⋅
In alcuni problemi può risultare comodo calcolare le componenti di ω rispetto
*
alla terna di versori N , N , ν , anche se essa non è solidale con il sistema
rigido in esame.
Indicando queste componenti con p ∗ , q ∗ , s ∗ , si avrà :
97
5
∗
p =ω xN
∗
q =ω xN
*
∗
s =ωxν
Sostituendo le relazioni che sono state ricavate, si ottiene :
∗
p =
∗
q =
∗
s =s=
⋅
ϑ
⋅
ψ ⋅ senϑ
⋅
ψ ⋅ cosϑ
+
⋅
ϕ
La rotazione istantanea ω si potrà dunque scrivere :
⋅
⋅
⋅
*
ω = ψ k + ϑ N + ϕ ν = p ∗ N + q ∗ N + sν
Il momento risultante delle quantità di moto
K
rispetto al punto fisso
O vale :
*
K = I 1 ⋅ p λ + I 2 ⋅ p μ + I 3 ⋅ s ν = I 1 ⋅ p ∗ N + I 2 ⋅ q ∗ N + I 3 ⋅ sν
in cui
I1 , I2 , I3
versori
rappresentano i momenti principali d’inerzia con i rispettivi
λ, μ,ν.
Particolarmente diffuso è il caso in cui il corpo considerato ruota attorno a un
asse di simmetria I, mentre per gli altri due risulta
I 1 = I 2 = J.
Si ha così, per il momento risultante delle quantità di moto
K=J⋅
p
∗
N + q∗N
*
K , l’espressione :
+ I ⋅ sν
98
6
Per ricavare la condizione di equilibrio del solido considerato, applichiamo, a
questo punto, il teorema del momento risultante della quantità di moto rispetto
al punto fisso O.
E’ però da tener conto che la terna stereonodale non è animata dalla velocità
di rotazione ω , ma dalla :
⋅
⋅
⋅
ω* = ψ k + ϑ N = ω – ϕ ν
risulta dunque :
dK
=J ⋅
⋅
∗
p
⋅
N + q∗ N
⋅
*
+I ⋅s
dt
N
⋅
ω * Λ K = ω −ϕ ν ΛK =
p
J⋅
=
I–J
∗
∗
⋅
⋅q ⋅s+J⋅q ⋅ϕ
N
∗
p
q
∗
N–
J⋅
ν + ω*Λ K
*
ν
∗
q
s–
∗
I–J
⋅
=
ϕ
I⋅
∗
s
∗
⋅
⋅p ⋅s+J⋅p ⋅ϕ
N
*
Il momento risultante, rispetto al punto O, delle forze esterne si potrà scrivere
M = M NN + M N* N
*
+ Mν ν
dovendo, per avere equilibrio dinamico, soddisfare la relazione :
dK
dt
=M
si ricava il sistema di tre equazioni che esprime la condizione di equilibrio su
99
7
ciascuno dei tre assi :
⋅
J ⋅ p∗
I–J
⋅s+J⋅ϕ
–
I–J
⋅s+J⋅ϕ
⋅
J ⋅ q∗
⋅
+
∗
= MN
∗
= M N*
⋅q
⋅
⋅p
⋅
I ⋅ s = Mν
oppure, sostituendo a p ∗ , q ∗ , s le loro espressioni :
⋅⋅
J⋅ϑ +
J⋅
d
I–J
⋅
⋅
⋅ ψ ⋅ cosϑ + I ⋅ ϕ
⋅
ψ ⋅ senϑ
⋅
I–J
–
⋅ ψ ⋅ senϑ
⋅
= MN
⋅
⋅ ψ ⋅ cosϑ + I ⋅ ϕ
dt
I⋅
d
⋅
ψ ⋅ cosϑ
+
dt
⋅
⋅ϑ
= M N*
⋅
ϕ = Mν
Il caso più frequente in astronomia e in fisica atomica è quello in cui si potrà
assumere :
ϑ = ϑ 0 = costante
⋅
ψ = ω n = velocità di rivoluzione = costante
⋅
⋅
s = ψ ⋅ cosϑ + ϕ = ω p = velocità di rotazione = costante
Mν = 0
Si ottiene così :
;
⋅⋅
M N* = 0
;
⋅
ϑ=ϑ=0
e quindi:
⋅
M = I⋅ϕ + I–J
⋅
⋅ ψ ⋅ cosϑ
⋅
⋅ ψ ⋅ senϑN
ricordando infine la relazione :
100
8
N=
si ha :
⋅
⋅
M = I ⋅ ψ ⋅ cosϑ + ϕ
kΛν
senϑ
⋅
– J ⋅ ψ ⋅ cosϑ
⋅
⋅ψ ⋅
kΛν
e quindi, in definitiva :
M = I ⋅ ω p ⋅ ω n – J ⋅ ω 2n ⋅ cosϑ
⋅
kΛν
Questa relazione è fondamentale per lo studio di qualsiasi corpo rigido
rotorivoluente, in quanto descrive tutte le condizioni che consentono
l’equilibrio con lo spazio fisico.
Per chiarire quanto abbiamo finora visto, consideriamo una sfera di raggio r p
rotante su se stessa con velocità periferica v p e rivoluente con velocità
alla distanza
Vn
R n da un punto fisso O.
Per il momento d’inerzia si ha :
I=J=
2
5
2
⋅ mp ⋅ rp.
F = F ν la forza che agisce sulla sfera il suo momento
rispetto al punto fisso O sarà :
Se indichiamo con
M = F Λ R = F ⋅ R ⋅ senϑ
⋅k
Λν
La condizione di equilibrio diventa quindi :
F ⋅ R ⋅ senϑ =
2
5
⋅ mp ⋅ rp ⋅ ωn ⋅
2
ω p – ω n ⋅ cosϑ
Se l’asse di rotazione e quello di rivoluzione sono tra loro perpendicolari, si
ha
ϑ=
π
ed il momento assume il valore massimo :
2
F⋅R =
2
5
⋅ mp ⋅ rp ⋅ ωn ⋅ ωp
2
101
9