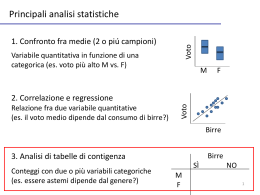
Analisi bivariata
Passiamo allo studio delle relazioni tra variabili
Andremmo a cercare se esiste una relazione tra due o più variabili, cioè se
esiste una variazione concomitante tra i valori, una COVARIAZIONE, ad
esempio al variare del titolo di studio varia il reddito.
Si tratta di una relazione statistica probabilistica: l’affermazione al crescere
del titolo di studio cresce il reddito vale in termini medi. Noto che c’è
questa relazione ma possono esserci eccezioni (sicuramente nei casi
studiati avrò degli individui che si comportano in modo diverso) ma, in
media, la relazione regge.
Si tratta di una relaziona causale, di tipo causa effetto. La statistica ci dice
soltanto che esiste una relazione, sta al ricercatore definire, dove
possibile, la relazione di causa ed effetto.
Tipi di relazioni tra variabili
Una variabile è detta esplicativa o indipendente se spiega o
influenza le variazioni di una variabile dipendente
Si parla di dipendenza logica tra due o più caratteri quando tra
questi sono ipotizzabili relazioni di causa ed effetto
Si parla di indipendenza logica quando tra due o più caratteri
si presuppone a priori con non può esistere nessuna
relazione di causa effetto.
L’analisi delle dipendenza studia come le modalità di un
carattere dipendano da un altro carattere. Il legame tra i
caratteri è unidirezionale o asimmetrico
L’analisi dell’interdipendenza studia come le modalità di un
carattere variano al variare di un altro carattere. Il legame
tra i due caratteri è bidirezionale o simmetrico.
Tabelle di contingenza
Per studiare la relazione tra 2 variabili iniziamo facendo
una tabella di contingenza, o tabella a doppia entrata, o
incrocio, o tabella doppia
La colonna e la riga dei totali si chiama: FREQUENZA
MARGINALE
r x c è l’ORDINE della tavola e sta indicare il numero di
righe per il numero di colonne
La DIMENSIONE della tavola indica il numero di variabili
coinvolte (a 2 dimensioni, a 3 …)
Si calcolano poi la percentuale di riga, la percentuale di
colonna e la percentuale sul totale
Tabelle di contingenza
QUALE % scegliere?
Se sto cercando di cogliere la relazione tra due variabili
esiste una regola:
Si sceglie la % di colonna quando si vuole analizzare
l’influenza che la variabile posta in colonna ha sulla
variabile posta in riga
Si sceglie la % di riga quando si vuole analizzare l’influenza
che la variabile posta in riga ha sulla variabile posta in
colonna
Tabelle di contingenza
E se vogliamo esaminare i profili di un fenomeno?
Possiamo confrontare i valori delle % di riga e di colonna
con i valori delle % marginali
Tabella di contingenza
y1
y2
…
yj
…
yc
totale
x1
n11
n12
…
n1j
…
n1c
n10
x2
…
xi
…
n21
…
ni1
…
n22
…
ni2
…
…
…
…
…
n2j
…
nij
…
…
…
…
…
n2c
…
nic
…
n20
…
ni0
…
xr
nr1
nr2
…
nrj
…
nrc
nr0
totale n01
n02
…
n0j
…
n0c
n
Tabelle di contingenza
Costruzione secondo alcuni criteri
PARSIMONIOSITA’ – riportare solo le % che servono
TOTALI – riportare sempre i totali di riga e di colonna (in
% o in valore assoluto)
BASI DELLE % - se riporto solo le % è meglio riportare
anche i totali (N) sui quali è calcolata la % - sotto un
numero ragionevole di unità N non ha senso calcolare
le %
CIFRE DECIMALI– sono previsti arrotondamenti e
riporto di 1 o al massimo 2 cifre decimali
INTESTAZIONE – le tavole devono essere sempre
intestate
Test del chi-quadrato
Esiste un criterio oggettivo per dire che tra due variabili esiste
o non esiste una relazione?
Sì per tabelle di contingenza di un campione sufficientemente
grande (N>100) è ed il testo del chi-quadrato χ2
Il test del χ2 si utilizza in presenza di caratteri qualitativi
nominali ma può essere applicato a caratteri qualitativi
ordinali o quantitativi divisi in classi
Test del chi-quadrato
Test statistico di verifica delle ipotesi – il primo passo è
formulare una ipotesi, chiamata ipotesi nulla o H0 secondo
la quale nella popolazione non esiste una relazione tra le
variabili e cercheremo di dimostrare con i dati che questa
ipotesi è falsa, non è compatibile con i nostri dati
Se l’ipotesi nulla H0 viene respinta, automaticamente
accettiamo l’ipotesi alternativa o ipotesi di ricerca H1 che
sostiene l’esistenza della relazione.
Se tra le 2 variabili della tabella di contingenza non ci fosse
relazione (ci fosse indipendenza) come sarebbero le
frequenze della tavola?
Frequenze attese
Dobbiamo costruire la tabella teorica di frequenze attese in caso di
assenza di relazione tra le 2 variabili
Nell’esempio, in caso di assenza di relazione, l’età non influirebbe sulla
propensione al viaggio
Questo accade quando le percentuali di chi viaggia e di chi non viaggia
sono uguali nelle tre classi d’età e quindi sono uguali a quanto accade in
tutta la popolazione della tavola
nij = frequenza congiunta della cella di incrocio tra la variabile Xi e la
variabile Yi
ni0 = frequenza marginale della variabile Xi
n0j = frequenza marginale della variabile Yi
nij attesa = ( ni0 * n0j ) / n
Test del chi quadrato
L’indice chi-quadrato χ2
misura la distanza della distribuzione di frequenza osservata dalla
distribuzione di frequenza attesa che si avrebbe in caso di indipendenza
Tale distanza è funzione delle differenze tra le frequenze osservate e quelle
teoriche e sono pari a
cij = nij - nij attesa
χ2 = ∑ c2ij / nij attesa
All’aumentare degli scarti in valore assoluto fra le frequenze osservate e
quelle teoriche il χ2 aumenta. L’indice è nullo quando le frequenze
osservate sono uguali a quelle attese e sono in un caso di indipendenza
Test del chi quadrato
Quanto deve essere grande il χ2 per poter dire con ragionevole certezza che
la distribuzione osservata presenta una associazione? Potrebbe capitare
che l’associazione tra le variabili sia da attribuire ad errori casuali….
La statistica ci dice quanto un certo valore del chi quadrato è
sufficientemente piccolo da poter essere attribuito ad errori casuali e
quindi pur non essendo = 0 è tuttavia compatibile con l’ipotesi nulla
(H0) di indipendenza tra variabili
La statistica ci dice per ogni valore del chi quadrato qual è la probabilità
che esso derivi da una popolazione con indipendenza. Se troviamo una
prob= 0,50 (50%) non possiamo respingere l’ipotesi nulla di
indipendenza
Anche se troviamo una prob = 0,10 (10%) non possiamo respingerla
Per convenzione si respinge l’ipotesi nulla di indipendenza se p<= 0,05,
cioè se il valore del chi quadrato è così grande da avere solo il 5% o
meno di probabilità di essere dovuto al caso
Test del chi quadrato
Questi valori di riferimento si trovano sulle tavole del chi-quadrato o
vengono stilati dai calcolatori
Le tavole sono riferite ai gradi di libertà di una distribuzione
Gradi di libertà = gl = (numero di righe -1)*(numero di colonne – 1)