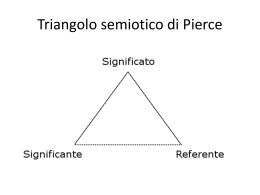
!"#"$#"!%
&'()*+,-.)'.%/.%0.12*3--,%02.%
+,43*.,5.%20,6%'35573083*.3'-,%/.%
8)5,*.+34*.,%
"%
9%
"%
!"#"$#"!%
!%
:%
9%
!"#"$#"!%
Caratteristiche
Classe 2: questi laser non possono causare danni agli occhi in
circostanze normali, possono provocare danni solo se a contatto con
gli occhi per un lungo periodo di tempo. La classe 2 dei laser opera
solo nel range visibile (400 – 700 nm) e ha un potere di uscita uguale
o inferiore di 1 mW.
Informazioni di Sicurezza per laser di Classe 2
Classificazione: per tutti i sistemi laser deve essere nota la classe. La
classificazione è certificata dal costruttore ovvero dal Responsabile se si tratta di
sorgente prototipo. Qualora il laser sia modificato il Responsabile deve curare la
riclassificazione del sistema.
Etichettatura: ogni laser deve essere provvisto di opportune targhette che
riportino la classe e la segnalazione delle aperture da cui emerge la radiazione.
Precauzioni di base sul fascio: non osservare il fascio direttamente
;%
<213%8)5,*.--,4,%.'%)=1,%3%
083>*)01)8.,%
<?@A%/.%BC&D&B?%E&F&B?%!%%
?A?A%9$"!G9$":%
H5.0,I3>,%B)55.'.%
35.0,I3>,A1)55.'.J2'.8/A.4%
K%
!%
!"#"$#"!%
"A! M3N'.-.)'3%/.%5213%8)5,*.--,4,%
9A! M.08)0.6O.%83*%.5%1)'4*)55)%/.%5213%8)5,*.--,4,%
%
!A! F83>*)01)8.,%1)'%5213%8)5,*.--,4,%
:A! P)43*3%)=1)%*)4,4)*.)Q%3083*.3'-,%/.%
5,I)*,4)*.)%
L%
R%
:%
!"#"$#"!%
!"#$%&'()*+#,-*()%.'/#*%0123#/'4&%5-&#
%
F4,*6'T%(*)+%D,UV35570%O.3V%)(%5.TW4%,0%,'%35314*)+,T'361%V,O3Q%)01.55,6'T%
35314*.1% N35/% ,'/% )01.55,6'T% +,T'361% N35/% V.4W% 4W3% 0,+3% (*3X23'1Y% I24%
)*.3'43/%83*83'/.125,*%
%
<.'3,*% 8)5,*.-3/% 5.TW4Q% 35314*.1% N35/% O314)*% )01.55,430% .'% ,+85.42/3% V.4W%
(*3X23'1Y%O%I24%,5V,Y0%8).'6'T%,5)'T%4W3%ZU%)*%[U%/.*316)'0Q%
E(z, t) = E x0 sin [ 2!" t ! 2! z / ! + "0 ]
?+85.42/3%)(%4W3%35314*.1%N35/%
8*)8,T,6'T%,5)'T%-%,'/%5.'3,*5Y%
8)5,*.-3/%,5)'T%4W3%U%/.*316)'%
S%
!"! $%&'()*+#,-*()%.'/#*%0123#/'4&%5-&#
E(z, t) = E x0 sin [ 2!" t ! 2! z / ! + "0 ]
P)5,*.-3/%
5.TW4%,5)'T%U%
,U.0%
%
%
E(z, t) = E y0 sin [ 2!" t %! 2! z / ! + "0 ]
%
P)5,*.-3/%
5.TW4%,5)'T%Y%
,U.0%
%
%
"$%
;%
!"#"$#"!%
!"#$%&'()*+#,-*()%.'/#*%0123#/'4&%5-&#
%
%
P)5,*.-3/%
5.TW4%,4%:;\%
(*)+%U%,U.0%
%
%
%
%
P)5,*.-3/%
5.TW4%,4%!$\%
(*)+%U%,U.0%
%
%
""%
!"#$%&'()*+#,-*()%.'/#*%0123#0'&')(*%.(5-&#
%
<.'3,*%8)5,*.-3/%5.TW4%V.4W%.40%8)5,*.-,6)'%,U.0%)*.3'43/%.'%,'Y%/.*316)'%.'%4W3%UY%85,'3%
1,'%I3%4W)2TW4%,0%1)'0.06'T%)(%4V)%1)+8)'3'40%)*.3'43/%,5)'T%4W3%U%,'/%Y%,U30]%
*308316O35YA%%
%
%
0
0
% E = E x + E y = E x i + E y j sin 2 !" t ! 2 ! z / ! + " 0
%
%
{
} [
]
!"#$%&'$()$*+,-%."#$%/0".$1%
%
%20$%'$3"45$%#"6*78)9$%:&%80$%8;:%+:#/:*$*8.%9$8$'#7*$.%80$%/:3"'7<"4:*%
"=7.%:'7$*8"4:*%
%
"9%
K%
!"#"$#"!%
6%)67*()*+#,-*()%.'/#*%012#
%
F2+%)(%4V)%1)+8)'3'40%V.4W%./3'61,5%+,T'.42/30%H$%I24%S$\%)24%)(%8W,03Q%
Ercp = E 0 {sin [ 2!" t ! 2! z / ! + "0 ] i + sin [ 2!" t ! 2! z / ! + "0 + # / 2 ] j} =
= E 0 {sin [ 2!" t ! 2! z / ! + "0 ] i + cos [ 2!" t ! 2! z / ! + "0 ] j}
Elcp = E 0 {sin [ 2!" t ! 2! z / ! + "0 ] i + sin [ 2!" t ! 2! z / ! + "0 ! # / 2 ] j} =
= E 0 {sin [ 2!" t ! 2! z / ! + "0 ] i ! cos [ 2!" t ! 2! z / ! + "0 ] j}
"!%
6%)67*()*+#,-*()%.'/#*%012#
%
F2+%)(%4V)%1)+8)'3'40%V.4W%./3'61,5%+,T'.42/30%H$%I24%S$\%)24%)(%8W,03Q%
":%
L%
!"#"$#"!%
6%)67*()*+#(&/#*%&'()*+#,-*()%.'/#*%012#
%
%
B.*125,*5Y%8)5,*.-3/%5.TW4%^%1)+I.',6)'%)(%5.'3,*5Y%8)5,*.-3/%1)+8)'3'40%)24%)(%8W,03%
%
%
%
<.'3,*%8)5,*.-3/%5.TW4%^%1)+I.',6)'%)(%3X2,5%X2,'64Y%)(%*.TW4%,'/%53_%1.*125,*5Y%
8)5,*.-3/%1)+8)'3'40%
Ex =
Ercp + Elcp
= E 0 sin [ 2!" t ! 2! z / ! + "0 ] i
2
Ey =
Ercp ! Elcp
= E 0 sin [ 2!" t ! 2! z / ! + "0 ] j
2
";%
0'&')(*%.(5-&#
%
%
B)+I.',6)'%)(%4V)%5.'3,*5Y%8)5,*.-3/%V,O30%V.4W%0,+3%(*3X23'1Y%,'/%8W,03%I24%
/.`3*3'4%,+85.42/30Q%5.'3,*5Y%8)5,*.-3/%V,O3%V.4W%/.`3*3'4%8)5,*.-,6)'%,U.0%
)*.3'4,6)'%
%
B)+I.',6)'%)(%4V)%5.'3,*5Y%8)5,*.-3/%V,O30%V.4W%0,+3%(*3X23'1Y%,'/%,+85.42/3%I24%
)24%)(%8W,03Q%1.*125,*5Y%8)5,*.-3/%5.TW4%a53_%)*%*.TW4b%
%
B)+I.',6)'%)(%4V)%1.*125,*5Y%8)5,*.-3/%V,O30]%53_%,'/%*.TW4]%V.4W%0,+3%(*3X23'1Y]%
,+85.42/3%,'/%8W,03Q%5.'3,*5Y%8)5,*.-3/%5.TW4%%
%
D)*3%T3'3*,5%1,03Q%'**%,56(**+#,-*()%.'/#*%012%%
%
%
E = E x0 sin [ 2!" t ! 2! z / ! + "0 ] i + E y0 sin [ 2!" t ! 2! z / ! + "0 + " ] j
"K%
R%
!"#"$#"!%
8'&')(*%.(5-&%
%
E = E x0 sin [ 2!" t ! 2! z / ! + "0 ] i + E x0 sin [ 2!" t ! 2! z / ! + "0 + " ] j
"L%
9"#:';%6'<#=-)#6-&2)-*#-=#,-*()%.'/#*%012#
%
)2*%3Y30%,*3%8)5,*.-,6)'GI5.'/c%
%
G! <.'3,*%8)5,*.-3*0%a/.1W*).1]%I.*.(*,'T3'4]dbQ%4*,0+.4%,%I3,+%
)(% 5.TW4% VW)03% 35314*.1% N53/% O314)*% )01.55,430% .'% ,% 85,'3%%
4W,4%1)'4,.'0%4W3%I3,+%,U.0%a,50)%1,553/%85,'3%8)5,*.-3*0b%
%
G! e34,*/3*0Q% 1W,'T3% 4W3% *35,6O3% 8W,03% I34V33'% 4V)%
)*4W)T)',5%8)5,*.-,6)'%1)+8)'3'40%)(%5.TW4%%
%
G! M38)5,*.-3*0Q%4*,0()*+%8)5,*.-3/%5.TW4%.'%2'8)5,*.-3/%5.TW4%
%
"R%
S%
!"#"$#"!%
<.'3,*%8)5,*.-3*0%
"S%
9$%
"$%
!"#"$#"!%
&/3,5%8)5,*.-3*0Q%
!^$\%%Gf%"$$g%
!^S$\%%Gf%$g%
%
*3,5%8)5,*.-3*0Q%
!^$\%%Gf%%%%h"$$g%
!^S$\%%Gf%%f$g%
%
9"%
>(*7<?#*(@3#
%
%
%
%
%
%
%
%
%
%
%
I = I 0 cos2 ! i
%
VW3*3%&$%.0%4W3%.'.6,5%.'43'0.4Y]%,'/%%%%%%%%%%%%%%%%%%%%%%%%%%%.0%4W3%,'T53%
! i = !1 ! ! 0
I34V33'%4W3%5.TW4i0%.'.6,5%8)5,*.-,6)'%/.*316)'%,'/%4W3%,U.0%)(%
4W3%8)5,*.-3*A%
99%
""%
!"#"$#"!%
B.'3+,%!M%
9!%
F+,*48W)'30Q%
<2+.,%R$$]%<2+.,%S$$%3%j)k.,%HL%0)')%/)4,6%/.%2'%8,*61)5,*3%01W3*+)%l<HM%
/3')+.',4)%B53,*@5,1k%
9:%
"9%
!"#"$#"!%
W>8Q##VVVA'.k)'01W))5A.4%
9;%
P)5,*.-3/%02'T5,0030%
9K%
"!%
Both P5 and entropy are higher in the regions of
ered or multilayered interference, diffraction, zero and color, consisting of a regularly spaced lattice R/a, the system creates minimum-energy configuyellowish
but the
dark field.
With ofuse
of confocal
we by incorporating
rations formicroscopy,
the curved substrates
of features thatindistinguish
one species
beetle
order diffraction,
and border,
light scattering
(1–5)core
and disappears
greater curvature, revealing packing issues on
observe
that from
thesepigmentation
cells consist
arcs
onboundaries
the surface
of a(22–24). This results
grain
and defects
fromnearly
the other.concentric
In bright fieldnested
microscopy
(Fig.that
2), lie
often with
contributions
as of
curved
surfaces.
in the faceted to
morphology
viruses (22) and
the structureare
of C.
gloriosa seems
to consist
of analogous
well. The
complexity
of the
in part
shallow
cone.
Wepatterns
inferisthat
the patterns
structurally
and
optically
the focalof conic
The head, thorax, and abdomen of a beetle are
determined genetically, but the final development hexagonal cells (~10 mm), where each cell ap- grain boundary scars in colloidosomes (particles
domains
spontaneously
free
surface
of a yellow
cholesteric
These
textures
packedcrystal.
on a spherical
droplet)
(23). We canall
infer
pearsthe
to be
green
with a bright
core or liquid
and control
is related formed
to the conditions
during the on
curved, although the radius of curvature, R, is
provide
the basis
forThe
thephysical
morphogenesis
well as key
insights
for emulating
the intricate
optical
that the exoskeleton
of the beetle
possesses imnucleus. Weas
characterized
the extent
of hexagoformation
of the pattern
(10, 11).
large compared with the size of individual cells,
nal orderbeetles.
in patterns by using Voronoi analysis, perfect hexagonal, cellular pattern because sixfold
and chemical
aspectsof
of the
morphogenesis
can beof scarab
response
exoskeleton
a, or R/a >> 1. Although hexagonal packing prounraveled by studying the patterns in nature and which is a versatile method for pattern recog- triangulations or hexagons are not energetically
analyzing their analogs in equilibrium and non- nition and for modeling the properties of spatial favored everywhere.
vides the most efficient utilization of space on a
We examined the beetle exoskeleton with use
equilibrium patterns formed in condensed matter structures (21). Although the population of sixfor nearly a century plane, defects in coordination number are essenridescent beetles, butterflies, certain sea or- light has been investigated
(12–15). The quest for miniature optical devices sided polygons is the highest, there exist large of a laser scanning confocal microscope [Leica
tial for wrapping such tessellations on a sphere
(16–20),polygons.
since itIfwasTCS
firstSPreported
by Michelson
andto benefit
manyfrom
birds
their
color
DMR XE (Leica
Microsystems GmbH,
numbers
of fiveand seven-sided
and photonicsganisms,
is most likely
the derive
Wetzlar,
Germany)] and the
reconstructed
map For example, soccer balls and C60 (fulldefine
study of bioengineered
and organelles
of we
to represent(6).
the fraction
of n-sided
Recently
Goldstein
(7) summarized
history a 3D(22).
from theorgans
interaction
of light
with
thePnstructhe biological world. Rational design requires one polygons, we find that P5 decreased from 0.34 at of the underlying structure by using the autoture or morphology that is imprinted on their of optical measurements made in scarab beetles erenes) contain 12 pentagons in addition to the hexto understand how basic structural units interact
agons
that template the curved structure. Because
and
performed
ellipsometric
studies
confirming
exoskeletons
(1–5).
The
bright
and
varied
colors
of
with light and how they can be fabricated by
Fig. 1. Photographs of A
either self-assembly
or a top-down
beetles have
been of approach.
interest to scientists
6–8), (A) their polarizing behavior. TheBreflectance of the the beetle has a curved body, a certain number of
the beetle (2,
C. gloriosa.
In this context, we have been examining the
The bright history
green color, C. gloriosa beetle has a broad halo from 500 to
pentagons is expected, but the analysis reveals
but they also have a long and interesting
structure on the exocuticle of the beetle Chrysina with silver stripes as seen
“jewel gloriosa),
beetles,”
which
were in
used
in textiles 600 nm with two peaks at 530 (green) and 580 much higher disorder. According to Nelson (22),
gloriosaas
(or Plusiotis
which
selectively
unpolarized light or with
reflects left
circularly polarized
and posthe energetic cost associated with creating these
nm
(yellow),
respectively.
or ornaments
(9) inlight
many
Asiana countries.
The
left circular polarizer. (B)
sesses a brilliant metallic appearance (Fig. 1). If The green color is mostly
When the exoskeleton of the beetle is ob- 12 defects scales as YR2, where Y is the twostudy of photonics in nature reveals beautiful and
left circularly polarized light is blocked by the lost when seen with a right
served under an optical microscope, the body dimensional (2D) Young’s modulus. Because the
examples
ofasubwavelength
structural
use of adiverse
quarter wave
plate and
polarizer, as circular
polarizer. feashown intures
Fig. 1B,
beetle observed
loses its characterthatthecreate
colors through thin lay- appears as a richly decorated mosaic of cusps cost becomes substantial for systems with large
istic bright green reflection. The ability of certain
and color, consisting of a regularly spaced lattice R/a, the system creates minimum-energy configuered
or
multilayered
interference,
diffraction,
zero
species of beetles to reflect circularly polarized
I
1
order diffraction, and light scattering (1–5) and of features that distinguish one species of beetle
often with contributions from pigmentation as from the other. In bright field microscopy (Fig. 2),
well. The complexity of the patterns is in part the structure of C. gloriosa seems to consist of
determined genetically, but the final development hexagonal cells (~10 mm), where each cell apand control is related to the conditions during the pears to be green with a bright yellow core or
formation of the pattern (10, 11). The physical nucleus. We characterized the extent of hexago24 JULY 2009
order325
in patterns
by using Voronoi analysis,
and chemical aspects ofwww.sciencemag.org
morphogenesis can SCIENCE
be nal VOL
unraveled by studying the patterns in nature and which is a versatile method for pattern recoganalyzing their analogs in equilibrium and non- nition and for modeling the properties of spatial
equilibrium patterns formed in condensed matter structures (21). Although the population of six(12–15). The quest for miniature optical devices sided polygons is the highest, there exist large
five- and seven-sided polygons. If
and photonics is most likely to benefit1,2 from the 2,3numbers of 1,2
Vivek Sharma, Matija Crne, Jung Ok Park, Mohan Srinivasarao1,2,3
study of bioengineered organs
and organelles of we define Pn to represent the fraction of n-sided
the biological world. Rational
design requires
one beetle,
polygons,
we findwhich
that selectively
P5 decreased
0.34 at
The iridescent
metallic green
Chrysina gloriosa,
reflectsfrom
left circularly
polarized light,
possesses
an exoskeleton decorated by hexagonal cells (~10 mm) that coexist with
to understand how basic structural
units
interact
and
heptagons.by
The fraction of hexagons decreases with an increase in curvature. In
with light and how they pentagons
can
be
fabricated
bright field microscopy, each cellFig.
contains
yellow core,
1.a bright
Photographs
ofplaced
A in a greenish cell with
either self-assembly or a top-down
approach.
yellowish border,
but the core disappears in dark field. With use of confocal microscopy, we
the beetle C. gloriosa. (A)
observe
these cells consist
In this context, we have
beenthat
examining
the of nearly concentric nested arcs that lie on the surface of a
The
bright
green
color,
We infer that the patterns are structurally and optically analogous to the focal conic
structure on the exocuticle shallow
of the cone.
beetle
Chrysina
silver
stripes
seen liquid crystal. These textures
domains formed spontaneously onwith
the free
surface
of aas
cholesteric
gloriosa (or Plusiotis gloriosa),
selectively
providewhich
the basis
for the morphogenesis
as well aslight
key insights
in unpolarized
or withfor emulating the intricate optical
response of
the exoskeleton
reflects left circularly polarized
light
and pos-of scarab
a leftbeetles.
circular polarizer. (B)
sesses a brilliant metallic appearance (Fig. 1). If The green color is mostly
beetles,by
butterflies,
sea or- light has been investigated for nearly a century
left circularly polarized lightridescent
is blocked
the certain
losttheir
when
seen(16–20),
with a right
since it was first reported by Michelson
ganisms, and many birds derive
color
use of a quarter wave plate from
and the
a polarizer,
circular
polarizer.
(6). Recently Goldstein (7) summarized the history
interaction ofas
light with
the structure loses
or morphology
that is imprinted on their of optical measurements made in scarab beetles
shown in Fig. 1B, the beetle
its character(1–5).
bright and varied colors of and performed ellipsometric studies confirming
istic bright green reflection.exoskeletons
The ability
ofThe
certain
beetles have been of interest to scientists (2, 6–8), their polarizing behavior. The reflectance of the
species of beetles to reflect
but circularly
they also havepolarized
a long and interesting history C. gloriosa beetle has a broad halo from 500 to
School of Polymer, Textile, and Fiber Engineering, Georgia
Institute of Technology, Atlanta, GA 30332, USA. 2Center
for Advanced Research on Optical Microscopy (CAROM),
Georgia Institute of Technology, Atlanta, GA 30332, USA.
3
School of Chemistry and Biochemisty, Georgia Institute of
Technology, Atlanta, GA 30332, USA.
Structural Origin of Circularly Polarized
Iridescence in Jeweled Beetles
!"#"$#"!%
rations for the curved substrates by incorporating
grain boundaries and defects (22–24). This results
in the faceted morphology of viruses (22) and
grain boundary scars in colloidosomes (particles
packed on a spherical droplet) (23). We can infer
that the exoskeleton of the beetle possesses im449
perfect
hexagonal, cellular pattern
because sixfold
REPORTS
triangulations or hexagons are not energetically
the highly curved head to about 0.19 at the flattest
favored
region on everywhere.
the beetles’ back, whereas P7 is typithe beetle
exoskeleton
with use
callyWe
closeexamined
to 0.13 everywhere
else. Although
most
of the
pentagons
and heptagons
occur inmicroscope
clusters,
of
a laser
scanning
confocal
[Leica
there are finite numbers of pentagons that occur
TCS
SP
DMR
XE
(Leica
Microsystems
GmbH,
individually. The number and spatial distribution of
Wetzlar,
Germany)]
polygons characterizes
the and
spatialreconstructed
order. Entropy, a 3D map
S = the
–SPnlnP
was determined
for the auton, of the structure
of
underlying
structure
by using
each image. Whereas for perfectly ordered hexagons P6 = 1 and S = 0, the value of the entropy on
beetle exoskeleton varies between 0.85 and 0.95.
Both P5 and entropy
B are higher in the regions of
greater curvature, revealing packing issues on
curved surfaces.
The head, thorax, and abdomen of a beetle are
all curved, although the radius of curvature, R, is
large compared with the size of individual cells,
a, or R/a >> 1. Although hexagonal packing provides the most efficient utilization of space on a
plane, defects in coordination number are essential for wrapping such tessellations on a sphere
(22). For example, soccer balls and C60 (fullerenes) contain 12 pentagons in addition to the hexagons that template the curved structure. Because
the beetle has a curved body, a certain number of
pentagons is expected, but the analysis reveals
as “jewel beetles,” which were used in textiles 600 nm with two peaks at 530 (green) and 580 much higher disorder. According to Nelson (22),
1
the energetic cost associated with creating these
ornaments
(9) in many
Asian countries. The nm (yellow), respectively.
School of Polymer, Textile, and or
Fiber
Engineering,
Georgia
2
When the exoskeleton of the beetle is ob- 12 defects scales as YR2, where Y is the twophotonics
in nature
reveals beautiful and
Center
Institute of Technology, Atlanta,study
GA of
30332,
USA.
diverse examples of subwavelength structural fea- served under an optical microscope, the body dimensional (2D) Young’s modulus. Because the
for Advanced Research on Optical Microscopy (CAROM),
tures that create observed colors through thin lay- appears as a richly decorated mosaic of cusps cost becomes substantial for systems with large
Georgia Institute of Technology,ered
Atlanta,
GA 30332, USA.
or multilayered interference, diffraction, zero and color, consisting of a regularly spaced lattice R/a, the system creates minimum-energy configu3
School of Chemistry and Biochemisty,
Georgia Institute
order diffraction,
and light of
scattering (1–5) and of features that distinguish one species of beetle rations for the curved substrates by incorporating
Technology, Atlanta, GA 30332,often
USA.with contributions from pigmentation as from the other. In bright field microscopy (Fig. 2), grain boundaries and defects (22–24). This results
well. The complexity of the patterns is in part the structure of C. gloriosa seems to consist of in the faceted morphology of viruses (22) and
determined genetically, but the final development hexagonal cells (~10 mm), where each cell ap- grain boundary scars in colloidosomes (particles
to be green withVOL
a bright
yellow24
coreJULY
or packed
and control is relatedwww.sciencemag.org
to the conditions during the pearsSCIENCE
325
2009on a spherical droplet) (23). We can infer
formation of the pattern (10, 11). The physical nucleus. We characterized the extent of hexago- that the exoskeleton of the beetle possesses imand chemical aspects of morphogenesis can be nal order in patterns by using Voronoi analysis, perfect hexagonal, cellular pattern because sixfold
unraveled by studying the patterns in nature and which is a versatile method for pattern recog- triangulations or hexagons are not energetically
analyzing their analogs in equilibrium and non- nition and for modeling the properties of spatial favored everywhere.
We examined the beetle exoskeleton with use
equilibrium patterns formed in condensed matter structures (21). Although the population of six(12–15). The quest for miniature optical devices sided polygons is the highest, there exist large of a laser scanning confocal microscope [Leica
and photonics is most likely to benefit from the numbers of five- and seven-sided polygons. If TCS SP DMR XE (Leica Microsystems GmbH,
study of bioengineered organs and organelles of we define Pn to represent the fraction of n-sided Wetzlar, Germany)] and reconstructed a 3D map
the biological world. Rational design requires one polygons, we find that P5 decreased from 0.34 at of the underlying structure by using the autoto understand how basic structural units interact
with light and how they can be fabricated by
Fig. 1. Photographs of A
B
either self-assembly or a top-down approach.
the beetle C. gloriosa. (A)
In this context, we have been examining the
The bright green color,
structure on the exocuticle of the beetle Chrysina with silver stripes as seen
gloriosa (or Plusiotis gloriosa), which selectively in unpolarized light or with
reflects left circularly polarized light and pos- a left circular polarizer. (B)
sesses a brilliant metallic appearance (Fig. 1). If The green color is mostly
left circularly polarized light is blocked by the lost when seen with a right
use of a quarter wave plate and a polarizer, as circular polarizer.
shown in Fig. 1B, the beetle loses its characteristic bright green reflection. The ability of certain
species of beetles to reflect circularly polarized
I
1
449
9L%
A"#B,'62)-<6-,+#@%21#,-*()%.'/#*%012#
School of Polymer, Textile, and Fiber Engineering, Georgia
Institute of Technology, Atlanta, GA 30332, USA. 2Center
for Advanced Research on Optical Microscopy (CAROM),
Georgia Institute of Technology, Atlanta, GA 30332, USA.
3
School of Chemistry and Biochemisty, Georgia Institute of
Technology, Atlanta, GA 30332, USA.
www.sciencemag.org
SCIENCE
VOL 325
24 JULY 2009
449
9R%
":%
!"#"$#"!%
?0%3U,+853]%.(%V3%,*3%.'43*3043/%.'%,I0)*I,'13%+3,02*3+3'40]%4W3%<,+I3*4G
@33*%5,V%.0%O3*.N3/Q%
%
I
%
A = ! (" )CL = log10 0
%
I
%
%
%
mW,4%+,Y%1W,'T3%.(%V3%203%8)5,*.-3/%5.TW4n%
%
•! j)4W.'Tc%%.(%4W3%0,+853%.0%.0)4*)8.1%
•! M383'/0dA.(%4W3%0,+853%.0%,'.0)4*)8.1%a*308)'03%/383'/.'T%)'%4W3%
)*.3'4,6)'%)(%4W3%8)5,*.-,6)'%,U.0%b%
9S%
A|| = !|| (" )CL = log10
I 0,||
I
! log10 0," = !" (" )CL = A"
I||
I"
oW3%,I0)*86)'%)(%5.'3,*5Y%8)5,*.-3/%5.TW4%.0%*35,43/%4)%+)53125,*%04*2142*3%
4W*)2TW%4W3%0Y++34*Y%)(%4W3%V,O3%(2'16)'0%
!$%
";%
!"#"$#"!%
C,56(*#)-2(5-&#(&/#6%)67*()#/%61)-%<D3##
E1%)-F-,56(*##<,'62)-<6-,%'<#
#
%
B.*125,*%M.1W*).0+%aBMb^%/.`3*3'13%.'%,I0)*I,'13%I34V33'%53_%,'/%*.TW4%
1.*125,*5Y%8)5,*.-3/%5.TW4%
%
F+,55%3`314%
%
lj<p%1W.*,5%+)5312530%a,0Y++34*.1%+)5312530%4W,4%/)%')4%3UW.I.4%+.**)*%
0Y++34*Yb%
%
0,R
0,L
R
R
10
10
L
R
L
A = ! (" )CL = log
I
I
! log
I
= ! (" )CL = AL
I
!! = ! L " ! R
!"%
!9%
"K%
!"#"$#"!%
!!%
D)5312530% )861,55Y% ,16O3% % a)*% 1W.*,5b% 3UW.I.4% 6%)67*()# /%61)-%<D# ,'/% -,56(*#
)-2(5-&"##
mW3'% ,% 1.*125,*5Y% /.1W*).1% 0,+853% .'43*,140% V.4W% 5.'3,*5Y% 8)5,*.-3/% 5.TW4]% .4%
4*,'0()*+0%4W3%5.'3,*%8)5,*.-,6)'%.'4)%355.861,5%8)5,*.-,6)'A%
oW.0%W,883'0%I31,203%4W3%4V)%1.*125,*%1)+8)'3'40%)(%4W3%5.'3,*5Y%8)5,*.-3/%I3,+%
VW.1W% )*.T.',55Y% W,/% 3X2,5% ,+85.42/30% ,*3% ,I0)*I3/% IY% /.`3*3'4% ,+)2'40]%
*30256'T%.'%2'3X2,5%,+85.42/30%)(%4W303%1)+8)'3'40%.'%4W3%4*,'0+.>3/%5.TW4%%
E = E x0 sin [ 2!" t ! 2! z / ! + "0 ] i + E y0 sin [ 2!" t ! 2! z / ! + "0 + " ] j
oW3%355.861.4Y%)(%4W3%*30256'T%8)5,*.-,6)'%355.803%.0Q%
! CD = !" " C " L
!:%
"L%
!"#"$#"!%
l861,5% *)4,6)'Q% *)4,6)'% )(% 4W3% 8)5,*.-,6)'% 355.803% ,U.0% IY% ,'% )861,55Y% ,16O3% 02I04,'13]%
*30254%)(%1.*125,*%I.*3(*.'T3'13%
%
&'% ,% 1.*125,*5Y% I.*.(*,'T3'4% 0,+853% 4W3*3% .0% /.`3*3'13% .'% 4W3% .'/.130% )(% *3(*,16)'% ()*% 53_G
W,'/3/%a'<b%%,'/%*.TW4GW,'/3/%a'eb%1.*125,*5Y%8)5,*.-3/%5.TW4Q%%
%
%
L
R
%
mW3'% 8)5,*.-3/% 5.TW4% .'43*,140% V.4W% ,% 1.*125,*5Y% I.*.(*,'T3'4% 0,+853]% 4W3% *.TW4GW,'/3/%
1.*125,*% 1)+8)'3'4% .0% *34,*/3/% IY% ,'% ,+)2'4% /.`3*3'4% (*)+% 4W3% 53_GW,'/3/% 1.*125,*%
1)+8)'3'4]%*30256'T%.'%,%*)4,6)'%)(%4W3%8)5,*.-,6)'%355.803Q%
!n = n " n
!CB =
!L
"n
"
!;%
!n > 0, nL > nR
!n < 0, nL < nR
/3U4*,*)4,4)*Y% 8)5,*.-,6)'%355.803%*)4,43/%.'%
,% 15)1kV.03% 03'03% ,11)*/.'T% 4)% ,'% )I03*O3*%
5))k.'T%4)V,*/%4W3%5.TW4%0)2*13%
53O)*)4,4)*Y% 8)5,*.-,6)'% 355.803% *)4,43/% .'% ,%
1)2'43*15)1kV.03% 03'03% ,11)*/.'T% 4)% ,'%
)I03*O3*%5))k.'T%4)V,*/%4W3%5.TW4%0)2*13%
!K%
"R%
!"#"$#"!%
!L
"n
"
&'%*,/.,'0%
!CB =
!n = nL " nR
F831.N1%*)4,6)'%.'%/3T%/+G"%1+!%TG"%
%
%
D)5,*%*)4,6)'%.'%/3T%<%1+G"%+)5G"%
[!CB ]
[!CB ] M
F831.N1%*)4,6)'%,4%,%T.O3'%o%,'/%":#
T
[! ]!
!L%
H083*.3'-,%/.%5,I)*,4)*.)Q%
D.02*,%/35%8)43*3%)=1)%*)4,4)*.)%/.%0)52-.)'.%/.%-211W3*.%
!R%
"S%
!"#"$#"!%
G,,*%6(5-&<#
%
D,'Y%1W3+.1,50%3UW.I.4%,%0831.N1%*)4,6)'%,0%,%2'.X23%
8*)83*4YA%P)5,*.+343*0%1,'%./3'6(Y%2'k')V'%0,+8530%
I,03/%)'%4W.0%.(%)4W3*%O,*.,I530%021W%,0%1)'13'4*,6)'%,'/%
53'T4W%)(%0,+853%1355%53'T4W%,*3%1)'4*)553/%)*%,4%53,04%
k')V'A%%
B)'13'4*,6)'% ,'/% 82*.4Y% +3,02*3+3'40% ,*3% 30831.,55Y% .+8)*4,'4% 4)% /343*+.'3%
8*)/214%)*%.'T*3/.3'4%X2,5.4Y%.'%4W3%())/%q%I3O3*,T3%,'/%8W,*+,13261,5%.'/204*.30A%
F,+8530% 4W,4% /.085,Y% 0831.N1% *)4,6)'0% 4W,4% 1,'% I3% 1,5125,43/% ()*% 82*.4Y% V.4W% ,%
8)5,*.+343*%.'152/3Q%%
F43*)./0]% M.2*3610]% ?'6I.)610]% j,*1)610]% r.4,+.'0]% ?',5T30.10]% ?+.')% ?1./0]%
H003'6,5%l.50]%P)5Y+3*0]%F2T,*0A%
%
!S%
)01.55)01)8.)%
1W)883*%
P)5,*.--,4)*3%"%
<,03*%,%/.)/)%
/.)/)
P)5,*.--,4)*3%9%
a,',5.--,4)*3b%
42I)%8)5,*.+34*.1)%
42I)
8)5,*.+34*.1)
()4)/.)/)%
T2./,%
:$%
9$%
!"#"$#"!%
<,03*%,%/.)/)%
T2./,%
:"%
<?FHeQ%5213%1)3*3'43]%+)')1*)+,61,]%
1)55.+,4,]%8)5,*.--,4,%
%
%
r3*.N1,*3c%
:9%
9"%
!"#"$#"!%
E1-,,')#
M.01)%*)4,'43%,%03>)*.%8.3'.#O2)6%83*%)>3'3*3%5213%s8250,'437A%
%
r35)1.4t%/.%*)4,-.)'3%*3T)5,I.53%,>*,O3*0)%.5%O,5)*3%/.%O)54,TT.)%
.+8)04,4)%02%,5.+3'4,4)*3%
o*.TT3*%3043*')%83*%
0.'1*)'.--,*3%
57,1X2.0.-.)'3%/35%03T',53%
:!%
H7I-#,-*()%D'2)%6-#
%
o2I)%8)*4,1,+8.)'.]%1,++.')%)=1)%"$%1+]%N'304*3%)=1W3%
::%
99%
!"#"$#"!%
J-*()%..(2-)'%%
+)'4,4)%02%2'%T)'.)+34*)%
P)5,*.--,4)*3%"%Z%,',5.--,4)*3%
:;%
K-2-/%-/-#
%
P3*%*.O35,-.)'3%/35%03T',53u%3`3>)%()4)353>*.1)%
:K%
9!%
!"#"$#"!%
C<6%**-<6-,%-#
P3*+3>3%53>2*,%/35%03T',53%1,>2*,4)%/,5%()4)/.)/)%
B,O)%@jB%/,%()4)0.)/)%
a03T',53b%
B,O)%@jB%/,%1W)883*%%
a4*.TT3*%)%*.(3*.+3'4)b%
:L%
&5%03T',53%,88,*3%1)+3%2'7)'/,%X2,/*,A%&%+,00.+.%1)**.08)'/)')%,%X2,'/)%.5%
1W)883*%5,01.,%8,00,*3%5,%5213]%.%+.'.+.%,%X2,'/)%.5%1W)883*%I5)11,%5,%5213A%
+.02*,%/.`3*3'-.,53%
<213%,+I.3'4,53%Z03T',53%
%$%aFHvj?<Hb%
<.O355)%5213%,+I.3'4,53%
:R%
9:%
!"#"$#"!%
:S%
J)',()(.%-&'#/'**'#<-*7.%-&%#
%
P*38,*,*3%4*3%0)52-.)'.%,%1)'13'4*,-.)'.%/31*3013'6%1)+8*303%4*,%$A$;%3%$A!%
T#+5]%/.523'/)%.'%,1X2,%2'7)88)*42',%X2,'64t%/355)%-211W3*)%8*301354)%
aT521)0.)]%0,11,*)0.)%)%(*2>)0.)b%
%
<,01.,*3%43*+)04,4,*3%,%9;\B%83*%42>,%5,%')>3]%.'%+)/)%/,%*,TT.2'T3*3%
3X2.5.I*.)%4*,%53%()*+3%,')+3*.1W3%
%
%
;$%
9;%
!"#"$#"!%
E-<2)7.%-&'#/'*#<'27,#'#(**%&'(D'&2-#L!M#
%
E.00,*3%,55,%T2./,%2'%1)+8)'3'43%)=1)%,55,%O)54,]%.'%)*/.'3]%,%8,*6*3%/,5%5,03*A%
P*.+,% /.% ,113'/3*3% .5% 5,03*% 0.043+,*3% 2')% 01W3*+)% +.55.+34*,4)% ,55,% N'3% /355,%
T2./,%83*%a.b%.'43*13>,*3%.5%(,01.)%3%a..b%,55.'3,*5)%.'%+)/)%1W3%8*)13/,%52'T)%2',%
4*,.3>)*.,%.5%8.w%8)00.I.53%/*.>,A%
%
?>3'-.)'3Q% P3*% *,T.)'.% /.% 0.12*3--,% .5% (,01.)% 5,03*% /3O3% ,00)524,+3'43% 03+8*3%
3003*3%/.*3>)%.'%+)/)%/,%.'1./3*3%0255)%01W3*+)A%D3'4*3%0.%.'03*.01)')%53%,54*3%
1)+8)'3'6% 083T'3*3% .5% 5,03*% )882*3% 8)**3% /,O,'6% ,/% 300)% 2'% )04,1)5)%
,00)*I3'43Q%1.x%83*%3O.4,*3%*.y300.)'.%.'1)'4*)55,43A%
%
%
;"%
E-<2)7.%-&'#/'*#<'27,#'#(**%&'(D'&2-#L9M#
%
M)8)%.5%5,03*%.'03*.*3]%'3557)*/.'3Q%
G%&5%1W)883*%
G%&5%8*.+)%8)5,*.--,4)*3%
G%&5%031)'/)%8)5,*.--,4)*3%a,O3'/)%12*,%/.%5,01.,*3%4*,%.%/23%2')%08,-.)%,/3T2,4)%
83*%.5%0211300.O)%.'03*.+3'4)%/35%8)*4,1,+8.)'3b%
G%&5%()4)/.)/)%
G%&5%8)*4,1,+8.)'3%a42I)%8)5,*.+34*.1)b%
%
?55.'3,*3% )T'.% 1)+8)'3'43% .'% +)/)% 1W3% .5% (,01.)% ')'% O3'T,% /3O.,4)% a.5% (,01.)%
/3O3%.'1./3*3%03+8*3%0255)%04300)%82'4)%/355)%01W3*+)b%
%
jA@A% 83*% )>3'3*3% 2',% I2)',% *.8*)/21.I.5.4t]% .5% 42I)% 8)5,*.+34*.1)% jlj% /3O3%
3003*3%*.+)00)%)%08)04,4)%X2,'/)%0.%1,+I.,%0)52-.)'3%
%
%
;9%
9K%
!"#"$#"!%
N')%46(#/'**(#*'00'#/%#>(*7<#
%
e.3+8.*3%.5%42I)%8)5,*.+34*.1)%1)'%,1X2,%/3.)'.--,4,A%
%
o*)O,*3% .5% 82'4)% /.% I2.)% a8)5,*.--,4)*3% 3% ,',5.--,4)*3% 0)')% 83*83'/.1)5,*.b]%
1)**.08)'/3'43%,5%+.'.+)%/.%4*,0+.00.)'3%
e2)4,*3% 8*)T*300.O,+3'43% 57,',5.--,4)*3% 3% *3T.04*,*3% 57.'43'0.4t% /35% 03T',53% .'% 2'%
*,'T3%/.%,'T)5.%,II,04,'-,%,+8.)%a9$$G99$\b%3%1)'%2'%1)'T*2)%'2+3*)%/.%82'6%.'%
+)/)%/,%8)43*%O3*.N1,*3%5,%53TT3%/.%D,520A%F.%1)'0.T5.,%/.%*3T.04*,*3%82'6%8.w%N=%.'%
8*)00.+.4t%/3.%+.'.+.%/.%4*,0+.00.)'3%83*%,O3*3%+,TT.)*3%8*31.0.)'3A%
%
e.8343*3%5,%+.02*,%83*%,5+3')%!%O)543%83*%,O3*3%2',%06+,%/35573**)*3%04,6061)A%
%
P5)>,*3% 57.'43'0.4t% /35% 03T',53% .'% (2'-.)'3% /3557,'T)5)% /.% *)4,-.)'3% !% 3% /.% 1)09!% 3%
/.01243*3%T5.%,'/,+3'6%4*)O,6A#
;!%
>%<7)(#/'*#,-2')'#-O6-#)-2(2-)%-#/%#<-*7.%-&%#/%#.7661')%#(#6-&6'&2)(.%-&%#
6)'<6'&5#
#
e.3+8.*3%.5%42I)%1)'%5,%8.w%/.52.4,%/3553%0)52-.)'.%.'%30,+3A%M343*+.',*3%.5%O,5)*3%
,'T)5,*3%/355,%'2)O,%8)0.-.)'3%/.%I2.)]%1W3%0.%0,*t%08)04,4)%,%1,20,%/35%8)43*3%
*)4,4)*.)%/355,%0)52-.)'3A%%
D.02*,*3% 57.'43'0.4t% /35% 03T',53% 83*% 2',% /31.',% /.% 82'6% .'4)*')% ,55,% 8)0.-.)'3% /.%
+.'.+)A%j)4)%.5%O,5)*3%/355)%08)04,+3'4)%,'T)5,*3]%5,%1)'13'4*,-.)'3%3%.5%1,++.')%
)=1)]%1,51)5,*3%.5%8)43*3%)=1)%*)4,4)*.)%0831.N1)A%?>3'-.)'3%,553%2'.4t%/.%+.02*,c%
%
%
"
T
% [! ] ! = CL
%
e.8343*3%,5+3')%!%O)543%83*%1.,012',%/3553%4*3%0)52-.)'.A%
F42/.,*3%57,'/,+3'4)%/35%8)43*3%)=1)%*)4,4)*.)%.'%(2'-.)'3%/355,%1)'13'4*,-.)'3%3%
1)++3'4,*3%57,'/,+3'4)A%
;:%
9L%
!"#"$#"!%
:'2')D%&(.%-&'#/'**(#6-&6'&2)(.%-&'#/%#7&(#<-*7.%-&'#%&6-0&%2(#
%
j)4)%.5%O,5)*3%/35%8)43*3%)=1)%*)4,4)*.)%/355)%-211W3*)%.'%30,+3]%/343*+.',*3%
5,%1)'13'4*,-.)'3%/.%2',%0)52-.)'3%.'1)T'.4,A%
M.01243*3%53%8)00.I.5.%()'6%/.%3**)*3A%
%
%
;;%
>%<7)(#/'*#,-2')'#-O6-#)-2(2-)%-3#7&%2P#/%#D%<7)(#
#
%Q%,'T)5)%/.%12.%0.%z%08)04,4)%.5%82'4)%/.%I2.)]%1)**.08)'/3'43%,55,%*)4,-.)'3%/35%
8.,')%/.%8)5,*.--,-.)'3A%B)**.08)'/3%,%&B@A%j35%')04*)%1,0)%+.02*,4)%.'%T*,/.%
0300,T30.+,5.%a/3Tb%
BQ%1)'13'4*,-.)'3%
<Q1,++.')%)=1)%
%
T
[! ]! =
20
[! ] D
=
"
CL
/.%0)5.4)%308*300)%.'Q%
/3T%/+G"%1+!%TG"%
!
CL
<3TT3%/.%@.)4%
ao^9$\B] "^*.T,%M%/35%0)/.)%,%;RSA!%'+b%
;K%
9R%