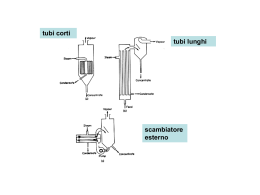
Corso di TRASMISSIONE DEL CALORE
Anno Accademico 2012/2013
‐ Scambiatori di Calore‐
Prof. Ing. Renato RICCI
Dipartimento di Ingegneria Industriale e Scienze Matematiche – Università Politecnica delle Marche
Tipologie di Scambiatori
Concentric Tube Heat Exchangers
g
Parallel Flow
Counterflow
Mixed and Unfinned
Cross Flow Heat Exchangers
Unmixed and finned
Tube-Fin
Compact Heat Exchangers
Compact Heat Exchangers
Plate-Fin
2
Classificazione Scambiatori
Caratteristiche
Costruttive
Compattezza
Tubo in Tubo
A Piastre
Tubi e Mantello
A Piastre Alettate
Tubi Alettati
Rigeneratori
As Area di Scambio su di un Lato

V
Volume
 m2 
As
m2
700 
COMPATTI
 6000  3  (Radiatore Auto  1000 3 )
V
m
 m 
 m2 
As
NONCOMPATTI
70 <
 700  3  (Tubo in Tubo, Tubo ‐ Mantello)
V
 m 
Equicorrente
Situazione Fluidodinamica
Controcorrente
A Flussi Incrociati (Mescolati – Non Mescolati)
Condensatori
Meccanismo di Scambio Termico
3
Evaporatori
Boilers
Radiatori (Applicazioni Spaziali)
Scambiatori a Tubi e Mantello
Gli scambiatori a tubo e mantello sono
reali ati da un guscio esterno,
realizzati
esterno in cui
scorre uno dei dei fluidi, e da un tubo
interno al guscio in cui scorre l’altro fluido.
Si p
possono avere situazioni come q
quelle di
figura a) con un passaggio nel tubo ed uno
nel mantello; oppure situazioni come la b)
con un passaggio nel mantello e due nei
tubi Il doppio passaggio nei tubi fa si che
tubi.
ci siano parti in equicorrente e parti in
controcorrente.
Questa tipologia di scambiatori è
largamente usata per la sua versatilità in
termini di materiali, dimensioni, pressioni
e temperature.
4
Scambiatori a Tubi e Mantello
I Buffles servono a supportare meccanicamente i tubi all’interno del guscio ed allo stesso tempo direzionano
ill fluido
fl d che
h scorre all suo interno in modo
d che
h possa incontrare trasversalmente
l
l tubazioni
le
b
e si venga cosìì
ad uniformare lo scambio termico.
Le due soluzioni rappresentate a sinistra sono particolarmente indicate per incrementare le prestazioni di
scambio termico per una data caduta di pressione ed in un piccolo spazio di ingombro. Le soluzioni riportate
centralmente aiutano invece a contenere le perdite di pressione attraverso la presenza di zone di by‐pass. La
soluzione a destra è invece usata spesso in impianti nucleari, dove una combinazione di flusso longitudinale
e trasversale consente una minore perdita di pressione nel lato guscio.
5
Scambiatori di Calore a Piastre ((PlateHeatExchangers
PlateHeatExchangers))
Negli scambiatori a piastre i due flussi, in genere in controcorrente,
entrano dal lato del coperchio fisso. Le guarnizioni sono disposte in
modo tale che il fluido 1 ed il fluido 2 possano scorrere solo su lati
alterni. Per superare problemi legati a fluidi corrosivi e ad alte
pressioni, gli scambiatori a piastre vengono realizzati anche mediante
saldatura.
ld
6
Tipologie di Scambiatori
Uno scambiatore a lamelle è una forma
semplificata di scambiatore a tubo e mantello
che funzione a singolo passaggio, in
controcorrente con un’estremità fissa e l’altra
mobile per compensare le dilatazioni termiche.
7
Gli scambiatori compatti sono realizzati assemblando
fi i corrugate
t che
h creano condotti
d tti di passaggio
i
superfici
ad elevata superficie di scambio. Le alette vengono
connesse alle superfici per brasatura, saldatura,
incollaggio,
gg , fusione,, interferenza meccanica o
estrusione.
Scambiatori a tubi alettati
Nel caso di scambio termico fra gas e liquido si ha normalmente una marcata differenza del
coefficiente di scambio termico convettivo, con un valore di un ordine più grande per il liquido
rispetto al gas. Per bilanciare lo scambio termico si è soliti alettare sul lato gas così da
aumentare l’area di scambio dove il coefficiente h risulta penalizzato. I tubi possono avere
singole alette oppure possono essere assemblati in modo tale da avere le superfici alettate
comuni a più tubi. Le connessioni possono essere fatte per interferenza meccanica, saldatura,
brasatura, fusione, incollaggio etc.
8
Schemi Base
Nello scambiatore equicorrente i due
fluidi procedono nella medesima
direzione e nello stesso verso. La
limitazione principale di tale sistema sta
nel fatto che la temperatura di uscita del
fluido freddo non potrà mai essere
maggiore della temperatura di uscita del
fluido caldo.
T1  Th,1  Tc,1  Th,in  Tc,in
T2  Th,2  Tc,2  Th,out  Tc,out
Nello scambiatore controcorrente i due
fluidi procedono nella medesima
direzione ma nel verso opposto. In tale
sistema la temperatura di uscita del
fluido freddo potrebbe essere maggiore
della temperatura di uscita del fluido
caldo.
T1  Th,1  Tc,1  Th,in  Tc,out
T2  Th,2  Tc,2  Th,out  Tc,in
9
Tipiche Distribuzioni Assiali di Temperatura
T
T
T
DT2
DT1
L
DT Uniforme
Condensatore
Evaporatore
T
L
Equicorrente
q
10
Controcorrente
Un passaggio nel
mantello e due
passaggi nei tubi
Scambiatore controcorrente
Si prenda il caso di uno scambiatore tubo in tubo controcorrente. Il differente valore della
capacità termica dei due fluidi condiziona gli andamenti di temperatura. Come è possibile
osservare nelle figure a) e c) il fluido avente la minore capacità sarà quello che sperimenterà il
maggiore salto termico fra ingresso ed uscita. Nel caso b) si osserva invece la situazione
particolare in cui le capacità termiche sono uguali e si mantiene di conseguenza il medesimo
delta termico lungo
g tutto lo scambiatore.
11
Metodologia di calcolocalcolo-Approccio Energetico
 ;T
m
 c c,out
 ;T
m
 h h,out
 ;T
m
 h h,in
Fluido Caldo:
 ;T
m
T
 c c,in
Fluido Freddo:
Th  Th,in
h i  Th,out
h t
Tc  Tc,outt  Tc,in
i

 m
 h  hh,in  hh,out
Q
 h


 m
 c  hc,out  hc,in
Q
c
Se il Fluido è Monofase:
Se il Fluido è Monofase:

 m
 h cp,h  Th,in  Th,out
Q
h
Ipotesi: 

 m
 c cp,c  Tc,out  Tc,in
Q
c
 m
 h cp,h  Th
Q
h

 m
 c cp,c  Tc
Q
c
Se il Fluido è in cambiamento di fase:




 h  rh xh,in

Q h  m
h in  x h,out
h out Qc  mc  rc xc,out
c out  xc,in
c in

12


Mantello esterno adiabatico
Processo stazionario

Q h  Q c  Q

Metodologia di calcolocalcolo-Approccio Energetico
 ;T
m
 c c,out
 ;T
m
 h h,out
 ;T
m
 h h,in
 ;T
m
T
 c c,in
T

Q  U  A  T 
R

U:
Coefficiente Globale di Scambio Termico [W /m2 K]
A:
Area Equivalente Totale di Scambio Termico [m
Area
Equivalente Totale di Scambio Termico [m2]
T :
Differenza media di temperatura fra i due fluidi [K]
R=1/UA : Resistenza Termica Totale [K/W]
13
Metodo del Delta T medio Logaritmico Tm,ln
 ;T
m
 c c,out
 ;T
m
 h h,out
 ;T
m
 h h,in
 ;T
m
T
 c c,in
Q  U  A  Tm

Tm,lin
T1  T2

2
Tm,ln
ml
T2  T1

 T2 
ln 

 T1 
Il DTm,ln approssima molto meglio il DTm che effettivamente scaturisce dalla differenza di temperatura dei
due fluidi lungo lo scambiatore. Il DTm,lin tende invece a sovrastimare, pertanto si rischia di
sottodimensionare lo scambiatore.
14
Metodo del Delta T medio Logaritmico Tm,ln
Ipotesi iniziali:
•
Funzionamento stazionario;
Funzionamento stazionario;
•
Calori specifici costanti (assunti come funzione del valor medio di temperatura);
•
Conduzione di calore assiale trascurabile;
•
Superficie esterna isolata
T1  Th,1  Tc,1
T2  Th,2  Tc,2
Tx  Th,x
,  Tc,x
, perunagenericasezionex;
A  p L dA  p dx dove p è il perimetro del tubo.
Il l
Ilcalorecedutodalfluidocaldo
d t d lfl id
ld :
Q  m h  c p ,h  Th  m h  c p ,h  (Th,1  Th,2 ) W  ;
Ilcaloreacquistatodal fluido freddo : Q  m c  c p ,c  Tc  m c  c p ,c  (Tc,2  Tc,1 ) W  ;
inun trattoinfinitesimo :
15
dQ h   m h  c p ,h  dTh W  e dQ c  m c  c p ,c  dTc W 
Metodo del Delta T medio Logaritmico Tm,ln
Ipotesi iniziali:
•
Funzionamento stazionario;
Funzionamento stazionario;
•
Calori specifici costanti (assunti come funzione del valor medio di temperatura);
•
Conduzione di calore assiale trascurabile;
•
Superficie esterna isolata
In un tratto infinitesimo:
dQ h  m h  c p ,h  dTh W  e dQ c  m c  c p ,c  dTc
W 
si osservi che dTh  0;
risolvendo
i l d rispetto
i tt alle
ll diff
differenze di ttemperatura:
t
dQ h
dQ c
dTh  
e dTc 
;
m h  c p, h
m c  c p,c
sottraendo
d membro a membro
b
b :

1
1

dTh  dTc  d (Th  Tc )  dQ  
 m h  c p, h m c  c p,c

16

 poichè dQ h  dQ c


Metodo del Delta T medio Logaritmico Tm,ln
Ipotesi iniziali:
•
Funzionamento stazionario;
•
Calori specifici costanti (assunti come funzione del valor medio di temperatura);
•
Conduzione di calore assiale trascurabile;
Conduzione di calore assiale trascurabile;
•
Superficie esterna isolata

1
1 

dTh  dTc  d(Th  Tc )  dQ  


 m
 h cp,h m
 c cp,c 
poichèdQ  dQ
h
c
lapotenzatermicascambiatainuntrattoinfinitesimoè:
dQ  U (T  T )  dA;
h
c
sostituendo :

1
1 
d(Th  Tc )  U (Th  Tc )  dA  

;
 m
 h cp,h m
 c cp,c 

17
Metodo del Delta T medio Logaritmico Tm,ln
separando le variabili e integrandotra ingresso e uscita dello scambiatore:
T2

T1
A

d(Th  Tc )
1
1 
  U 

  dA;
 m
 h cp,h m
 c cp,c 
(Th  Tc )

0

 T2 
1
1 
l 
ln
UA 


  UA
 m
 h cp,h m
 c cp,c 
 T1 
 h cp,h (Th,1  Th,2 )  Q c  m
 c cp,c (Tc,2  Tc,1 )
Q h  m
quindi:
(T  T )
1
 h,1 h,2
 h cp,h
m
Q
e
(T  T )
1
 c,2 c,1
 c cp,c
m
Q
 (Th,1,  Th,2

 T 
, ) (Tc,2
,  Tc,1
, )
ln  2   UA
UA 


Q
Q
 T1 


 T 
Q  ln  2   UA(T1  T2 )
 T1 
Posto Tm,ln
18


(T2  T1 )
Q  UA 
 T 
ln  2 
 T1 
(T2  T1 )
si ha Q  UA  Tm,ln
 T 
ln  2 
 T1 
Il Coefficiente Globale di Scambio Termico
Rc = resistenza convettiva
Rk = resistenza conduttiva
Rf = resistenza di sporcamento
Rtot= Rc,h
c h + Rf,h
f h + Rk,w
k w + Rf,c
fc
+ Rc,c
UA=1/Rtot
19
Calcolo delle Resistenze
Resistenza Convettiva:
S
Senza
Al tt t
Alettature:
Rc,h 
Con Alettature:
Rc 


1
h A
Rc,c 
h
1
0  h
h A


c

dove 0  efficienza della superficie alettata

1
h A



q  0  hc  A Ts  T  hc  Anon alettata  aletta  N  Aaletta  Ts  T 



 hc  A  N  Aaletta  aletta  N  Aaletta  Ts  T 

 N  Aaletta
 hc  A  1
1 aletta   Ts  T
A


da cui

0  1

20
N  Aaletta
1 aletta
A

 


Calcolo delle Resistenze
UA
1
R f ,h ''
R f ,c ''
1
1

 Rk , w 

0  h  Ah 0  Ah
0  Ac 0  h  Ac
Combinazione di Fluidi
U [W / mq K]
Acqua-Acqua
850 ÷ 1700
Acqua-Olio
110 ÷ 350
Valori Tipici del Fouling Factor
Fluido
Acqua di mare
R’’f x 104
1.75 ÷3.5
Condensatore di Vapore
1000 ÷ 6000
Acqua trattata per caldaie
Condensatore di Ammoniaca
800 ÷ 1400
Acqua di Fiume
3.5 ÷5.3
Condensatore di Alcool
250 ÷ 700
Olio Combustibile
0.9 ÷3.5
25 ÷ 50
Liquidi Refrigeranti
1.75
Scambiatore a tubi alettati
21
0.9
Calcolo delle Resistenze
Resistenza Conduttiva:
s
per parete piana
 A
con s spessore della parete
Rk,w 
D 
ln  0 
 Di 
Rk,w 
per parete cilindrica
2    L
con L lunghezza del tubo
D o diametroesterno
D i diametrointerno
Resistenza delle Incrostazioni:
22
Rf 
R f ''
0  A 
Scambiatori Multipassaggio e a Flusso Incr.
Nel caso di scambiatori a tubo e mantello, sia mono che multi‐passaggio, e di quelli a
flussi
uss incrociati,
c oc at , sebbe
sebbenee lee co
condizioni
d o d
di flusso
usso ssiano
a op
più
ù co
complicate,
p cate, laa d
differenza
ee ad
di
temperatura media logaritmica può essere espressa in termini di quella calcolata in
condizioni controcorrente applicando un opportuno fattore correttivo F (funzione della
geometria e del tipo di scambio).
scambio)
Tm,ln  F  Tm,ln_ CF
con
Tm,ln_ CF 
Th,out  Tc,in   Th,in  Tc,out 
 Th,out  Tc,in 
ln 

 T T
h
,
in
c
,
out


t t
T T
P  2 1 ; R  1 2 1: ingresso; 2 : uscita; T : lato mantello; t : lato tubo
T1  t1
t1  t2
23
Grafici per il Calcolo di F
24
Grafici per il Calcolo di F
25
Esercizio
Lo scambiatore tube‐fins in figura presenta 40 tubi con diametro interno di 5 [mm] e di lunghezza 650 [mm]; i tubi sono legati da alette piane lambite da Aria, mentre all’interno dei tubi scorre Acqua. Il fluido caldo è proprio q
quest’ultima, che entra a 90 [°C] ed esce a 65 [°C], con una portata di 0.6 [kg/s]. Diversamente l’aria entra a 20 [°C] [ ]
[ ]
p
[ g ]
[ ]
ed esce a 40 [°C]. Determinare il Coefficiente Globale di Scambio Termico ,Ui, basato sull’area interna dei tubi.
Ipotesi: 1) Condizioni operative stazionarie
2) i cambi di energia potenziale e cinetica del fluido sono trascurabili, così che la variazione di entalpia totale è dovuta solo alla parte termica
3) Le proprietà del fluido sono costanti. Il calore specifico dell’acqua viene calcolato alla temperatura media fra entrata ed uscita: c p,h  c p,h (77.5)  4195 [J / kg  K ]
 h  c p,h (77.5)  0.6  4195  2517 [J / K ]
Ch  m
Q  Ch  (Th,out  Th,in )  2517  25  62925 [W ]  62.925[kW ]
L’area interna dei tubi è pari a:
Ai    Di  Ni  Li    0.005  40  0.65  0.408[m 2 ]
Q  Ui  Ai  F  Tml ,cf  Ui 
P
t2  t1 65  90

 0.36
T1  t1 20  90
26
Qi
Ai  F  Tml ,c
,cf
R
Tml ,cf 
T1  T2 20  40

 0.80
t 2  t1 65  90
(Th,in  Tc,out )  (Th,out  Tc,in )
T
 Tc,out
l  h,in
ln
T
 h,out  Tc,in
 F  0.97
Ui 



 47.6 [C ]
62925
 3341 [W / m 2K ]
0.408  0.97  47.6
Metodo -NTU
Il metodo del Tml risulta di facile utilizzo nello studio degli scambiatori di calore quando le temperature in
gioco sono note o possono essere determinate da analisi energetiche. Noti infatti il Tml dei due fluidi, le
portate massiche, il coefficiente globale di scambio e la potenza che occorre trasferire, si può determinare la
superficie di scambio mediante:
Q  U  A  Tml
Il metodo del Tml quindi si utilizza essenzialmente per il dimensionamento. I vari step necessari per la
progettazione sono:
• scelta della tipologia di scambiatore adatta alla particolare applicazione;
• determinazione delle temperature incognite in ingresso e in uscita (bilancio energetico);
• calcolo della Tmll e dell
dell’eventuale
eventuale fattore correttivo F;
• scelta o calcolo del coefficiente globale di scambio, U;
• calcolo della superficie di scambio, A.
Qualora non si conoscessero le temperatura di uscita dei due fluidi risulta più indicato un metodo proposto nel
1955 da Kays e da London, chiamato, Effectiveness‐NTU Method. In questo metodo gioca un ruolo
fondamentale
o da e ta e laa Vantaggiosità
a tagg os tà ((Effectiveness)
ect e ess) de
dello
o sca
scambiatore:
b ato e .
27
Metodo -NTU

Potenza Termica Realmente Scambiata
q
q


Massima Potenza Scambiabile
Massima Potenza Scambiabile
qmax Cmin  (Th,in  Tc,in )
La massima potenza scambiabile è ottenibile con uno scambiatore di calore di lunghezza infinita in cui il fluido
con capac
co
capacità
tà te
termica
ca p
più
ù bassa sub
subiràà il massimo
ass o ca
cambiamento
b a e to d
di te
temperatura
pe atu a poss
possibile.
b e.
Tmax  Th,in  Tc,in

Quindi conoscendo  si ricava che:
qmax  Cmin  Tmax

q    Cmin  Th,in  Tc,in  dove Cmin  min m h  c p ,h ; m c  c p,c

Per ogni scambiatore si avrà che:

  f  NTU ,

Cmin
Cmax

UA
 dove NTU è il "Number of Transfer Unit" definito come: NTU 
Cmin

Ad esempio per scambiatore tubo in tubo in e.c:  e.c.
28
 UA  Cmin
1  eexpp  
 1 
C
min
 Cmax


C
1  min
Cmax



Curve -NTU per vari scambiatori
Curve p
per Scambiatore
equicorrente
29
a
flussi
Curve p
per Scambiatore a flussi
controcorrente
Curve -NTU per vari scambiatori
Curve per Scambiatore a tubi e
mantello con un passaggio nel
mantello e più passaggi nei tubi
( lti li di due)
(multipli
d )
30
Curve per Scambiatore a tubi e
mantello
ll
con due
d
passaggii nell
mantello e più passaggi nei tubi
(multipli di quattro)
Curve -NTU per vari scambiatori
Curve p
per Scambiatore a singolo
g
passaggio, flusso incrociato con
entrambi i fluidi non mescolati
31
Curve p
per Scambiatore a singolo
g
passaggio, flusso incrociato con un
fluido non mescolato e l ’ altro
mescolato.
Correlazioni per -NTU
Cr 
32
Cmin
Cmax
Correlazioni per -NTU
33
Metodo -NTU
Le relazioni analitiche sono ovviamente più precise, dato che la lettura del grafico può essere soggetta ad
errori. Relativamente ai grafici per le varie tipologie di scambiatori esistenti vanno fatte le seguenti
osservazioni:
• il valore dell’efficienza (0<<1) aumenta rapidamente per valori di NTU<1.5 e aumenta molto più lentamente
per valori di NTU superiori. Pertanto potrebbe non convenire adottare scambiatori con NTU > 3 ca. (La scelta
i l va condotta
inoltre
d
tenendo
d in
i conto del
d l rapporto benefici/costi).
b
fi i/
i)
• per un dato valore di NTU e del rapporto delle capacità termiche Cr=Cmin/Cmax lo scambiatore in c.c.
presenta e superiore rispetto ad uno scambiatore e.c.
• il rapporto Cr=Cmin/Cmax è tale per cui 0≤Cr≤1:
per un dato valore di NTU
se Cr0
C 0 allora
ll

 max (cambiamento
(
bi
di fase)
f )
se Cr1 allora min
34