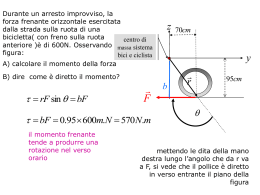
IV Appello di Calcolo delle Probabilità
Laurea Triennale in Matematica 2013/14
17 settembre 2014
Cognome:
Nome:
Email:
Se non è espressamente indicato il contrario, per la soluzione degli esercizi è possibile usare tutti i
risultati visti a lezione (compresi quelli di cui non è stata fornita la dimostrazione).
Esercizio 1. In ciascuna ruota del Lotto vengono estratti uniformemente cinque numeri distinti
(senza reimmissione) nell’insieme {1, 2, . . . , 90}, e le estrazioni su ruote diverse sono indipendenti.
Consideriamo i seguenti eventi:
• A := “il primo numero estratto sulla ruota di Genova, il primo numero estratto sulla ruota
di Milano e il primo numero estratto sulla ruota di Napoli sono quadrati perfetti”,
• B := “i primi tre numeri estratti sulla ruota di Firenze sono quadrati perfetti”,
e indichiamone le probabilità rispettivamente con pA e pB .
(a) Si calcolino pA e pB , mostrando che pA > pB .
(b) Matteo sceglie 3 numeri aleatori con il seguente meccanismo: lancia innanzitutto una moneta
equilibrata; se esce testa, sceglie il primo numero estratto sulla ruota di Genova, il primo
numero estratto sulla ruota di Milano e il primo numero estratto sulla ruota di Napoli; se
invece esce croce, sceglie i primi 3 numeri estratti sulla ruota di Firenze.
Matteo mi comunica che i numeri che ha scelto con tale meccanismo sono tutti quadrati
perfetti. Sulla base di questa informazione, è più probabile che sia uscita testa o croce?
Soluzione 1. (a) Dato che 92 = 81 ≤ 90 mentre 102 = 100 > 90, i quadrati perfetti tra 1 e 90
sono esattamente 9. Nel caso A (estrazioni con reimmissione) si ha
9·9·9
1
pA =
=
= 10−3 ,
90 · 90 · 90
1 000
mentre nel caso B (estrazioni senza reimmissione) si ha
9·8·7
7
pB =
=
< 10−3 = pA .
90 · 89 · 88
9790
(b) Sia T l’evento “esce testa” mentre sia S l’evento “i tre numeri scelti da Matteo sono tutti
quadrati perfetti”. Per ipotesi
1
P(T ) = ,
P(S|T ) = pA ,
P(S|T c ) = pB ,
2
da cui
1
P(S) = P(S|T )P(T ) + P(S|T c )P(T c ) = (pA + pB ) ,
2
quindi la probabilità (condizionale) che sia uscita testa, sapendo che i tre numeri estratti da
Matteo sono tutti quadrati perfetti, vale
P(S|T )P(T )
pA
1
P(T |S) =
=
' 0.59 > ,
P(S)
pA + pB
2
perché pA > pB .
2
Esercizio 2. Siano (Xn )n≥1 variabili aleatorie indipendenti con leggi Exp(1) e definiamo
Sn := X1 + X2 + · · · Xn .
Ricordiamo che che Sn ∼ Gamma(n, 1), ossia Sn è assolutamente continua con densità
fSn (x) =
xn−1 −x
e 1(0,∞) (x) .
(n − 1)!
(a) Tramite un’opportuna integrazione, si mostri che per ogni n ≥ 1 e t ∈ [0, ∞)
tn
+ P(Sn+1 ≤ t) .
P(Sn ≤ t) = e−t
n!
Per t ∈ (0, ∞) fissato, definiamo la variabile aleatoria Nt a valori in N0 ∪ {∞}, ponendo
Nt (ω) := max{n ∈ N : Sn (ω) ≤ t} ,
con le convenzioni max ∅ := 0 e max N := ∞.
(b) Si dimostri la seguente identità, valida per ogni k ∈ N0 e t ∈ (0, ∞):
P(Nt ≥ k) = P(Sk ≤ t).
(c) Si deduca la densità discreta della variabile aleatoria Nt , riconoscendola come nota.
Soluzione 2.
(a) Basta notare che
Z
Z t
t
1
1 t n −x
tn
1
xn−1 e−x dx = xn e−x +
x e dx = e−t + P(Sn+1 ≤ t).
P(Sn ≤ t) =
n!
n! 0
n!
0
0 (n − 1)!
(b) Mostriamo che vale l’uguaglianza di eventi {Sn ≤ t} = {Nt ≥ n}, da cui segue ovviamente
l’uguaglianza delle relative probabilità. Occorre mostrare che
Sn (ω) ≤ t
⇐⇒
Nt (ω) ≥ n .
(1)
Se Nt (ω) ≥ n, essendo Sn crescente in n, si ha
Sn (ω) ≤ SNt (ω) (ω) ≤ t ,
dove l’ultima disuguaglianza segue dalla definizione di Nt . Viceversa, se Sn (ω) ≤ t, allora
n ≤ max{m : Sm (ω) ≤ t} = Nt (ω).
Questo completa la dimostrazione di (1).
(c) Usando quanto mostrato nei punti precedenti
P(Nt = k) = P(Nt ≥ k) − P(Nt ≥ k + 1) = P(Sk ≤ t) − P(Sk+1 ≤ t) = e−t
ossia Nt ha distribuzione Pois(t).
tk
,
k!
3
Esercizio 3. Costruiamo un cubo in R3 , il cui volume X è una variabile aleatoria con densità
1
1(0,8) (x) .
fX (x) =
6 x2/3
(a) Si determini la funzione di ripartizione di X e se ne calcoli il valore medio (se esiste).
(b) Dette Y e Z rispettivamente la superficie di una faccia e la lunghezza di un lato del cubo, si
determini la distribuzione di Y e quella di Z. Le variabili aleatorie Y e Z sono indipendenti?
(c) La distribuzione del vettore (Y, Z) è assolutamente continua?
[Sugg. Si rifletta sul fatto che Y = Z 2 .]
(d) Costruiamo ora tre cubi indipendenti, tutti con la stessa distribuzione del cubo dato, e
indichiamo con W il volume del cubo più grande. Si determini la distribuzione di W .
Soluzione 3. (a) Dato che fX (x) = 0 se x 6∈ (0, 8), q.c. la variabile aleatoria X assume valori in
(0, 8), pertanto FX (x) = P(X ≤ x) = 0 se x ≤ 0 mentre FX (x) = 1 se x ≥ 8. Per x ∈ (0, 8)
possiamo scrivere
Z x
Z x
x1/3
1
dt
=
FX (x) =
fX (t) dt =
.
2/3
2
0
0 6t
In definitiva


se x ≤ 0
0
1/3
x
FX (x) =
se 0 < x < 8 .
2


1
se x ≥ 8
Dato che q.c. X ∈ (0, 8), si ha che E[X] è ben definito e finito, dato da
Z 8
Z 8 1/3
x
84/3
16
E[X] =
x fX (x) dx =
dx =
=
= 2.
6
8
8
0
0
(b) Si ha Y = X 2/3 e Z = X 1/3 , pertanto
FY (y) = P(Y ≤ y) = P(X ≤ y
3/2
) = FX (y
3/2
)=


0
y 1/2
 2

1


0 se
3
3
FZ (z) = P(Z ≤ z) = P(X ≤ z ) = FX (z ) = z2 se


1 se
se y ≤ 0
se 0 < y < 4 ,
se y ≥ 4
z≤0
0<z<2 .
z≥2
Essendo le funzioni di ripartizione C 1 a tratti, sia Y che Z sono variabili aleatorie assolutamente continue, con densità
1
1
fY (y) = FY0 (y) = √ 1(0,4) (y) ,
fZ (z) = FZ0 (z) = 1(0,2) (z) .
4 y
2
Si noti in particolare che Z ha distribuzione uniforme nell’intervallo (0, 2).
Le variabili Y e Z non sono indipendenti, in quanto
P(Y < 1) = P(X < 1) > 0 ,
P(Z > 1) = P(X > 1) > 0 ,
mentre
P(Y < 1, Z > 1) = P(X > 1, X < 1) = 0 .
(c) Il vettore (Y, Z) non ha distribuzione assolutamente continua. Infatti, essendo Y = Z 2 , si ha
P(Y = Z 2 ) = 1, mentre se il vettore (Y, Z) avesse densità potremmo scrivere
Z
Z
Z
2
P(Y = Z ) =
fY,Z (y, z) dy dz =
fY,Z (y, z) dy dz = 0 ,
(y,z)∈R2 : y=z 2
z∈R
y∈R: y=z 2
4
dal momento che, per ogni z ∈ R fissato, il dominio dell’integrale interno consiste di un solo
punto y = z 2 e dunque tale integrale vale zero.
(d) Detti X1 , X2 , X3 i volumi dei tre cubi, si ha W = max{X1 , X2 , X3 }, pertanto
FW (w) = P(W ≤ w) = P(X1 ≤ w, X2 ≤ w, X3 ≤ w) = P(X1 ≤ w)P(X2 ≤ w)P(X3 ≤ w)


se w ≤ 0
0
1/3
= P(X ≤ w)3 = FX (w)3 = ( w 2 )3 = w8 se 0 < w < 8 .


1
se w ≥ 8
Si riconosce la funzione di ripartizione di una variabile uniforme nell’intervallo (0, 8). In
alternativa, essendo la funzione di ripartizione chiaramente C 1 a tratti, segue che la variabile
aleatoria W è assolutamente continua e la sua densità è data da
1
0
fW (w) = FW
(w) = 1(0,8) (w) .
8
5
Esercizio 4. Siano (Xk )k≥1 variabili aleatorie indipendenti e identicamente distribuite, a valori
in {−1, +1}, con la seguente distribuzione:
P(Xk = 1) = p ,
P(Xk = −1) = 1 − p ,
dove p ∈ (0, 1) è un parametro fissato. Definiamo le variabili aleatorie (Yk )k≥1 mediante
Yk := 2Xk ,
quindi definiamo le variabili aleatorie (Zn )n≥0 ponendo
Z0 := 1 ,
Zn :=
n
Y
Pn
Yk = 2
k=1
Xk
.
k=1
(a) Si spieghi perché le variabili aleatorie (Yk )k≥1 sono indipendenti e identicamente distribuite.
Le variabili aleatorie (Zn )n≥1 sono indipendenti e/o identicamente distribuite?
(b) Si mostri che per p < 13 , p = 13 , p >
1
3
si ha rispettivamente E[Yk ] < 1, E[Yk ] = 1, E[Yk ] > 1.
D’ora in avanti fissiamo p = 31 , così che E[Yk ] = 1.
√
√
(c) Si calcoli E[ Yk ], si mostri che E[ Zn ] → 0 e si deduca che Zn → 0 in probabilità.
(d) Si mostri che Zn 6→ 0 in L1 .
(e) La successione Zn ha limite q.c.?
[Sugg.: Si studi il comportamento q.c. della successione
mente la legge dei grandi numeri.]
Pn
k=1
Xk per n → ∞, applicando opportuna-
Soluzione 4. (a) Le variabili aleatorie Yk sono indipendenti e identicamente distribuite, perché
ottenute da variabili aleatorie indipendenti e identicamente distribuite applicando una stessa
funzione misurabile (x 7→ 2x ). Le variabili aleatorie Zk invece non sono né indipendenti né
identicamente distribuite: ad esempio Z1 = Y1 = 2X1 può assumere i valori {2−1 , 21 } = { 12 , 2}
con probabilità rispettive 1 − p e p, dunque ha legge diversa da Z0 ≡ 1; inoltre Z1 e Z2 non
sono indipendenti, dal momento che
P(Z1 = 12 ) = P(Y1 = 21 )?P(X1 = −1) = 1 − p > 0 ,
P(Z2 = 4) = P(Y1 Y2 = 4) = P(Y1 = 2, Y2 = 2) = P(X1 = 1, X2 = 1) = p2 > 0 ,
mentre
P(Z1 = 12 , Z2 = 4) = P(Y1 = 12 , Y1 Y2 = 4) = P(Y1 = 12 , Y2 = 8) ≤ P(Y2 = 8) = 0 .
(b) Si ha
E[Yk ] = E[2Xk ] = 2−1 P(Xk = −1) + 2P(Xk = 1) =
1−p
1 3
+ 2p = + p ,
2
2 2
da cui la tesi segue immediatamente.
(c) Per p =
1
3
si ha
Y
n p n
Y
p
p
E[ Zn ] = E
Yk =
E[ Yk ] ,
√
k=1
k=1
perché le variabili aleatorie Yk sono indipendenti e identicamente distribuite. In particolare
√
√
√
p
p
√ X1
√
1
2
2
2 2
E[ Yk ] = E[ Y1 ] = E[ 2 ] = √ (1 − p) + 2p =
+
=
=: a < 1 ,
3
3
3
2
da cui, essendo a < 1,
n
Y
p
E[ Zn ] =
a = an −−−→ 0 .
k=1
n→∞
6
Per mostrare che Zn → 0 in probabilità basta applicare la disuguaglianza di Markov: per
ogni ε > 0 fissato,
√
p
√
E[ Zn ]
P(|Zn | > ε) = P(Zn > ε) = P( Zn > ε) ≤ √
−−−→ 0 .
n→∞
ε
√
√
√
In√alternativa, si può √notare che E[ Zn ] = k√ Zn kL1 = k Zn − 0kL1 , quindi essendo
E[ Zn ] → 0 segue che Zn → 0 in L1 e dunque Zn → 0 in probabilità. Infine, da ciò segue
facilmente
Zn → 0 in probabilità, dal momento che P(|Zn − 0| > ε) = P(|Zn | >
√ che anche
√
ε) = P( Zn > ε) → 0 per ogni ε > 0.
1
(d) Se si avesseQZn →→ 0 in
QnL , si dovrebbe avere E[Zn ] → 0, ma così non è, dal momento che
n
E[Zn ] = E[ k=1 Yk ] = k=1 E[Yk ] = 1, in quanto E[Yk ] = 1 per un punto precedente.
(e) Sì, si ha Zn → 0 q.c.. Infatti per p = 13 si ha E[Xk ] = −1 23 + 1 13 = − 13 , quindi per la legge
forte dei grandi numeri si ha q.c.
n
1X
1
Xk −−−→ − .
n→∞
n
3
k=1
Di conseguenza, sempre q.c.,
X
n
n
X
1
1
Xk −−−→ ∞ · −
= −∞ ,
Xk = n ·
n→∞
n
3
k=1
da cui segue che q.c.
k=1
Pn
Zn = 2
k=1
Xk
−−−→ 2−∞ = 0 .
n→∞
7
Esercizio 5. Un quotidiano ha l’obiettivo di acquisire almeno 1000 nuovi abbonati. A tal fine,
intende contattare un certo numero di potenziali clienti per offrire loro un mese di prova gratuito.
In base a statistiche precedenti è noto che, dopo un mese di prova, un potenziale cliente ha il 10%
di probabilità di sottoscrivere l’abbonamento.
(a) Usando l’approssimazione normale, si stimi quante persone N è necessario contattare affinché
l’obiettivo di acquisire almeno 1000 nuovi abbonati sia raggiunto col 95% di probabilità.
Un responsabile commerciale suggerisce una strategia alternativa, in cui ai potenziali clienti vengono
offerti tre mesi di prova grauiti, anziché uno. In questo caso, la probabilità che un potenziale cliente
decida di sottoscrivere l’abbonamento, al termine del periodo di prova, diventa del 30%.
(b) Con questa strategia alternativa, quante persone M è necessario contattare affinché l’obiettivo
di acquisire almeno 1000 nuovi abbonati sia raggiunto col 95% di probabilità? Se ogni mese
di prova ha un costo fissato per il quotidiano, quale tra le due strategie è preferibile?
Soluzione 5. (a) Il numero di persone SN che sottoscrivono l’abbonamento ha distribuzione
1
Bin(N, p) con p = 10
. Di conseguenza, per il teorema limite centrale,
1000 − N p
1000 − N p
SN − N p
≥p
'1−Φ p
P(SN ≥ 1000) = P p
N p(1 − p)
N p(1 − p)
N p(1 − p)
N p − 1000
=Φ p
=: Φ(z) ,
N p(1 − p)
dal momento che Φ(−x) = 1−Φ(x) per ogni x ∈ R. Imponendo P(SN ≥ 1000) = Φ(z) = 0.95,
si ottiene z = Φ−1 (0.95). Usando la tavola della distribuzione normale si ha Φ−1 (0.95) ' 1.645,
valore che sostituiremo alla fine. Dunque
p
√
√
N p − 1000
p
= Φ−1 (0.95)
⇐⇒
p( N )2 − p(1 − p)Φ−1 (0.95) N − 1000 = 0 .
N p(1 − p)
√
√
√
Si tratta di una equazione di secondo grado a( N )2 + b N + c = 0 nella variabile N , la
cui soluzione positive è
p
p
√
√
p(1 − p)Φ−1 (0.95) + p(1 − p)Φ−1 (0.95)2 + 4000p
−b + b2 − 4ac
N=
=
.
(2)
2a
2p
Sostituendo p =
1
10
e Φ−1 (0.95) ' 1.645, si ottiene
√
N = 102.50
=⇒
N ' 10 506 .
3
(b) Applicando la formula (2) con p = 10
e Φ−1 (0.95) ' 1.645, si ottiene
√
M = 59.01
=⇒
M ' 3 482 .
Questa strategia richiede M · 3 = 10 446 mesi di prova gratuiti, ed è dunque preferibile a
quella precedente, che ne richiede N = 10 506.
8
Esercizio 6. Sia X = (Xn )n≥0 una catena di Markov con spazio degli stati E := {1, 2, 3, 4, 5}, la
cui matrice di transizione è descritta dal grafo seguente (le probabilità di transizioni da uno stato
in sé stesso i → i sono sottintese):
1
4
1
4
4
3
1
3
5
1
3
2
1
2
1
3
1
(a) Si scriva la matrice di transizione della catena, si determinino le classi di comunicazione e si
classifichino gli stati. Si scrivano quindi le probabilità invarianti.
(b) Se la catena parte inizialmente dallo stato 3, ossia X0 = 3, qual è la probabilità che raggiunga
prima o poi lo stato 5?
[Sugg. Le “probabilità di assorbimento” soddisfano un opportuno sistema lineare.]
Soluzione 6.
(a) La matrice di transizione è data da
2 1

3
3 0 0 0
1 1

 2 2 0 0 0


1
1
1
.
p=
0
0
3
3
3




 0 0 14 21 14 
0
0
0
0
1
Le classi di comunicazione sono R1 := {1, 2}, R2 := {5} (ricorrenti) e T1 := {3, 4} (transitoria).
Ciascuna classe ricorrente, essendo finita, è ricorrente positiva e supporta un’unica probabilità
(2)
(2)
invariante. La probabilità µ(2) supportata da R2 è data semplicemente da µ2 = 1 e µi = 0
(1)
per i 6= 2, mentre la probabilità µ(1) supportata da R(1) è data da µi = 0 per i 6∈ {1, 2},
mentre per i = 1, 2 è soluzione di
(
(
(1)
(1)
(1)
(1)
(1)
(1)
µ1 = µ1 p11 + µ2 p21
µ1 = 23 µ1 + 12 µ2
3 (1)
(1)
⇐⇒
⇐⇒
µ1 = µ2 ,
(1)
(1)
(1)
(1)
1 (1)
1 (1)
2
µ2 = µ1 p12 + µ2 p22
µ2 = 3 µ1 + 2 µ2
(1)
(1)
(1)
(1)
e imponendo che µ1 + µ2 = 1 si ottiene la soluzione µ1 = 35 , µ2 = 25 . In definitiva,
la generica probabilità invariante µ della catena è una combinazione lineare convessa delle
(1)
(1)
probabilità µ1 e µ2 , ossia
µ = αµ(1) + (1 − α)µ(2) ,
con α ∈ [0, 1]. Più esplicitamente,
3
µ1 = α ,
5
2
µ2 = α ,
5
µ3 = µ4 = 0,
µ5 = (1 − α) .
9
(b) Indicando con H {5} := min{n ≥ 0 :
dobbiamo calcolare la probabilità di
probabilità soddisfano il sistema


h1 = 0




h2 = 0

⇐⇒
h3 = p32 h2 + p33 h3 + p34 h4



h4 = p43 h3 + p44 h4 + p45 h5



h = 1
5
da cui h4 =
2
3
e h3 = 31 .
Xn = 5} il tempo di assorbimento nello stato 5,
{5}
assorbimento h3 := h3 := P3 (H {5} < ∞). Tali


h1




h2

h3



h4



h
5
=0
=0
= 13 h3 + 13 h4
= 14 h3 + 12 h4 +
=1
⇐⇒
1
4


h1 = 0




h2 = 0

h3 = 12 h4


3
1


8 h4 = 4


h = 1
5
10
Tavola della distribuzione normale
Rz
− 1 x2
La tabella seguente riporta i valori di Φ(z) := −∞ e√22π dx, la funzione di ripartizione della
distribuzione normale standard N (0, 1), per 0 ≤ z ≤ 3.5. Ricordiamo che I valori di Φ(z) per z < 0
possono essere ricavati grazie alla formula
Φ(z) = 1 − Φ(−z) .
z
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
0.5000
0.5398
0.5793
0.6179
0.6554
0.6915
0.7257
0.7580
0.7881
0.8159
0.8413
0.8643
0.8849
0.9032
0.9192
0.9332
0.9452
0.9554
0.9641
0.9713
0.9772
0.9821
0.9861
0.9893
0.9918
0.9938
0.9953
0.9965
0.9974
0.9981
0.9987
0.9990
0.9993
0.9995
0.9997
0.5040
0.5438
0.5832
0.6217
0.6591
0.6950
0.7291
0.7611
0.7910
0.8186
0.8438
0.8665
0.8869
0.9049
0.9207
0.9345
0.9463
0.9564
0.9649
0.9719
0.9778
0.9826
0.9864
0.9896
0.9920
0.9940
0.9955
0.9966
0.9975
0.9982
0.9987
0.9991
0.9993
0.9995
0.9997
0.5080
0.5478
0.5871
0.6255
0.6628
0.6985
0.7324
0.7642
0.7939
0.8212
0.8461
0.8686
0.8888
0.9066
0.9222
0.9357
0.9474
0.9573
0.9656
0.9726
0.9783
0.9830
0.9868
0.9898
0.9922
0.9941
0.9956
0.9967
0.9976
0.9982
0.9987
0.9991
0.9994
0.9995
0.9997
0.5120
0.5517
0.5910
0.6293
0.6664
0.7019
0.7357
0.7673
0.7967
0.8238
0.8485
0.8708
0.8907
0.9082
0.9236
0.9370
0.9484
0.9582
0.9664
0.9732
0.9788
0.9834
0.9871
0.9901
0.9925
0.9943
0.9957
0.9968
0.9977
0.9983
0.9988
0.9991
0.9994
0.9996
0.9997
0.5160
0.5557
0.5948
0.6331
0.6700
0.7054
0.7389
0.7704
0.7995
0.8264
0.8508
0.8729
0.8925
0.9099
0.9251
0.9382
0.9495
0.9591
0.9671
0.9738
0.9793
0.9838
0.9875
0.9904
0.9927
0.9945
0.9959
0.9969
0.9977
0.9984
0.9988
0.9992
0.9994
0.9996
0.9997
0.5199
0.5596
0.5987
0.6368
0.6736
0.7088
0.7422
0.7734
0.8023
0.8289
0.8531
0.8749
0.8944
0.9115
0.9265
0.9394
0.9505
0.9599
0.9678
0.9744
0.9798
0.9842
0.9878
0.9906
0.9929
0.9946
0.9960
0.9970
0.9978
0.9984
0.9989
0.9992
0.9994
0.9996
0.9997
0.5239
0.5636
0.6026
0.6406
0.6772
0.7123
0.7454
0.7764
0.8051
0.8315
0.8554
0.8770
0.8962
0.9131
0.9279
0.9406
0.9515
0.9608
0.9686
0.9750
0.9803
0.9846
0.9881
0.9909
0.9931
0.9948
0.9961
0.9971
0.9979
0.9985
0.9989
0.9992
0.9994
0.9996
0.9997
0.5279
0.5675
0.6064
0.6443
0.6808
0.7157
0.7486
0.7794
0.8078
0.8340
0.8577
0.8790
0.8980
0.9147
0.9292
0.9418
0.9525
0.9616
0.9693
0.9756
0.9808
0.9850
0.9884
0.9911
0.9932
0.9949
0.9962
0.9972
0.9979
0.9985
0.9989
0.9992
0.9995
0.9996
0.9997
0.5319
0.5714
0.6103
0.6480
0.6844
0.7190
0.7517
0.7823
0.8106
0.8365
0.8599
0.8810
0.8997
0.9162
0.9306
0.9429
0.9535
0.9625
0.9699
0.9761
0.9812
0.9854
0.9887
0.9913
0.9934
0.9951
0.9963
0.9973
0.9980
0.9986
0.9990
0.9993
0.9995
0.9996
0.9997
0.5359
0.5753
0.6141
0.6517
0.6879
0.7224
0.7549
0.7852
0.8133
0.8389
0.8621
0.8830
0.9015
0.9177
0.9319
0.9441
0.9545
0.9633
0.9706
0.9767
0.9817
0.9857
0.9890
0.9916
0.9936
0.9952
0.9964
0.9974
0.9981
0.9986
0.9990
0.9993
0.9995
0.9997
0.9998