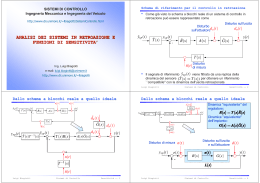
Caratteristiche del controllo
a catena aperta: un esempio
Controllo di velocità di una automobile
• uscita : velocità
• variabile manipolabile : angolo pedale
acceleratore
• disturbo: pendenza della strada
• Incertezze sul modello: peso automobile
Modello autoveicolo (‘semplificato’): v(t)=10α(t)
cioè G(s)=10 (sistema statico, non ha transitorio)
Controllo a catena aperta:
il sistema di controllo non ha informazioni
sull’uscita del processo
Supponiamo di volere seguire un segnale di riferimento vrif(t)=costante=50km/h
Scegliamo per il sistema di controllo una f.d.t C(s)=1/P(s)=1/10
Con tale scelta si ottiene ‘l’inseguimento perfetto del riferimento’
per il sistema nominale
Analizziamo il comportamento del sistema di
controllo a catena aperta in presenza di un
disturbo sull’uscita (ad es. se la strada non è
in pianura si riduce la velocità finale in modo
proporzionale alla pendenza:
-
1
V  50 10  10  50  10
10
non si ha più l’inseguimento perfetto
Analizziamo l’effetto di una variazione
parametrica rispetto al modello nominale:
C(s)=9
1
V  50 9  45
10
non si ha più l’inseguimento perfetto
Consideramo adesso il controllo a catena chiusa, in
cui il sistema di controllo è istante per istante al
corrente dello scostamento tra il riferimento e l’uscita
del processo controllato
supponiamo che la f.d.t. del trasduttore dell’uscita sia
unitaria
10 H ( s )
G( s) 
1  10 H ( s )
Per avere l’inseguimento perfetto deve essere
G(s)=1, cioè H(s)
∞
L’inseguimento perfetto non è possibile
• Scegliamo H(s)=k con k>>, ad esempio
H(s)=1000
1000 * 10
V  50
 Vrif
1  1000 * 10
La bontà dell’inseguimento è proporzionale
al guadagno del controllore
Analizziamo l’effetto del disturbo sull’uscita:
1000 * 10
1
V  50
 10
1  1000 * 10
1  1000 * 10
L’effetto del disturbo è stato attenuato (reiezione dei disturbi sull’uscita)
L’attenuazione del disturbo è proporzionale al guadagno del controllore
Valutiamo l’effetto delle
variazioni parametriche:
V  50
9 * 1000
 50
1  9 * 1000
L’effetto delle variazioni parametriche viene attenuato in modo proporzionale
al guadagno del controllore
Nel controllo a catena chiusa possono essere presenti rumori di misura:
V  50
1000 * 10
10 * 1000
 10
1  1000 * 10
1  1000 * 10
Per attenuare i disturbi di misura il guadagno
del controllore deve essere basso!!!!
Riassunto
Per il controllo in retroazione:
• L’inseguimento migliora al crescere di k
• Si ha una buona attenuazione dei disturbi
sull’uscita, che migliora al crescere di k
• Si ha una buona attenuazione dell’effetto delle
variazioni parametriche, che migliora al
crescere di k
• È possibile che intervengano rumori di misura,
il cui effetto diminuisce al diminuire di k
• Aumenta la complessità di progettazione del
controllore
• Aumentano i costi del sistema di controllo
Schema completo di un sistema di
controllo in retroazione
Trasduttori: misurano le variabili e trasmettono la misura a distanza
es: temperatura tensione
Attuatori: convertono prodotte dal controllore nelle variabili manipolabili
e le amplificano
es: tensione
coppia
Trascuriamo la compensazione del disturbo
Ogni blocco può rappresentare in generale un sistema dinamico nonlineare
tempo variante
Supponiamo che il sistema vari lentamente nel tempo e possa essere
approssimato da un sistema tempoinvariante
Consideriamo il funzionamento del sistema intorno ad un punto di equilibrio
(punto di funzionamento nominale) e supponiamo che le variazioni delle grandezze
siano piccole e che i disturbi siano additivi
Con tali ipotesi ogni blocco è rappresentato da una f.d.t. (sistemi linearizzati)
Usando l’algebra degli schemi a blocchi:
Supponiamo che i due trasduttori siano uguali
Schema di un sistema di controllo in retroazione per piccoli segnali:
La f.d.t del processo include quella dell’attuatore
La f.d.t. del controllore include quella del trasduttore (in genere = K)
Esempio:
controllo di posizione di un montacarichi
Confronto
e f.d.t del
controllore
Attuatore e
processo
Segnale di
riferimento
Sensore di posizione:
potenziometro
(variabile di riferimento)
Uscita:posizione montacarichi
Sensore di posizione:
potenziometro
(variabile di uscita)
Lo scopo è quello di controllare un motore che ha il compito di
sollevare o abbassare un carico, in modo da portarlo ad un’altezza
fissata dall’esterno per mezzo di una levetta
La posizione del carico viene individuata grazie alla presenza della
2° levetta
Le posizioni delle due levette vengono trasdotte, per mezzo di due
potenziometri, in due segnali di tensione
Il sistema di controllo, facendo un confronto tra i due segnali, aziona
il motore per sollevare o abbassare il carico fino a portarlo nella
posizione in corrispondenza della quale si ha e1=e2
E
e1   * r
R
E
e2   * y
R
ρ=resistenza per unità di lunghezza
M=f.d.t. del motore e del montacarichi
Proprietà degli schemi di controllo
Catena aperta
(azione diretta,
open loop control
feedforward control)
Catena chiusa
(controllo in retroazione,
closed loop control
feedback control)
W0  C ( S ) P( S )
C ( S ) P( S )
Wc 
1  C ( S ) P( S ) H ( S )
Condizione di inseguimento
Catena aperta:
C ( S )  P( S )
1
Non è realizzabile! Si approssima inserendo poli a dinamica molto veloce
Catena chiusa:
 C ( S ) P ( S ) H ( S )  1

H (S )  1
Sensitività alle variazioni
parametriche
Definiamo ‘sensitività alle variazioni
parametriche di una f.d.t., dipendente dal
parametro α:

SG 
G
G


G 

 G
• Supponiamo che la f.d.t. del processo da
controllare dipenda da un parametro P ( s,  )
vogliamo calcolare la sensitività del
processo controllato
per il controllo a catena aperta il controllo
non ha effetto sulla sensitività, infatti:

S W0


C (S ) P(S ,  )


C ( S ) P( S ,  )

S W0

C ( S ) P( S ,  )  C (S ) P(S ,  )


P( S ,  ) 

 S P

P( S ,  )
Per il processo controllato a catena chiusa:

SWc




  (1  C ( S ) P( S ) H ( S ))
C ( S ) P( S )
1  C ( S ) P( S ) H ( S ) 
C ( S ) P( S )




C ( S ) P( S )
1  C ( S ) P ( S ) H ( S )  


C ( S ) P(S ) (1  C ( S ) P( S ) H ( S ))  C ( S ) P( S )C ( S ) H ( S ) P(S )
(1  C ( S ) P( S ) H ( S )) 2



SWc 
P ( S )

C ( S )  C ( S ) P( S ) H ( S )  C ( S ) P( S ) H ( S )  (1  C ( S ) P( S ) H ( S ))
2
(1  C ( S ) P( S ) H ( S )) 2
2
C ( S ) P( S )

S
P
SWc 
1  C ( S ) P( S ) H ( S )
La sensitività viene attenuata, si desidera anche in questo caso C (S ) P( S ) H (S )  1
Consideriamo la presenza di disturbi:
Y
CP
1
CPH
r
d
dm
1  CPH
1  CPH
1  CPH
L’attenuazione dei disturbi sull’uscita è garantita da
L’attenuazione dei rumori di misura è garantita da
CPH  1
CPH  1
Definiamo funzione sensitività S(s)
1
S (S ) 
1  CPH
e funzione sensitività complementare
CPH
T (S )  1  S (S ) 
1  CPH
Y ( s )  T ( S ) r ( S )  S ( S )d ( S )  T ( S )d m ( S )
1) T ( S )  1

2) S(S)  0
3) T(S)  0

-  Buon inseguimen to
-  Attenuazio ne disturbo d
-  Attenuazio ne disturbo d m
I disturbi sulla catena diretta e i rumori di misura agiscono in genere
in bande differenti, si cerca quindi di garantire:
Se le bande si sovrappongono si
devono utilizzare schemi di controllo
più complessi (controllo a 2 gdl)
Controllo, supervisione ed automazione
•
Nei sistemi di controllo industriali è spesso presente un controllore di
secondo livello che effettua operazioni di supervisione, con il compito di
elaborare i dati raccolti sulla variabile di controllo e su quella controllata,
aggiornare eventualmente il modello del processo, modificare il controllore
(controllo adattativo) ed effettuare operazioni di diagnostica sul
processo, sul controllore e sulla strumentazione, con il contributo
dell’operatore e tramite opportune interfacce uomo-macchina poste nelle
sale di controllo
•
Un sistema di supervisione si occupa in genere di un gruppo di controllori
ed è a sua volta gestito da controllori di livello superiore
•
Nei sistemi di controllo multilivello in genere i livelli più elevati hanno anche
la funzione di scegliere i riferimenti per i livelli inferiori e comprendono
anche sistemi di controllo sequenziale che controllano la sequenza con
cui vengono svolte determinate operazioni (controllori logici), si parla in tal
caso di sistemi di automazione