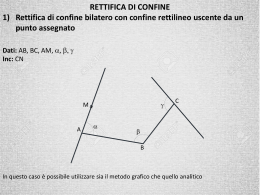
ESERCIZIO GUIDA N.1 (spostamento) Due terreni, uno di forma triangolare ABC e l’altro di forma quadrilatera ABDE confinano tra loro con il lato AB. Si conoscono: AB=21,901m AC=25,440m BC=36,042m Il punto E si trova sul prolungamento del lato CA e il punto D sul prolungamento del lato CB. Si vuole spostare il confine AB in modo che esca da un punto M posto sul lato AE ad una distanza da A di 6,871 m. Calcolare la posizione del punto N secondo estremo del nuovo confine MN. Svolgimento AB 2 AC 2 BC 2 BAC cos 2 AB AC 2 2 2 1 AB BC BC ABC cos 2 AB BC 1 BAE 1 200c BM AM 2 AB 2 2 AM AB cos 1 AB 2 BM 2 AM 2 ABM 1 cos 2 AB BM 1 S ABM AB AM sen1 2 ESERCIZIO GUIDA N.1 (spostamento) MBC 2 1 S ABM S BMN S BMN 1 1 2 BM BN sen 2 2 BN 2 S BMN BM sen 2 Risultati BAC = = 109c,8762 ABC = = 49c,1290 BAE = 1 = 90c,1238 BM = 21,917 m ABM = 1 = 20c,0480 SABM = 74,34 m2 MBC = 2 = 69c,1771 BN = 7,664m ESERCIZIO GUIDA N.2 (spostamento) Due terreni, uno di forma triangolare ABC e l’altro di forma quadrilatera ABDE confinano tra loro con il lato AB. Si conoscono: AB=21,901m AC=25,440m BC=36,042m Il punto E si trova sul prolungamento del lato CA e il punto D sul prolungamento del lato CB. Si vuole spostare il confine AB in modo che risulti perpendicolare al lato AC. Calcolare la posizione degli estremi della dividente MN. Svolgimento AB 2 AC 2 BC 2 BAC cos 2 AB AC 2 2 2 1 AB BC BC ABC cos 2 AB BC 1 BAE 1 200c BK sen1 BK AB sen1 AB AK cos 1 AK AB cos 1 AB AB AK sen1 S ABK 2 ESERCIZIO GUIDA N.2 (spostamento) AB 2 BK 2 AK 2 ABK 1 cos 2 AB BK KBC 2 1 1 S BKMN S ABK MN BK 2 2 S BKMN ( h 1 1 ) c tg100 tg 2 2 S BKMN BK MN AM AK KM h h sen 2 BN BN sen 2 KM h 1 1 2 Risultati BAC = = 109c,8763 ABC = = 49c,1289 BAE = 1 = 90c,1237 AK = 3,384m BK = 21,638m SABK = 36,61m2 ABK = 1 = 9c,8762 KBC = 2 = 59c,0052 MN = 20,328m h = 1,745m AM = 1,639m BN = 2,182m SPOSTAMENTO/RETTIFICA - ESERCIZI ESERCIZIO N.1 Due terreni di forma quadrilatera confinano sul lato AB. del terreno ABCD si conosce: AB = 233,97 m; DAB = = 58c,3063; ABC = = 74c,6613; del terreno ABEF si sa che il punto F si trova sul prolungamento del lato AD dalla parte di A, e che il punto E si trova sul prolungamento del lato CB dalla parte di B. Si vuole spostare il confine AB in modo che esca da un punto noto M posto sul lato AD ad una distanza di 75,04 m da A. Calcolare la posizione del secondo estremo N della dividente. Eseguire la costruzione grafica. [R. BN = 93,48 m] ESERCIZIO N.2 Di due terreni ABCD e CDFE, confinanti sul lato CD, si conoscono le coordinate cartesiane dei vertici: A(50.238 ; 32.579) B(27.823 ; 150.826) C(150.487 ; 182.566) D(133.052 ; 42.537) E(273.151 ; 214.305) F(215.866 ; 52.495) Il confine CD va sostituito con un nuovo confine MN. Sapendo che il punto N si trova sul lato BC a 88,15 m da B, calcolare la posizione del punto M. [R. DM = 38,38 m] SPOSTAMENTO/RETTIFICA - ESERCIZI ESERCIZIO N.3 Due terreni di forma quadrilatera confinano sul lato AB. del terreno ABCD si conosce: AB = 233,97 m; DAB = = 58c,3063; ABC = = 74c,6613; del terreno ABEF si sa che il punto F si trova sul prolungamento del lato AD dalla parte di A, e che il punto E si trova sul prolungamento del lato CB dalla parte di B. Si vuole spostare il confine AB in modo che formi con il lato AD un angolo di 75c. Calcolare la posizione del secondo estremo N della dividente. Eseguire la costruzione grafica. [R. AM = 35,35 m BN = 35,45 m] ESERCIZIO N.4 Di due terreni ABCD e CDFE, confinanti sul lato CD, si conoscono le coordinate cartesiane dei vertici: A(50.238 ; 32.579) B(27.823 ; 150.826) C(150.487 ; 182.566) D(133.052 ; 42.537) E(273.151 ; 214.305) F(215.866 ; 52.495) Il confine CD va sostituito con un nuovo confine MN che risulti perpendicolare al lato BC. Calcolare la posizione della dividente MN. [R. CM = 26,32 DN = 25,87 m] SPOSTAMENTO/RETTIFICA - ESERCIZI ESERCIZIO N.5 Due terreni hanno in comune una spezzata ABC. Un terreno ha forma pentagonale ABCDE mentre i confini dell’altro sono rappresentati in corrispondenza del punto A dal prolungamento del lato AE e in corrispondenza del punto C dal prolungamento del lato CD. Si vuole rettificare il confine ABC in modo che esca da un punto M posto sul lato AE tale che AM = 30 m. Si sono misurati i seguenti elementi: AB = 150,30 m; BC = 122,17 m; EAB = = 88c,8217; ABC = = 131c,0771; BCD = g = 113c,0688; Calcolare la posizione del secondo estremo N della dividente. [R. CN = 114,89 m] ESERCIZIO N.6 I dati dei due terreni sono quelli dell’es. N.5 Sostituire la spezzata ABC con un nuovo confine MN che risulti perpendicolare al lato AE [R. AM = 59,86 CN = 166,96 m] SPOSTAMENTO/RETTIFICA - ESERCIZI ESERCIZIO N.7 Due terreni hanno in comune una spezzata ABC. Un terreno ha forma pentagonale ABCDE mentre i confini dell’altro sono rappresentati in corrispondenza del punto A dal prolungamento del lato AE e in corrispondenza del punto C dal prolungamento del lato CD. Si vuole rettificare il confine ABC in modo che esca da un punto M posto sul lato AE tale che AM = 68 m. Si sono misurati i seguenti elementi: AB = 145,15 m; BC = 154,54 m; EAB = = 53c,5035; ABC = = 245c,7727; BCD = g = 33c,6914; Calcolare la posizione del secondo estremo N della dividente. [R. CN = 19,714 m] ESERCIZIO N.8 I dati dei due terreni sono quelli dell’es. N.7 Sostituire la spezzata ABC con un nuovo confine MN che risulti parallelo al segmento AC. [R. AM = 29,93 m CN = 36,45 m] ESERCIZIO N.9 (rettifica caso 1) Due terreni, contigui hanno in comune la spezzata ABC. Un terreno è ABCDE mentre l’altro si ottiene prolungando i lati EA e DC dalla parte opposta. Si vuole sostituire la spezzata ABC con un nuovo confine rettilineo uscente dal punto M posto sul lato AE con AM=19,277m. Determinare la posizione della nuova dividente. D STAZ. P.B. A E 10c,2015 B 120c,9203 74,627 B C A 38c,2014 ----- 176c,2500 69,769 B 358c,3668 ----- D 73c,5237 ----- g M ----- C [R. CN = 58,99 m] E C.O. (g) DIST. (m) C A B F G ESERCIZIO N.10 (rettifica caso 2)-vedi dati es.1 Due terreni, contigui hanno in comune la spezzata ABC. Un terreno è ABCDE mentre l’altro si ottiene prolungando i lati EA e DC dalla parte opposta. Si vuole sostituire la spezzata ABC con un nuovo confine rettilineo MN (M su AE e N su CD) in modo che l’angolo AMN=e=96c,3974. Determinare la posizione della nuova dividente. STAZ. A B C P.B. D C.O. (g) DIST. (m) E 10c,2015 B 120c,9203 74,627 E Dati: AB, BC, ge ----- A 38c,2014 C 176c,2500 69,769 B 358c,3668 ----- D 73c,5237 ----- e g ---- A B F [R. CN=44,76m AM=8,28m] C G Esercitazione 2 PROVA SCRITTA (mat. Suppl.1986) Gli appezzamenti contigui di due proprietari sono separati da un confine poligonale BCDE e lateralmente sono delimitati dai confini rettilinei coincidenti con gli allineamenti AB ed EF. Partendo dal punto A, sul primo confine rettilineo AB, e terminando nel punto F, sul secondo confine rettilineo EF, si è rilevata la poligonale ABCDEF. Si sono effettuate le seguenti letture: STAZIONE B h = 1,48 m C h = 1,52 m D h = 1,50 m E h = 1,54 m PUNTI COLLIMATI A C B D C E D F ANGOLI (centes.) Azimutale Zenitale 78c,9527 94,3618 237c,1245 -----32c,6407 100c,0000 118c,4365 -----76c,6665 103c,4529 387c,2539 -----126c,6734 100c,0000 195c,7663 100c,0000 Distanze (m) 64,29 -----42,90 -----55,94 -----83,50 125,30 H prisma (m) 1,224 -----2,157 -----1,362 -----1,428 2,210 Graduazione centesimale destrorsa; QA = 75,48 m. Si richiedono: 1. le coordinate e le quote dei vertici della poligonale ABCDEF, assumendo il sistema di riferimento cartesiano con origine nel punto A e l'asse delle ascisse orientato positivamente secondo il lato AB; 2. il disegno del profilo del terreno lungo la poligonale ABCDEF, secondo le opportune scale; 3. dovendosi rettificare il confine poligonale BCDE, si determini, lasciando immutate le aree (di uguale valore unitario) dei due poderi, il nuovo confine rettilineo MN, in modo che risulti parallelo alla congiungente i punti A e F, calcolandone la posizione AM e FN. Esercitazione (mat. Suppl.1986) y Planimetria F Scala 1:1000 2 N e Terreno1 Terreno2 D g A E C B M x 2 12 Esercitazione (mat. Suppl.1986) Argomenti da riguardare per svolgere la prova: - Calcolo dei dislivelli con la livellazione tacheometrica - Calcolo delle quote - Le poligonali aperte - Il problema del trapezio Fasi da seguire per lo svolgimento: - Il profilo longitudinale - Dal libretto di campagna si ricavano gli angoli orizzontali, le distanze ed i dislivelli - Calcolo delle quote dei vertici B, C, D, E, F - Calcolo degli azimut - Calcolo delle coordinate parziali e totali - Calcolo delle distanze AF e BF - Calcolo degli angoli = BAF (con Carnot) e = EFA y Planimetria F - Calcolo della superficie SABCDEFA - Applicazione del problema del trapezio e calcolo dei lati AM e FN N - Disegno del profilo del terreno E e Scala 1:1000 Terreno1 Terreno2 D g A C B M x 2 2 12
Scaricare