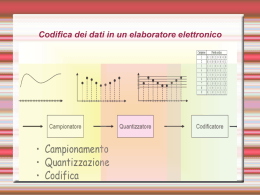
Gianfranco Bentivoglio
INFORMATICA
CAP. 2
LA CODIFICA BINARIA DEI DATI
DISPENSE AD USO DEGLI STUDENTI DEL CORSO DI
“GESTIONE INFORMATICA DEI DATI AZIENDALI”
NOME FILE
AGG. AL:
C AP . 2-C ODIFICA BINARIA R EV . 3 AA05-06. DOC
11/12/05
TOTALE PAGINE
108
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.2
INDICE
ARGOMENTI TRATTATI __________________________________________________6
LA CODIFICA DELL’INFORMAZIONE _______________________________________8
RAPPRESENTAZIONE ANALOGICA/ DIGITALE DELL'INFORMAZ. __________________________________10
ILPROCESSO DI “DECODIFICA” DEI DATI ______________________________________________________12
APPROFONDIMENTO: IL PROCESSO DI CODIFICA _____________________________________________13
IL CONCETTO DI INFORMAZIONE E DATO: UN ESEMPIO_________________________________________16
I DATI SONO UNA SEMPLIFICAZIONE DELLA REALTÀ ___________________________________________18
NON TUTTE LE INFORMAZIONI SONO CODIFICABILI ____________________________________________20
I DATI, DI PER SÉ, SONO PRIVI DI SIGNIFICATO ________________________________________________22
DATI DIVERSI POSSONO RAPPRESENTARE LA STESSA INFORMAZIONE __________________________24
CONVERGENZA DIGITALE __________________________________________________________________26
MOTIVAZIONE TECNOLOGICA PER L’USO DELLA CODIFICA BINARIA ______________________________28
IL BIT ____________________________________________________________________________________30
IL BYTE __________________________________________________________________________________32
CODIFICA DEL SUONO _________________________________________________94
STANDARD DI CODIFICA DEL SUONO_________________________________________________________96
LA CODIFICA STANDARD DI WINDOWS: .WAV __________________________________________________97
UN FORMATO COMPRESSO: MP3 ____________________________________________________________97
IL FORMATO REAL AUDIO___________________________________________________________________98
IL FORMATO MIDI __________________________________________________________________________98
CONFRONTO TRA LE DIVERSE CODIFICHE ___________________________________________________100
MA ALLORA COSA RAPPRESENTA QUEL BYTE IN MEMORIA? ___________________________________102
APPENDICE 1 GLI OPERATORI LOGICI___________________________________104
ESPRESSIONI BOOLEANE _________________________________________________________________106
LE PROPOSIZIONI ________________________________________________________________________108
I SISTEMI DI NUMERAZIONE_____________________________________________34
SISTEMI DI NUMERAZIONE ADDITIVI__________________________________________________________34
SISTEMA DI NUMERAZIONE POSIZIONALE ____________________________________________________36
QUALE È IL NUMERO PIÙ GRANDE CHE SI PUÒ RAPPRESENTARE, NELLA BASE X, CON N CIFRE _____38
LE DIVERSE BASI __________________________________________________________________________40
PASSAGGIO DA BASE “X” A BASE 10__________________________________________________________42
PASSAGGIO DA BASE 10 A BASE “X”__________________________________________________________44
IL VALORE DI UN NUMERO A SECONDA DELLA BASE ___________________________________________46
OPERAZIONI IN BINARIO____________________________________________________________________48
LA MOLTIPLICAZIONE ______________________________________________________________________50
LA CODIFICA BINARIA DELL’INFORMAZIONE ______________________________54
LA CODIFICA DEI CARATTERI _______________________________________________________________56
GLI STANDARD PER CODIFICARE I CARATTERI ________________________________________________58
CODIFICA DEI NUMERI IN ASCII ______________________________________________________________60
CODIFICA DEI NUMERI NATURALI ____________________________________________________________62
CODIFICA DEI NUMERI INTERI _______________________________________________________________64
I NUMERI NEGATIVI CODIFICATI IN COMPLEMENTO A 2 _________________________________________66
CODIFICA BINARIA VS. CODIFICA ASCII _______________________________________________________68
UN COMPROMESSO: LA CODIFICA BCD (BINARY CODE DECIMAL) ________________________________70
BCD VS. BINARIO _________________________________________________________________________72
COME SI PUÒ RAPPRESENTARE UN NUMERO INTERO ? ________________________________________74
NUMERI REALI: LA NOTAZIONE ESPONENZIALE________________________________________________76
NUMERI REALI: LA CODIFICA ________________________________________________________________78
CODIFICA DELLE IMMAGINI _____________________________________________80
UN PRIMO ELEMENTO: LA ”RISOLUZIONE” ____________________________________________________82
UN SECONDO ELEMENTO: LA PROFONDITÀ COLORE___________________________________________83
RIASSUMENDO____________________________________________________________________________84
LE TECNOLOGIE DIGITALI NELL'USO PROFESSIONALE _________________________________________84
FORMATO DELLA CODIFICA GRAFICA (“RASTER”) ______________________________________________86
CODIFICA VETTORIALE_____________________________________________________________________90
I FORMATI VETTORIALI _____________________________________________________________________91
CONFRONTO RASTER – VETTORIALE ________________________________________________________92
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.4
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
PARLEREMO DI...
IL MEZZO SU CUI
RAPPRESENTARE
ED ELABORARE
L’INFORMAZIONE
IL MODO CON
CUI
RAPPRESENTARE
L’INFORMAZIONE
LA MODALITÀ CON
CUI ELABORARE
L’INFORMAZIONE
ARGOMENTI TRATTATI
In questo secondo capitolo parleremo del "modo" con cui si rappresentano le informazioni, affinché possano essere poi trattate con
procedimenti automatici su un computer. Più precisamente verranno trattati i seguenti argomenti:
1. i concetti di "informazione" e "dato", mettendo in evidenza:
• la differenza tra i due termini che, se nel linguaggio corrente vengono usati come sinonimi (con l’accezione di
“conoscenza”, relativa a qualcosa o qualcuno), in ambito strettamente informatico assumono significati profondamente distinti;
• la necessità di codificare l’informazione in modo che
possa essere comunicata e elaborata;
• alcuni aspetti significativi del processo di codifica;
• le motivazioni tecnologiche che, all’interno
dell’elaboratore, rendono necessaria un particolare tipo
di codifica, la codifica binaria;
2. il sistema di numerazione binario, analizzato sotto il punto di vista
prettamente matematico, e visto come un sistema di numerazione alternativo al sistema decimale;
3. la rappresentazione, in formato binario, delle diverse tipologie di
informazione usate dall'uomo (come numeri, testo, suoni, immagini).
• I CONCETTI DI INFORMAZIONE E DATO
• I SISTEMI DI NUMERAZIONE
Infine ci sembra giusto sottolineare l’importanza che gli studi sulla
rappresentazione dell’informazione hanno avuto ai fini di una corretta
comprensione del processo elaborativo messo in atto dal nostro cervello ed il rilevante contributo che, in questo senso, ha dato
l’informatica.
• LA CODIFICA BINARIA
DELL’INFORMAZIONE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.6
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
“CODIFICA”
PER POTER
COMUNICARE ED ELABORARE LE
INFORMAZIONI
SIA DA PARTE DELL’UOMO CHE DI
LA CODIFICA DELL’INFORMAZIONE
Come già detto nell'introduzione,
“L’INFORMAZIONE è la “conoscenza” relativa a oggetti, fatti, concetti, eventi e procedimenti che, in un
certo contesto, ha un particolare significato”
DEFINIZIONE ISO
SISTEMI AUTOMATICI È NECESSARIO
CODIFICARLE
SU UN SUPPORTO FISICO,
MEDIANTE SIMBOLI E OPPORTUNE
REGOLE DI CODIFICA
I DATI RAPPRESENTANO IL
RISULTATO DI QUESTO PROCESSO DI
CODIFICA DELLE
Noi uomini, attraverso i sensi, riceviamo continuamente informazioni dai
nostri simili e dal mondo circostante. Questo processo, che chiamiamo percezione, è tuttavia un fatto immediato, che non ci permette di memorizzare
e di trasmettere ad altri le informazioni che abbiamo percepito.
Il primo problema che dobbiamo affrontare, per poter:
descrivere un fenomeno che non possiamo riprodurre direttamente o
rappresentare un oggetto che non abbiamo a portata di mano;
esprimere un concetto astratto;
comunicare a qualcun’altro la nostra conoscenza;
memorizzare da qualche parte l'informazione che abbiamo percepito
per poterla utilizzare in un secondo momento;
produrre nuove informazioni sulla base di quelle che abbiamo già
acquisito;
è quello di individuare una forma con cui rappresentare le informazioni
affinché queste possano essere comunicate (sia tra uomini, che
tra l’uomo ed una macchina), memorizzate (in modo da essere mantenute
nel tempo) ed elaborate (sia dall’uomo che mediante procedimenti automatici).
INFORMAZIONI
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.8
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
Più precisamente si può affermare che,
affinché una INFORMAZIONE possa essere comunicata, memorizzata ed elaborata, deve essere rappresentata su un supporto fisico, mediante un insieme opportuno di simboli e secondo specifiche regole di codifica.
E questo è sempre vero, sia che il trattamento dell'informazione sia fatto
dall'uomo, che tramite sistemi automatici.
Il risultato finale di questo processo di codifica
dell’informazione è rappresentato dai DATI .
In questo senso si può precisare che:
I DATI sono la rappresentazione delle informazioni in
un determinato codice.
I DATI sono “registrati” su un supporto fisico.
I DATI sono gli “oggetti” che vengono scambiati nel
processo comunicativo.
I DATI sono gli “oggetti” su cui operano i metodi di
elaborazione automatici.
È importante sottolineare che il DATO rappresenta il modo con cui riproduciamo gli aspetti significativi della realtà (ovvero gli aspetti che abbiano
per noi una qualunque rilevanza), indipendentemente dal fatto che poi
quel dato debba essere elaborato o meno con un calcolatore.
Ad esempio:
PER RAPPRESENTARE
UNA PERSONA
UN LUOGO
UN OGGETTO
UN AZIENDA
POTREMMO UTILIZZARE I SEGUENTI DATI
•
•
•
•
•
•
•
•
•
dati anagrafici,
curriculum professionale,
aspetto fisico
dati geografici
dati storici
dati di fabbricazione
dati di utilizzo
ragione sociale,
dati di bilancio
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
La rappresentazione di un'informazione attraverso dei dati è infatti l'unico modo che abbiamo per comunicare, memorizzare ed elaborare l'informazione stessa. Questo processo di codifica dell'informazione assume una rilevanza ancora maggiore quando il trattamento dell'informazione dovrà essere fatto su sistemi automatici.
RAPPRESENTAZIONE ANALOGICA/ DIGITALE DELL'INFORMAZ.
Su un piano fisico la rappresentazione dell'informazione può assumere
due forme:
ANALOGICA: in cui l'informazione è rappresentata in modo
continuo da un'altra grandezza
DIGITALE: in cui l'informazione è rappresentata in modo discreto da una sequenza di campioni (di norma interpretabili
come numeri)
Ad esempio, l'informazione “tempo” può avere una rappresentazione
(o continua) come quella fornita dalla posizione della lancetta
che si sposta sul quadrante dell'orologio oppure una rappresentazione
DIGITALE, attraverso numeri mostrati sul display di un orologio digitale.
ANALOGICA
Allo stesso modo l'informazione “temperatura”, può essere rappresentata attraverso l'altezza della colonnina di mercurio del normale termometro (e quest'altezza varia in modo continuo col variare della temperatura)
oppure attraverso i numeri di un termometro digitale (e la temperatura
indicata varia in modo discontinuo).
Oppure l'informazione “peso” può essere rappresentata, su una bilancia
“analogica” attraverso il movimento dell’ago sul quadrante, mentre una
bilancia digitale mostra il peso attraverso i numeri del suo display. In
questo ultimo caso è importante sottolineare che se la bilancia ha la
precisione di una cifra decimale, potrà mostrare le differenze fra 60,1 e
60,2 grammi, ma non un peso intermedio: infatti le cifre sul display passeranno da 60,1 a 60,2 senza poterlo rappresentare.
Digitalizzazione
Il “mondo reale” è continuo, e mentre la rappresentazione della realtà,
che viene fatta dall'uomo è molto spesso di tipo analogico, quella che
viene usata all'interno del calcolatore, può essere solamente digitale. Il
processo di conversione di grandezze analogiche in grandezze discrete
(digitali) è chiamato “DIGITALIZZAZIONE”. L'uso di segnali discreti
permette la rappresentazione di dati quali testo, immagini, suoni, video,
ecc. tramite numeri binari.
PAG. 2.10
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
“DECODIFICA”
CONOSCENDO IL SIGNIFICATO DEI
SIMBOLI E LE REGOLE DI CODIFICA
È POSSIBILE
ESTRARRE
LE INFORMAZIONI CONTENUTE
NEI DATI ATTRAVERSO UN
PROCESSO DI DECODIFICA
LE INFORMAZIONI SONO IL
SIGNIFICATO CHE NOI
ATTRIBUIAMO AI DATI IN
ILPROCESSO DI “DECODIFICA” DEI DATI
Viceversa, avendo disponibili dei DATI e conoscendo:
• il significato dei simboli con cui sono stati rappresentati,
• e le regole di codifica,
possiamo “estrarre” informazioni dai dati attraverso
un processo di decodifica.
Ad esempio, conoscendo il curriculum di una persona, possiamo
avere un'idea delle sue capacità professionali e decide per se assumerla o meno. Oppure, conoscendo i dati di bilancio di un'azienda, e sapendo interpretare questi dati (le regole di decodifica), possiamo dare un giudizio sull'azienda stessa e decidere se acquistare
azioni o meno.
In altre parole si può affermare che:
premesso che sia nota la conoscenza dei simboli e del
sistema di codifica, la “decodifica” dei DATI “produce”
INFORMAZIONE;
in questo senso l’INFORMAZIONE rappresenta il significato che noi attribuiamo ai DATI in relazione alla realtà
che essi rappresentano.
Un'ultima considerazione che possiamo fare sul processo di codifica dell'informazione è questa:
se è vero che l'uomo comunica attraverso i DATI, allora
è anche vero che, per COMUNICARE, l'uomo ha necessità
di condividere i sistemi di codifica (in base ai quali i
dati stessi vengono prodotti a partire dall'informazione).
RELAZIONE ALLA REALTÀ CHE
ESSI RAPPRESENTANO
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.12
INFORMATICA
APPROFONDIMENTO: IL PROCESSO DI CODIFICA
Dedichiamo al processo di codifica un rapido approfondimento.
Un codice può essere definito dai seguenti tre elementi:
• un alfabeto, ovvero l’insieme dei “segni” elementari
(simboli) che comporranno il codice e mediante i quali
verranno rappresentate le informazioni;
• le regole sintattiche, ovvero l’insieme delle regole che
descrivono come comporre e riconoscere un insieme
corretto e valido di segni;
• le regole semantiche, che indicano come assegnare e
ricavare un significato dai segni.
Definito che sia il codice “X”, definiamo
CODIFICA DI UN’INFORMAZIONE NEL CODICE
“X”
il processo che, utilizzando il codice “X” , porta alla registrazione dell’informazione utilizzando i simboli del suo
alfabeto, composti secondo le regole sintattiche.
Per contro con il termine di:
DECODIFICA DI UN DATO, IN BASE AL CODICE
“X”
indichiamo l’operazione inversa, ovvero quella che in
base alle regole semantiche del codice X permette
l’interpretazione del dato registrato e la ”estrazione”
dell’informazione contenuta.
CAP. 2 - LA CODIFICA BINARIA DEI DATI
Senza volerci addentrare nei meandri della semiologia, ci sembra
interessante evidenziare una importante classificazione dei codici
(G.R.Cardona) nelle seguenti due categorie1:
• Codici elementari, in cui ogni segno dell’alfabeto codifica
direttamente una informazione; essi sono indipendenti dalla
lingua degli interlocutori che debbono leggerli e permettono
di esprimere direttamente un significato. Ad esempio Rientrano in questa prima categoria:
− i cartelli relativi alla segnaletica stradale,
− i simboli utilizzati sui comandi delle auto,
− nel settore informatico appartengono a questa categoria le
icone utilizzate nelle interfacce grafiche dei recenti sistemi.
• Codici strutturati, composti da più segni dell’alfabeto, uniti
secondo regole sintattiche, a volte anche complesse, spesso strettamente dipendenti dalla lingua degli interlocutori.
In questa seconda categoria entrano i sistemi di scrittura (esempio di codifica finalizzato alla comunicazione di informazioni) e numerazione (esempio di codifica di informazioni
quantitative) .Alcuni esempi di codici, che rientrano nelle definizioni appena date, sono i seguenti:
− le note musicali,
− il sistema di misurazione del tempo,
− codici scientifici (chimica),
− codici per telecomunicazioni (protocolli),
− codici crittografici (“codici segreti”).
1 questi concetti saranno utili quando si affronterà lo studio dei codici usati
nell’informatica per la rappresentazione linguistica e numerica
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.14
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
INFORMAZIONE DATO
INFORMAZIONE
IL CONCETTO DI INFORMAZIONE E DATO: UN ESEMPIO
> Quante mele ci sono nella figura ?
> 12
Sicuramente questa sarà stata la risposta di ognuno di noi
In un attimo, senza avere una chiara consapevolezza del complesso processo che stiamo mettendo in atto, abbiamo realizzato un
processo di codifica di una informazione quantitativa mediante:
le cifre decimali (i simboli),
il sistema di numerazione decimale (regole di codifica)
Il risultato di questo processo di codifica è stato il numero 12 (dato);
tale dato successivamente potrà essere comunicato e potrà essere
elaborato.
Anche se avremo modo di approfondire questo concetto nelle pagine che seguono, ci sembra fin da ora importante sottolineare come
12, il dato in quanto tale, non abbia alcun significato se non in relazione alla situazione che abbiamo descritto.
Nei paragrafi seguenti vogliamo approfondire alcuni aspetti del processo di codifica e della differenza che esiste tra informazione e dato:
12
1. IL DATO RAPPRESENTA SOLO UNA PARTE DEL MONDO REALE, QUELLA CHE
CI INTERESSA COMUNICARE, MEMORIZZARE ED ELABORARE ED IN QUESTO
SENSO È UNA SEMPLIFICAZIONE DELLA REALTÀ;
2. NON TUTTE LE INFORMAZIONI SONO CODIFICABILI;
3. I DATI, DI PER SÉ, SONO PRIVI DI SIGNIFICATO; MA I DATI POSSONO ESSERE
ELABORATI ANCHE SENZA CONOSCERE L’INFORMAZIONE CHE
RAPPRESENTANO;
4. DATI DIVERSI POSSONO RAPPRESENTARE LA STESSA INFORMAZIONE E DATI
UGUALI POSSONO RAPPRESENTARE INFORMAZIONI DIVERSE.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.16
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
1° - I DATI RAPPRESENTANO LA REALTÀ ?
I DATI SONO UNA SEMPLIFICAZIONE DELLA REALTÀ
In relazione al processo di codifica delle informazioni, il primo aspetto che è importante sottolineare, è il seguente:
i DATI, in quanto rappresentazione simbolica di informazioni, sono una astrazione di una sola parte del
mondo reale (ovvero di quella parte che si ritiene essere interessante comunicare, memorizzare, elaborare ).
Questo implica che i dati, in quanto astrazione di una parte del
mondo reale, sono anche una semplificazione dei fatti, nel senso
che certe proprietà e caratteristiche degli oggetti reali vengono ignorate in quanto ritenute marginali ed irrilevanti per il particolare utilizzo che se ne intende fare.
QUALI DATI RAPPRESENTANO
AL MEGLIO QUESTA DONNA ?
• ALTEZZA
• COLORE OCCHI
• COLORE CAPELLI
• MISURA SENO
• MISURA VITA
• MISURA FIANCHI
MISS
• TITOLO
STUDIO
• ETA’
• LINGUE
CONOSCIUTE
• STATO CIVILE
• ESPERIENZE
LAVORATIVE
• INDIRIZZO
• ATTIVITÀ
• N. FIGLI
LAVORATRICE CONSUMATRICE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Vedremo nei capitoli successivi come questo aspetto, in fase di
progettazione di un nuovo programma, presenti notevoli criticità per
il fatto che qualcuno debba decidere fino a che punto fermarsi nel
processo di semplificazione, ossia, in altre parole, deve decidere
cosa è importante e cosa non lo è.
Esempio:
Le informazioni relative ad una persona possono essere rappresentati attraverso diverse serie di dati, a secondo delle esigenze di elaborazione
che si possono avere:
• dati relativi all’aspetto fisico (altezza, colore degli occhi, colore dei
capelli, misura del seno,...), se l’obiettivo è la ricerca di una miss;
• dati professionali (titolo di studio, lingue conosciute, precedenti esperienze lavorative), se l’obiettivo è quello di selezionare un nuovo dipendente;
• dati anagrafici (età, attività, stato civile, n. figli, indirizzo di residenza)
se l’obiettivo è quello di identificare un soggetto per realizzare
un’analisi di mercato.
PAG. 2.18
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
2° - TUTTE LE INFORMAZIONI SONO CODIFICABILI ?
NON TUTTE LE INFORMAZIONI SONO CODIFICABILI
Un secondo aspetto su cui vogliamo soffermare la nostra attenzione
è legato alla seguente domanda:
> E’ possibile codificare qualunque informazione?
La risposta è :
> No!
Esistono infatti numerose situazioni in cui noi produciamo nuove informazioni senza passare (almeno in maniera esplicita) attraverso
questo processo di codifica dell’informazione: è il caso delle informazioni afferenti alla sfera emotiva e sentimentale.
L’esempio riportato nella pagina accanto mostra come non sia possibile identificare l’elaborazione eseguita, pur sapendo che la risposta alla domanda “mi piace questo fiore?” , dipenderà dalle tante
informazioni che abbiamo sul fiore (“ha dei bei colori?”, “è profumato?”, “ha un bell’aspetto?”, ecc.).
INFORMAZIONI
DI PARTENZA
A) COLORE
B) PROFUMO
C) ASPETTO
D) ????????
ELABORAZIONE
?
INFORMAZIONE
FINALE
IL FIORE
E’ BELLO (O NON E’ BELLO) !!
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Il fatto di non saper codificare tali informazioni, ci impedisce di decifrare il tipo di elaborazione eseguita dal nostro cervello e quindi, in
definitiva, di riprodurla su delle macchine.
Pertanto questo tipo di elaborazioni non sono riconducibili (almeno
ora e speriamo mai!), negli schemi che andremo a studiare.
PAG. 2.20
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
I DATI, DI PER SÉ, SONO PRIVI DI SIGNIFICATO
3° - I DATI HANNO SIGNIFICATO ?
Una terza considerazione da fare è che:
i dati, in quanto simboli risultanti da un opportuno
processo di codifica, non hanno di per sé alcun significato, ma acquisiscono significato soltanto quando
vengono interpretati da chi ne conosce la chiave di
decodifica e sa come metterli in relazione alla realtà
che essi rappresentano.
50
50
Uno stesso dato, ad esempio “50”, può rappresentare la codifica di
informazioni completamente diverse:
• il voto di un studente che ha sostenuto l’esame di maturità
• il limite di velocità di una strada
• il codice di un prodotto
• Il peso di una valigia
• gli anni di una persona
50
e tanti altri significati ancora. Il dato 50 diventa informazione solamente per chi ne possiede la chiave di decodifica: soltanto di questo modo è possibile attribuire un significato al dato stesso.
Ad esempio, noi possiamo capire il significato che può avere il dato
50, inteso come voto, solamente se conosciamo il sistema di codifica decimale e se abbiano chiaro il concetto di “esame” e di “voto”
associato all'esame stesso.
50
50
NO, MA COMUNQUE
POSSONO ESSERE ELABORATI
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Ma i dati, benché privi di un loro proprio significato,
possono comunque essere elaborati: basta conoscere le regole in base alle quali vanno manipolati.
Questo è quello che succede all'interno del computer: per elaborare
i dati non è necessario conoscerne il significato, ma è sufficiente
avere un programma che “sappia” come devono essere “manipolati”
per produrre il risultato atteso.
E Il risultato dell'elaborazione, anch’esso un dato, potrà poi essere
utilizzato da chi, possedendo le regole di decodifica, sarà in grado
di “interpretarlo”.
PAG. 2.22
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
4° - DATI DIVERSI = STESSA INFORMAZIONE ?
IL RISULTATO DI UN ESAME
PUÒ ESSERE ESPRESSO IN:
• VOTO DA 1 A 30
• VOTO DA 1 A 10
• VOTO DA 1 A 60
• GIUDIZIO: IDONEO,
NON IDONEO
IL FATTURATO DI UNA AZIENDA
SI PUÒ INDICARE:
ANNO 2003 € 150 MIL.
ANNO 2004 € 160 MIL.
ANNO 2005 € 195 MIL.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
DATI DIVERSI POSSONO RAPPRESENTARE LA STESSA
INFORMAZIONE
Un ultimo aspetto (che può sembrare ovvio ma è importante capire
bene) è che non esiste un solo modo per codificare una informazione, ma che anzi spesso esistono diversi modi, tra loro equivalenti,
di codificare la stessa informazione.
La scelta di una forma di codifica, piuttosto che un’altra, è spesso
un fatto puramente convenzionale ed è legata alla:
chiarezza e alla facilità di utilizzo da parte di chi la dovrà
usare;
definizione di standard comuni, che ne semplificano la comunicazione.
Come logica conseguenza, se dati diversi possono rappresentare la
stessa informazione (30, 10, 60 rappresentano il voto massimo) è
anche vero che dati uguali possono rappresentare informazioni diverse (si consideri il diverso significato che può avere un voto uguale a 10).
Di norma, sarà possibile realizzare delle:
“funzioni di trasformazione”
da una forma di codifica all’altra. Ma poiché i dati sono anche una
“semplificazione” della realtà, non è detto che due diverse forme di
codifica siano sempre equivalenti, per tutti i particolari del mondo
reale che vogliono rappresentare. Se questo succede, potrebbe essere possibile la trasformazione dalla codifica “X” alla codifica “Y”
ma non viceversa.
Come esempio prendiamo il sistema di numerazione utilizzato da alcune tribù primitive, basato su tre simboli (1, 2, molti). Questo sistema di numerazione è equivalente con il nostro fintantoché gli oggetti
da numerare sono 1 o 2, dopodiché la semplificazione del primo sistema rende i due sistemi non equivalenti: sarà possibile la trasformazione di un numero decimale in un numero di questo sistema
“primitivo” ma non viceversa.
PAG. 2.24
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CONVERGENZA DIGITALE
CONVERGENZA DIGITALE
Mentre l’uomo utilizza codici e simboli diversi in funzione
dell’informazione da rappresentare, all’interno dell’elaboratore tutte
le informazioni sono codificate utilizzando due soli simboli, 0 e 1.
Questo tipo di codifica è chiamata:
IMMAGINI
TESTO
"codifica binaria".
LAURA
SUONI
NUMERI
1
Ogni informazione, per quanto possa essere complessa, può
essere codificata utilizzando una serie di 0 e 1.
Il fatto che ogni tipo di informazione, per poter essere elaborata sul
computer, debba essere codificata in binario, in passato era stato visto come un vincolo, una necessità legata alle caratteristiche intrinseche dei computer. Solo di recente ci si è resi conto che, codificando
ogni informazione (anche analogica) in binario, si è di fatto raggiunta
una vera e propria:
32
1
E possiamo affermare che
STANDARDIZZAZIONE DEI METODI
DI RAPPRESENTAZIONE DELL’INFORMAZIONE
0
0
1
1
0
0
0
0
1 1 0 10 0 10
1
0
1
1
0
1
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
La disponibilità di un unico codice (“il codice binario”) per rappresentare informazioni anche molto diverse tra loro, associata ad uno strumento così potente come il computer, ha reso possibile una integrazione strettissima tra informazioni che eravamo abituati a considerare
lontane e nuove forme di comunicazione dalle caratteristiche e potenzialità appena esplorate:
• sugli elaboratori, con gli stessi strumenti, vengono manipolate informazioni di natura molto diversa (basta pensare che in un documento Word, oltre ai soliti dati numerici e testuali, è possibile inserire immagini e suoni);
• sulle reti digitali transitano contemporaneamente numeri, testo, immagini e suoni;
• macchine diverse possono parlare tra loro, unificate nel linguaggio
digitale, reale esperanto dell’informatica.
Nei prossimi paragrafi analizzeremo come, utilizzando la codifica binaria,
si possano codificare informazioni tra loro molto diverse.
PAG. 2.26
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
MOTIVAZIONE TECNOLOGICA PER L’USO DELLA CODIFICA
BINARIA
PERCHÉ LA CODIFICA BINARIA ?
IN UN COMPUTER TUTTA L’INFORMAZIONE È
CODIFICATA IN FORMA BINARIA
A SECONDA DEL SUPPORTO DI
MEMORIZZAZIONE UTILIZZATO, I VALORI
“0” E “1” SONO RAPPRESENTATI DA:
• DIFFERENTE CARICA
ELETTRICA
MEMORIE MAGNETICHE
Più precisamente, la necessità di utilizzare due soli simboli (che vengono associati a due stati fisici) deriva dalla semplicità e dalla sicurezza con cui, in un sistema fisico, è possibile distinguere uno stato
dall’altro. Se ad esempio si riuscisse, con la stessa semplicità e sicurezza, a realizzare dispostivi in grado di gestire tre stati, si potrebbero
realizzare computer basati su una logica ternaria.
La tecnologica attuale permette di avere 2 soli stati facilmente distinguibili l’uno dall’altro e trattabili con sufficiente economicità, precisione
e sicurezza.
DISPOSITIVI A
SEMICONDUTTORE
• DIFFERENTE STATO DI
POLARIZZAZIONE
MAGNETICA
I motivi per cui all’interno del computer si utilizza una logica
binaria per la codifica dell’informazione sono sostanzialmente
tecnologici, legati all’attuale architettura del computer.
128 MB
In relazione dispositivi fisici utilizzati questi due stati sono rappresentati da:
• una differente carica elettrica
(nei dispositivi a semiconduttore)
• un differente stato di polarizzazione
(nelle memorie magnetiche)
80 GB
1,4 MB
• un’alternanza luce-buio
(nelle memorie ottiche)
• ALTERNANZA LUCE BUIO
MEMORIE OTTICHE
600 MB
LA SCELTA DI LIMITARSI A
DUE SOLI STATI È DETTATA DA
MOTIVAZIONI TECNOLOGICHE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.28
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
IL BIT
IL BIT
L’UNITÀ ELEMENTARE DI
INFORMAZIONE GESTITA DA
UN COMPUTER È CHIAMATA
BIT
(BINARY DIGIT)
0
1
PROCESSO DI CODIFICA BINARIA
OGNI INFORMAZIONE,
PER QUANTO COMPLESSA,
PUÒ ESSERE RAPPRESENTATA,
SU UN COMPUTER, COME UNA
OPPORTUNA SEQUENZA DI BIT
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
La minima unità di informazione che un computer è in grado di gestire, è chiamata:
BIT
(BINARY DIGIT)
e convenzionalmente può assumere uno dei seguenti due valori:
0
1
Il BIT rappresenta il dato elementare utilizzato all’interno del computer
per codificare un’informazione: Mediante un BIT è possibile rappresentare informazioni elementari, come ad esempio:
“aperto”
“chiuso”,
“acceso”
“spento”
“nord”
“sud”
Considerati singolarmente i bit forniscono una minima capacità informativa, non utilizzabile praticamente. Per poter rappresentare informazioni più complesse è quindi necessario ricorrere a sequenze di
bit.
Ad esempio con 2 bit si possono rappresentare 4 informazioni differenti, codificando ognuna di esse con una delle seguenti coppie di bit
00, 01, 10, 11:
00
“nord”
01
“est”
10
“sud”
11
“ovest”
Con una opportuna sequenza di bit, la cui lunghezza dipende dalla
complessità dell’informazione che si intende rappresentare, è possibile codificare sul computer qualunque tipo di informazione.
Questo processo secondo cui si fanno corrispondere ad un informazione, una precisa configurazione di bit, prende il nome di:
CODIFICA BINARIA
DELL’INFORMAZIONE.
PAG. 2.30
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
IL BYTE
IL BYTE
MA, NELL’USO PRATICO DEL
CALCOLATORE, L’UNITÀ DI
INFORMAZIONE PIÙ
SIGNIFICATIVA È IL
Nell’uso pratico del calcolatore, ha assunto una rilevanza particolare l’aggregazione di 8 bit, che viene comunemente chiamata:
BYTE
La quantità di memoria di un computer si misura allora in BYTE2 e
nei suoi multipli.
Ma poiché nei moderni calcolatori, anche il byte è un’unità di misura
molto piccola, sono stati introdotti i suoi multipli:
1 BYTE
BYTE
0 1 0 1 1 0 0 1
= 8 bit
1 KILOBYTE (KB) = 1.024 BYTE = 210 BYTE (≅ 1.000 BYTE)3
1 MEGABYTE (MB)= 1.024 KB = 220 BYTE (≅ 1 milione di BYTE)
1 GIGABYTE (GB) = 1.024 MB = 230 BYTE (≅ 1 miliardo di BYTE)
1 TERABYTE (TB) = 1.024 GB = 240 BYTE (≅ 1.000 miliardi di BYTE)
(SEQUENZA DI 8 BIT)
E I SUOI MULTIPLI
KB
MB
GB
TB
= KILOBYTE = 1.024 BYTE
= MEGABYTE = 1.024 KB
≅ 1 MILIONE DI BYTE
= GIGABYTE = 1.024 MB
≅ 1 MILIARDO DI BYTE
= TERABYTE = 1.024 GB
≅ 1.000 MILIARDI DI BYTE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
2 Per dare un’idea di che cosa sia possibile rappresentare con un BYTE, come prima approssimazione si può pensare che un BYTE è la quantità di memoria necessaria per memorizzare un singolo carattere del nostro alfabeto.
3 Precisamente 210 byte sarebbe uguale a 1024 byte
PAG. 2.32
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
I SISTEMI DI NUMERAZIONE
SISTEMI DI NUMERAZIONE ADDITIVI
Prima di passare ad esaminare come le diverse informazioni possano
essere tutte rappresentate in codice binario, riprendiamo alcuni concetti
generali sui sistemi di numerazione, ovvero sui sistemi di codifica utilizzati per rappresentare la “quantità” di un insieme di oggetti
O MEGLIO
E NELL’ANTICHITÀ
LATINA
XXVI
X = DUE MANI
V = UNA MANO
I = UN DITO
EGIZIA
∩∩⏐⏐⏐
∩ = DUE MANI
⏐ = UN DITO
MAYA
=
⎯ = UNA MANO
= UN DITO
SISTEMI DI NUMERAZIONE ADDITIVI
I primi sistemi di numerazione utilizzati dall’uomo erano ben diversi dai
nostri. Essi infatti erano realizzati mediante l’incisione di un certo numero di aste su un qualche oggetto (ad esempio un bastone). In pratica si
basavano su un alfabeto costituito da un unico segno, l’asta, che veniva
ripetuto tante volte quanto era grande il numero che si voleva rappresentare. Questo sistema di numerazione, molto semplice quando si dovevano rappresentare piccoli numeri, diventava inutilizzabile quando
cresceva la numerosità degli oggetti da rappresentare. Un primo miglioramento fu quello di raggruppare le aste in gruppi uguali: poiché il primo
strumento di calcolo sono state le dita delle mani, i raggruppamenti più
usati furono quelli per 5 e per 10.
In quasi tutte le numerazioni usate in passato, come in quelle utilizzate
dai Maya, dagli Egizi, dai Romani, ritroviamo questo modo di numerare
che chiameremo: “additivo” (anche se con piccole varianti, dovute ai differenti segni utilizzati e al tipo di raggruppamento effettuato). Ad esempio,
gli egizi utilizzavano un alfabeto composto di due simboli:
∩
⏐
indicava le due mani e quindi valeva 10
indicava un dito e quindi valeva 1
Per indicare 34, con il sistema di numerazione egizio bisognava quindi
scrivere:
∩∩∩⏐⏐⏐⏐
SEMPLICE, MA POCO PRATICO CON NUMERI
GRANDI E DI DIFFICILE ELABORAZIONE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Nei sistemi di numerazione di tipo additivo, valgono le seguenti regole:
• il significato dei simboli che compongono un numero è indipendente
dalla posizione di tali simboli all’interno del numero stesso
• il valore finale si ottiene sommando i valori associati ad ogni simbolo.
PAG. 2.34
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
SISTEMI DI NUMERAZIONE POSIZIONALI
POSIZIONALE: IL
IN BASE 10:
SISTEMA DI NUMERAZIONE POSIZIONALE
Un sistema di numerazione additivo è molto semplice quando si debbano rappresentare numeri piccoli (e questa era probabilmente la
necessità dei tempi passati), mentre diventa poco pratico e difficilmente gestibile con numeri grandi: ma soprattutto non è adatto ad
essere elaborato.
SIGNIFICATO ATTRIBUITO A
CIASCUNA CIFRA È FUNZIONE
DELLA POSIZIONE CHE TALE
CIFRA OCCUPA ALL’INTERNO
DEL NUMERO
Un grosso salto di qualità si è fatto con l’adozione della numerazione
posizionale in cui:
INDICA IL NUMERO DI SIMBOLI
DIVERSI CHE POSSIAMO UTILIZZARE NEL SISTEMA DI NUMERAZIONE (0,1,2,3,4,5,6,7,8,9).....
In un sistema di numerazione posizionale, il valore di ogni cifra è
dato dal prodotto della cifra stessa per il peso della posizione. Il valore del numero è dato dalla somma dei valori delle singole cifre così
calcolate.
....E IL PESO DELLA POSIZIONE !
Ma come si fa a conoscere il “peso” associato alla posizione? Ogni
sistema di numerazione posizionale è caratterizzato dalla “BASE”
utilizzata per la numerazione. Nota che sia la “base”, è possibile
conoscere quanti simboli si possono utilizzare (“cifre”) per “scrivere”
un numero in quella base ed il peso associato ad ogni posizione.
2 2 2 2
×100
×101
×102
×103
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
uno stesso simbolo (che nei sistemi di numerazione si
è soliti chiamare “cifra”) assume diversi valori in base
alla sua posizione all’interno del numero
Supponendo di utilizzare una base avente valore N, si avrà che:
• un numero intero potrà essere scritto come una stringa di cifre
scelte da un insieme composto da N cifre (simboli) distinte:
0, 1,..., N-1;
• il valore di ogni una cifra dipenderà dalla sua posizione all'interno del numero; partendo da destra, il “peso” associato ad ogni
posizione sarà dato da:
1° posizione = N0 ( = 1 )
2° posizione = N1 ( = N)
3° posizione = N2
j° posizione = N j-1
• il valore delle singole cifre sarà calcolato moltiplicando il valore
della cifra per il peso della posizione ed il valore del numero sarà dato sommando i valori delle singole cifre.
PAG. 2.36
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
QUALE È IL NUMERO PIÙ GRANDE CHE SI PUÒ
RAPPRESENTARE CON N CIFRE
QUALE È IL NUMERO PIÙ GRANDE CHE SI PUÒ RAPPRESENTARE,
NELLA BASE X, CON N CIFRE
Un’altra domanda che ci possiamo porre è la seguente:
“Data un certa base N, qual è il massimo valore che possiamo rappresentare con J cifre?”
MAX = XN-1
La risposta è molto semplice ed è data dalla seguente formula:
IN CUI
X: BASE
N: NUMERO DI CIFRE
AD ESEMPIO CON
BASE
2
3
4
5
6
7
8
9
10
VALORE MAX = NJ - 1
in cui:
• N: è la base
• J: il numero di cifre utilizzate
2 CIFRE:
MASSIMO NUMERO
3
8
15
24
35
48
63
80
99
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Nella tabella riportata sullo schema a fianco, vengono riportati i valori massimi rappresentabili utilizzando 4 cifre, in funzione delle diverse basi utilizzabili.
Il sistema di numerazione che noi abitualmente utilizziamo (chiamato anche “arabico” in quanto introdotto in Europa dagli arabi nel corso del Medio Evo), ha la base uguale a 10 (il valore 10 deriva probabilmente dal numero di dita delle nostre mani).
Questo vuol dire che:
• per numerare si potranno utilizzare 10 diverse cifre (da 0 a 9);
• il valore di ogni posizione, partendo da destra, sarà una potenza di dieci ( a partire da destra abbiamo 100, 101, 102, 103,...).
Il sistema di numerazione posizionale, oltre ad essere più compatto,
permette anche una “manipolazione” (ovvero una elaborazione)
molto più efficiente dei numeri.
PAG. 2.38
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
LE DIVERSE BASI
BASE DIVERSA DA 10
È POSSIBILE NUMERARE GLI OGGETTI
UTILIZZANDO ALTRE BASI
AD ESEMPIO
COME SI
BASE SIMBOLI (CIFRE) UTILIZZATI
SCRIVE 10
2
3
4
5
.....
8
9
10
11
12
.....
16
0,1
1010
0,1,2
Ma sicuramente il sistema di numerazione posizionale più semplice
è quello in base 2 (“numerazione binaria”). Un sistema di fase 2, utilizza 2 soli simboli:
0, 1
e il peso della posizione J-esima è dato da 2j-1.
101
0,1,2,3
22
0,1,2,3,4
20
0,1,2,3,4,5,6,7
13
0,1,2,3,4,5,6,7,8
11
0,1,2,3,4,5,6,7,8,9
10
0,1,2,3,4,5,6,7,8,9,A
A
0,1,2,3,4,5,6,7,8,9,A,B
A
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
A
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Anche se il sistema di numerazione in base 10 è quello normalmente
utilizzato, dal punto di vista matematico, nulla ci impedirebbe di adottare un sistema di numerazione posizionale, basato su un diverso valore di base, per esempio 8 (come fa una tribù degli indiani,
che conta facendo riferimento agli spazi fra le dita delle mani). In
questo caso si utilizzerebbero 8 cifre e il peso della posizione Jesima sarebbe pari a 8j-1.
Un altro sistema di numerazione interessante (perlomeno per chi
opera nel mondo dell’informatica) è quello in base 16 (“sistema esadecimale”). In questo caso si utilizzeranno 16 cifre (come si può
vedere, per le restanti sei cifre si sono utilizzate le prime sei lettere
dell’alfabeto):
1, 2, 3, 4, 5, 6, 7, 8, 9, 0, A, B, C, D, E, F
e il peso della posizione J-esima è dato da 16j-1.
In questa tabella infine vediamo un esempio di come i numeri decimali possano essere convertiti nei corrispondenti numeri binari o
esadecimali e viceversa.:
DECIMALE
0
1
2
3
4
5
6
7
BINARIO
0
1
10
11
100
101
110
111
ESADECIMALE
0
1
2
3
4
5
6
7
DECIMALE
BINARIO
8
9
10
11
12
13
14
15
1000
1001
1010
1011
1100
1101
1110
1111
ESADECIMALE
8
9
A
B
C
D
E
F
PAG. 2.40
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
PASSAGGIO DA BASE “X” A BASE 10
DA BASE 2 A BASE 10
1011
= 1×23 + 0×22 + 1×21 + 1×20 =
= 1×8 + 0×4 + 1×2 + 1×1 =
=8+0+2+1=
= 11
PASSAGGIO DA BASE “X” A BASE 10
“Ma una volta che si abbia un numero codificato in base diversa
dalla base 10, è possibile trasformarlo in un numero decimale ?”
La risposta a questa domanda è senz’altro positiva ed anzi, il passaggio da una generica base X alla base 10, è anche molto semplice. Lo illustreremo con un paio di esempi.
Nel primo esempio supponiamo di voler convertire, in decimale, il
seguente numero binario:
1 0 1 1
Definito il peso delle singole cifre:
1 0 1 1
23 22 2 1 2 0
possiamo calcolare il corrispondente valore decimale moltiplicando il
valore di ogni cifra per il suo peso e sommando i totali parziali ottenuti:
( 2 3 x 1 ) + ( 2 2 x 0) + ( 2 1 x 1) + ( 2 0 x 1)
L’espressione, dopo alcuni semplici passaggi, passaggi diventa:
8 + 0 + 2 + 1 = 11
DA BASE 16 A BASE 10
B7A
= B×162 + 7×161 + A×160 =
= B×256 + 7×16 + A×1 =
= 11×256 + 7×16 + 10×1 =
= 2816 + 112 + 10 =
= 2938
(il corrispondente valore decimale)
Nel secondo esempio trasformiamo, in formato decimale, il numero
esadecimale B7A. Applicando lo stesso metodo si ha:
B
7
A
162
161
160
per cui possiamo scrivere:
(16 2 x B) + (16 1 x 7) + (16 0 x 10)
che con semplici passaggi diventa:
(256 x 11) + (16 x 7) + (1 x 10)
e quindi
2816 + 112 + 10 = 2938
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
(il corrispondente valore decimale)
PAG. 2.42
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
PASSAGGIO DA BASE 10 A BASE “X”
1
2
6
0
2
3
1
2
1
1
Leggermente più articolato, ma altrettanto meccanico, è il passaggio
inverso. Anche in questo caso partiamo da un esempio per spiegare come si effettua la conversione di base.
Supponiamo di voler trovare il numero binario corrispondente ad un
numero decimale X. La regola è la seguente:
I. bisogna dividere X per 2,
II. quindi si procede a dividere per due ogni quoziente successivo,
finché il quoziente stesso non diventi uguale a zero;
III. la rappresentazione binaria del numero, si ottiene scrivendo i resti delle divisioni in ordine inverso a come è stato effettuato il calcolo.
DA BASE 10 A BASE 2
13
PASSAGGIO DA BASE 10 A BASE “X”
2
0
Ad esempio, per convertire in binario il numero decimale 13 si procede così:
Passo 1°
Passo 2°
Passo 3°
Passo 4°
1) BASTA DIVIDERE SEMPRE PER DUE FINCHÉ IL
QUOZIENTE NON È ZERO
2) LA SEQUENZA DI VALORI DEI RESTI, SCRITTI IN
ORDINE INVERSO, È LA RAPPRESENTAZIONE
BINARIA DEL NUMERO CERCATO
Divisione
13/2
6/2
3/2
1/2
Quoziente
6
3
1
0
Resto
1
0
1
1
A questo punto, leggendo i resti dal basso verso l’alto, si ottiene il
numero binario cercato:
1 1 0 1
1310=11012
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.44
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
IL VALORE DI UN NUMERO A SECONDA DELLA BASE
MA ALLORA QUANTO VALE 101 ?
Riepiloghiamo sinteticamente i punti principali relativamente ai sistemi di numerazione posizionali:
1012 = 1×22 + 0×21 + 1×20 =
5
1013 = 1×32 + 0×31 + 1×30 =
10
• nel linguaggio corrente la base non viene mai comunicata, in
quanto si dà per scontato l’utilizzo del sistema decimale (e quindi
della base 10);
17
• la base 10 viene utilizzata dall’Uomo per motivi legati alla sua
conformazione fisica (le 10 dita delle mani); questo non significa
che in alcune situazioni non sia più conveniente utilizzare una base diversa (ad esempio nel mondo dei computer è più conveniente utilizzare la base binaria);
1014 = 1×42 + 0×41 + 1×40 =
.....
• la conoscenza del reale valore di un numero, dipende dalla conoscenza del valore della base utilizzata;
• Il passaggio dei numeri fra una base e l’altra è sempre possibile.
10110 = 1×102 + 0×101 + 1×100 = 101
.....
10116 = 1×162 + 0×161 + 1×160 = 257
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.46
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
OPERAZIONI IN BINARIO
BINARIO È BELLO !
Parlando del sistema di numerazione binario, abbiamo affermato
che questo sistema, basato su 2 soli simboli, è il “più semplice”.
Verifichiamo la veridicità di questa affermazione, analizzando come
“funzionano” alcune normali operazioni aritmetiche, quando vengono applicate ai numeri binari.
SOMMA: LE REGOLE
0+0
=
LA SOMMA
1
1+0
=
1
0+1
=
1
1+1
= 10
0 COL RIPORTO DI 1
L’operazione di addizione segue le stesse regole che usiamo per i
numeri decimali, solo che qui è molto più semplice in quanto si
hanno in totale solo 4 possibili combinazioni:
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 0 con riporto di 1
Proviamo, come esempio, a sommare due numeri binari, :
ESEMPIO:
0
0
1
1
0
0
1
1
0
0
0
1
1
0
0
1
1
0
0
1
1
1
0
1
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
h
g
f
e
d
c
b
a
0
1
1
0
1
1
0
1
+
0
0
1
0
0
1
1
0
=
1
0
0
1
0
0
1
1
Parendo da destra abbiamo che:
a) 1 più 0 fa 1
b) 0 più 1 fa 1
c) 1 più 1 fa 0 con il riporto di 1
d) 1 più 0 fa 1, più 1 che riportavo fa 0 con il riporto di 1
e) 0 più 0 fa 0, più 1 che riportavo fa 1
f) 1 più 1 fa 0 con il riporto di uno
g) 1 più 0 fa 1, più 1 che riportavo fa 0 con il riporto di 1
h) 0 più 0 fa 0, più 1 che riportavo fa 1
PAG. 2.48
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
LA MOLTIPLICAZIONE
MOLTIPLICAZIONE: LA TABELLINA
×
0
1
0
0
0
LA MOLTIPLICAZIONE
Anche la moltiplicazione tra due numeri binari utilizza le stesse regole usate per la moltiplicazione decimale, ma ancora una volta il
procedimento è molto più semplice in quanto, al posto della classica
tabella pitagorica, si usa una tabellina molto più semplice:
0
0
1
1
1
0
1
×
×
×
×
0
1
0
1
0
= 0
= 0
= 1
=
Anche in questo caso calcoliamo, come esempio, il prodotto tra due
numeri binari:
1
ESEMPIO:
1
1
1
0
0
0
0
0
1
1
1
1
0
1
1
1
0
0
0
1
1
X
1
0
=
0
0
0
0
1
0
1
1
1
0
1
1
0
Notiamo che il calcolo dei prodotti parziali è estremamente semplice: se la cifra considerata del moltiplicatore vale 0, allora il prodotto
parziale sarà uguale a tutti 0, mentre se vale 1 sarà uguale al moltiplicando.
0
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.50
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
PERCHÉ È INTERESSANTE LA NUMERAZIONE
ESADECIMALE ?
UN BYTE È SCOMODO DA RAPPRESENTARE
00101010
MA UN BYTE PUÒ ESSERE DIVISO IN 2 SEMI-BYTE
0010
0
1
2
3
4
0101
0110
0111
1000
1001
5
6
7
8
9
1010
1011
1100
1101
1110
1111
A
B
C
D
E
F
QUINDI UN BYTE PUÒ ESSERE RAPPRESENTATO
CON 2 CIFRE ESADECIMALI (SINTETICITÀ DELLA
RAPPRESENTAZIONE)
0010
1010
2
A
Prima di affrontare la problematica della codifica binaria, apriamo
una parentesi sulla numerazione esadecimale, spiegando il perché
questa numerazione è tanto interessante per chi opera nel mondo
dell’informatica. E’ stato già sottolineato che il byte è l’elemento di
memorizzazione normalmente utilizzato. Un aspetto importante, per
chi deve operare con informazioni binarie, è quello di trovare un
modo compatto per rappresentare il contenuto del byte, senza dover ricorrere alla completa enumerazione di tutti gli 8 bit:
00100110
1010
UTILIZZANDO UN NUMERIO ESADECIMALE È
POSSIBILE RAPPRESENTARE UN SEMI-BYTE
CON UNA CIFRA ESADECIMALE (FACILITÀ DI
CONVERSIONE DALLA BASE 2 ALLA BASE 16)
0000
0001
0010
0011
0100
PERCHÉ È INTERESSANTE LA NUMERAZIONE
ESADECIMALE ?
IN BINARIO
IN ESADECIMALE
Ora, se si divide il byte in 2 parti (“semibyte”), otteniamo due raggruppamenti di 4 bit, ognuno dei quali può rappresentare 16 (=24)
configurazioni diverse. L’unico modo per rappresentare un semibyte
con un solo simbolo, è proprio quello di usare un sistema di numerazione in base 16:
0000
0001
0010
0011
0100
0101
0110
0111
0
1
2
3
4
5
6
7
1000
1001
1010
1011
1100
1101
1110
1111
8
9
A
B
C
D
E
F
Utilizzando questa tabellina, un byte può essere comodamente rappresentato con le due equivalenti cifre esadecimali:
10011100 9CH
00110111 37H
Allo stesso modo, anche il passaggio inverso, è un’operazione facile e veloce:
DAH 11011010
Per evitare confusioni con i numeri decimali, i numeri esadecimali
sono in genere seguiti dalla lettera “H”.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.52
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
LA CODIFICA BINARIA
DELL’INFORMAZIONE
TUTTA L’INFORMAZIONE È BINARIA
1 1 0 10 0 10
1
1
1
0 1
0
1
0
0
In questo capitolo analizzeremo come ogni informazione, per quanto
complessa, possa sempre essere rappresentata con una opportuna
sequenza di bit. In particolare si cercherà di capire come è possibile rappresentare con due soli simboli, 0 e 1, informazioni tanto diverse come:
NUMERI
TESTI
IMMAGINI
SUONI
Mentre questi vari tipi d’informazioni vengono codificati dall’uomo
utilizzando simboli e codici molto diversi tra loro, all’interno del
computer sono tutti rappresentato in un formato binario. Questo
processo, chiamato anche:
CODIFICA BINARIA DELL’INFORMAZIONE,
1
0
permette di ottenere una rappresentazione uniforme di tutte le informazioni.
0
1
1
Ci piace in tal senso ricordare Leibnitz, che vedeva nella notazione
binaria “un’immagine della creazione” e sosteneva:
0
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
0
“il calcolo binario, che utilizza 0 e 1, a ricompensa della maggior
lunghezza è il più fondamentale per la scienza ed è all’origine di
nuove scoperte (…) la cui ragione è che, allorché i numeri sono ridotti ai principi più semplici, e cioè allo 0 e 1, appare ovunque un
ordine meraviglioso”
PAG. 2.54
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DEI CARATTERI
I CARATTERI CHE COSTITUISCONO UN TESTO
SONO, DI NORMA, CLASSIFICATI IN TRE CATEGORIE:
• CARATTERI
ALFANUMERICI
• SEGNI
• CARATTERI DI
CONTROLLO
A,B,...,Z,a,b,...,z,0,1,2...9
,.;:!?”%&()<>=+-*/
CODICI PER LA TRASMISSIONE O
IL CONTROLLO DELLE STAMPE
LA CODIFICA DEI CARATTERI
Per poter comunicare con l’elaboratore, usando il nostro linguaggio, il
primo problema che ci si presenta è quello di rappresentare il nostro alfabeto. In base al numero di caratteri che si vogliamo rappresentare, sarà necessario individuare il numero minimo di bit che ne permetta la
rappresentazione. Se per esempio, ci si accontentasse di rappresentare
le sole lettere dell’alfabeto (maiuscole), basterebbero 5 bit per ogni carattere. Per codificare l’insieme dei simboli usati dal nostro alfabeto (o
meglio quello anglosassone), comprendendo le maiuscole e le minuscole, i numeri ed i segni d’interpunzione, sono necessari almeno 7 bit (128
configurazioni differenti).
Nella tabella seguente è riportato un esempio di codifica secondo lo
standard ASCII, che utilizza appunto 7 bit. La prima colonna riporta un
carattere dell’alfabeto (o una cifra o un segno). La seconda e la terza
colonna riportano la codifica ASCII corrispondente, espressa rispettivamente, in codifica esadecimale e in codifica binaria.
AMERICAN STANDARD CODE FOR INFORMATION INTERCHANGE
CAR
LA CODIFICA DI UN CARATTERE:
• UTILIZZA UNA SEQUENZA DI BIT
• IL NUMERO DI CARATTERI RAPPRESENTATI
DIPENDE DAL NUMERO DI BIT UTILIZZATI
• È UNA CONVENZIONE TRA I PRODUTTORI
• PUÒ ESSERE CAUSA DI INCOMPATIBILITÀ
TRA ELABORATORI DIVERSI (NECESSITÀ DI
CONVERSIONI)
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
HEX
BINARIA
CAR
HEX
BINARIA
...
...
.....
6
36
00110110
SPAZIO
!
“
#
$
%
&
‘
(
)
*
+
,
.
/
0
1
2
3
4
5
20
21
22
23
24
25
26
27
28
29
2A
2B
2C
2D
2E
2F
30
31
32
33
34
35
00100000
00100001
00100010
00100011
00100100
00100101
00100110
00100111
00101000
00101001
00101010
00101011
00101100
00101101
00101110
00101111
00110000
00110001
00110010
00110011
00110100
00110101
7
8
9
:
;
<
=
>
?
@
A
B
C
D
E
F
G
H
I
J
K
...
37
38
39
3A
3B
3C
3D
3E
3F
40
41
42
43
44
45
46
47
48
49
4A
4B
...
00110111
00111000
00111001
00111010
00111011
00111100
00111101
00111110
00111111
01000000
01000001
01000010
01000011
01000100
01000101
01000110
01000111
01001000
01001001
01001010
01001011
.....
PAG. 2.56
INFORMATICA
CODIFICA DEI CARATTERI
IN GENERE UN CARATTERE È CODIFICATO
IN UN BYTE UTILIZZANDO LA CODIFICA:
• ASCII (AMERICAN STANDARD CODE FOR INFORMATION
INTERCHANGE) CHE UTILIZZA SOLO 7 BIT DEGLI 8
DISPONIBILI RIUSCENDO COSÌ A CODIFICARE
SOLO 128 CARATTERI DIVERSI
•
ASCII ESTESO CHE UTILIZZA TUTTI E 8 I
BIT, CODIFICANDO 256 CARATTERI DIVERSI
•
EBCIDIC A 8 BIT, UTILIZZATO DAI COMPUTER
IBM
• UNICODE POICHÉ 256 CARATTERI SONO
INSUFFICIENTI PER LE ESIGENZE DEI DIVERSI
SISTEMI DI SCRITTURA E DI RAPPRESENTAZIONE
SIMBOLICA, È STATO PROPOSTO QUESTO NUOVO
CODICE A 16 BIT, CHE PERMETTE DI CODIFICARE
CIRCA 65.000 CARATTERI DIVERSI
CAP. 2 - LA CODIFICA BINARIA DEI DATI
GLI STANDARD PER CODIFICARE I CARATTERI
Un aspetto importante della codifica è che sia una convenzione accettata da tutti gli utilizzatori. Per tale ragione, a livello internazionale, sono
stati definiti degli standard per la rappresentazione dei caratteri. La situazione degli standard di codifica dei caratteri è la seguente.
La codifica ASCII Standard - (American Standard Code for Information
Interchange) codifica un carattere utilizzando un byte in cui il primo bit è
sempre lasciato uguale a 0; è lo standard più diffuso ed accettato, ed
è normalmente utilizzato nel mondo dei personal computer.
La codifica ASCII Esteso utilizza tutti gli 8 bit del byte, riuscendo così
a codificare ulteriori 128 caratteri (per un totale di 256).
I caratteri aggiuntivi permettono di raffigurare alcuni caratteri speciali
dei vari alfabeti, i simboli dell’alfabeto greco e alcuni simboli scientifici. Mentre la codifica ASCII standard è riconosciuta ed utilizzata da
tutti i produttori e in tutti i paesi del mondo, attualmente questo non è
vero per la codifica ASCII estesa, che può essere diversa da paese a
paese e da produttore a produttore, e può essere causa di incompatibilità tra elaboratori diversi.
La codifica EBCDIC - (Extended Binary Coded Decimal Interchange
Code) utilizza un byte per rappresentare 256 caratteri; questa codifica è stata sviluppata da IBM ed è utilizzata sui minicomputer (modelli
AS/400) e sui mainframe; non è usata sui personal; la differenza sostanziale di questo codice rispetto al codice ASCII è il diverso modo
con cui sono codificati i numeri.
Anche utilizzando 256 caratteri non è possibile rappresentare i simboli dell’alfabeto di altre lingue, come l’arabo, il russo, il giapponese,
che hanno un alfabeto completamente diverso dal nostro e composto
da molti più simboli. Per rispondere a questo problema, in questi ultimi anni si è stato proposto un nuovo tipo di standard chiamato
UNICODE, che, utilizzando 16 bit, è in grado di codificare circa
65.000 simboli diversi.
Di fatto la presenza di più standard, anche se universalmente accettati e
riconosciuti, crea dei problemi quando si mettono in comunicazione due
elaboratori che utilizzano codifiche diverse. In particolare, in quest’ultimo
caso, ogni volta che si debbano trasferire dati da un sistema all’altro,
occorre eseguire prima una trascodifica dei dati stessi.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.58
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DEI NUMERI IN ASCII
CODIFICA DEI NUMERI IN ASCII
Dopo aver visto (cfr. tabella ASCII) che all’interno del codice ASCII
sono rappresentate anche le cifre decimali, la prima idea è quella di
rappresentare un numero come una sequenza di cifre codificate secondo lo standard ASCII (allo stesso modo in cui una parola può
essere pensata composta da una sequenza di caratteri).
OGNI CIFRA È CODIFICATA CON IL
CORRISPONDENTE CARATTERE ASCII
Con questo sistema il numero 1951 si può rappresentare con una
sequenza di 4 byte:
1
1
9
5
1
00110001
00111001
00110101
00110001
9
5
1
00110001 00111001 00110101 00110001
Se da una parte tale codifica, utilizzando lo standard ASCII, è riconosciuta da ogni tipo di elaboratore, dall’altra presenta alcuni gravi
inconvenienti:
• è una codifica non efficiente in termini di occupazione di memoria:
infatti, come si può notare, i primi 4 bit sono sempre uguali, in tutte le cifre;
• non è adatta per essere elaborata numericamente, e questo è un
problema ben più grave.
• SPRECA SPAZIO (EFFICIENZA)
• NON È ELABORABILE NUMERICAMENTE
(EFFICIENZA)
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.60
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DEI NUMERI NATURALI
0, 1, 2, 3, 4, 5, 6, 7, 8,....
LA SOLUZIONE PIÙ "RAGIONEVOLE" È QUELLA
DI CODIFICARE I NUMERI IN FORMATO BINARIO
SI POSSONO
CODIFICARE I NUMERI
INTERI COMPRESI TRA
CON
1 BYTE
0
2 BYTE
0
4 BYTE
0
255
65.535
4.294.967.295
CODIFICA DEI NUMERI NATURALI
Riflettendo sui concetti presentati, relativi ai diversi sistemi di numerazione, si scopre che esiste un modo più naturale ed efficiente per
rappresentare i numeri. Tale metodo si basa sul fatto che un numero decimale può essere facilmente convertito in un equivalente numero binario e rappresentato direttamente in termini di 0 e 1.
Usando tale metodo è possibile rappresentare facilmente qualunque numero naturale (ossia un numero intero positivo). Tale rappresentazione oltre ad essere decisamente molto più compatta di
quella vista in precedenza, è ovviamente utilizzabile direttamente
all’interno del computer, per l’esecuzione delle operazioni aritmetiche.
Un ultimo punto che si vuole mettere in evidenza, riguarda il numero di bit che debbano essere utilizzati per la rappresentazione binaria dei numeri. Vale la seguente regola (cfr. sistemi di numerazione):
con n cifre binarie è possibile rappresentare i numeri da 0 a 2n-1
Nel momento in cui si fissa il numero di bit destinati alla rappresentazione di un numero, automaticamente si fissa anche il numero
massimo gestibile con quella rappresentazione.
IN GENERALE CON
Ma cosa succede se durante una elaborazione si va oltre il massimo numero rappresentabile?
N BIT
Quando durante un’operazione aritmetica, il totale va oltre il valore
massimo rappresentabile con la configurazione di bit utilizzata, si
genera una condizione di overflow (ossia “travaso”) in quanto si va
oltre il numero di cifre destinato alla rappresentazione. Di norma
questa condizione genera una situazione d’errore che deve essere
gestita dal programma.
SI POSSONO CODIFICARE I NUMERI
NATURALI COMPRESI TRA
0
2N-1
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.62
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DEI NUMERI INTERI
...,-4, -3, -2, -1, 0, 1, 2, 3, 4,....
POSITIVI E NEGATIVI
SI MANTIENE LA CODIFICA BINARIA, MA
OCCORRE RISERVARE UN BIT PER
IL SEGNO
NUMERO
1° SOLUZIONE
2°SOLUZIONE
POSITIVO
1 BIT PER SEGNO
COMPLEMENTO A 2
(FACILE DA
LEGGERE)
(FACILE DA
ELABORARE)
CODIFICA DEI NUMERI INTERI
Abbiamo visto come, utilizzando la numerazione binaria, si possano
facilmente rappresentare i numeri naturali. Ma per le normali necessità elaborative è necessario avere la possibilità di rappresentare anche i numeri negativi (in sostanza i numeri interi).
Supponendo di avere N bit a disposizione per la rappresentazione
del numero, una prima idea è quella di destinare 1 bit per rappresentare il segno e gli altri N-1 bit per rappresentare il valore assoluto del numero, codificato in forma binaria. Ad esempio si potrebbe
stabilire la convenzione che il primo bit a sinistra, se uguale a zero
indica un segno positivo, mentre se uguale a 1, un segno negativo.
Questa soluzione presenta due problemi che la rendono poco utilizzata nella pratica:
• in primo luogo vi sono due rappresentazioni per lo zero, una con il
segno positivo (00000000) e l’altra con il segno negativo (10000000);
• ma il problema maggiore è che una rappresentazione di questo tipo
non è elaborabile con facilità.
Una diversa rappresentazione dei numeri negativi, che elimina questi problemi, è quella che prende il nome di:
COMPLEMENTO A DUE
00001001
10001001
11110111
IN GENERALE CON
N BIT
SI POSSONO CODIFICARE I NUMERI
INTERI COMPRESI TRA
- 2N-1
2N-1-1
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
e che è definita dalle seguenti regole:
• il bit più a sinistra è riservato per il segno: se vale 0 indica un
numero positivo, se vale 1, un numero negativo
• i numeri positivi vengono codificati, nei restanti N-1 bit, con le
stesse modalità dei numeri naturali;
• la rappresentazione di un numero negativo si ottiene attraverso i
seguenti tre passi:
- si codifica il valore assoluto del numero, ovvero
come se fosse positivo (ad es. 00000101)
- si invertono i bit in tale rappresentazione, mettendo
0 dove c’è 1 e viceversa (ad es. 11111010)
- si somma 1 al risultato ottenuto al passo precedente (ad es. 11111011)
PAG. 2.64
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DEI NUMERI INTERI: UN ESEMPIO
N. DEC
SEGNO
COMPL. 2
7
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
-6
-7
-8
0111
0110
0101
0100
0011
0010
0001
0000
1001
1010
1011
1100
1101
1110
1111
***
0111
0110
0101
0100
0011
0010
0001
0000
1111
1110
1101
1100
1011
1010
1001
1000
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
I NUMERI NEGATIVI CODIFICATI IN COMPLEMENTO A 2
Il vantaggio di usare la rappresentazione in “complemento a 2” è
quello di poter calcolare la differenza tra due numeri utilizzando solamente l’operazioni di somma. Vediamo, in un esempio, come funziona in pratica questo metodo. Supponiamo di voler calcolare:
5-3
Utilizzando la rappresentazione in complemento a 2 è come se calcolassimo:
5 + (-3).
Elenchiamo i passi attraverso cui si procede:
I) come primo passo codifichiamo 5; ricordiamo che il primo bit deve
essere uguale a 0, mentre i restanti bit codificheranno il valore 5; il risultato sarà:
00000101
II) quindi codifichiamo -3 utilizzando la codifica in complemento a 2; per
prima cosa codifichiamo il valore 3:
00000011
poi invertiamo i segni:
11111100
e infine sommiamo 1 al numero risultante:
11111101
III) Ora possiamo sommare i due valori:
00000101 +
11111101 =
100000010
in cui il bit cerchiato è il bit di overflow e va ignorato.
Il risultato è quindi 00000010 e cioè 2.
PAG. 2.66
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA BINARIA VS. CODIFICA ASCII
UN NUMERO PUÒ ESSERE RAPPRESENTATO
• CODIFICANDO TUTTE LE SUE CIFRE
COME SE FOSSERO CARATTERI ASCII
• CON LA CODIFICA BINARIA
NUMERO
INTERO
CODIFICA
BINARIA
CODIFICA
ASCII
4
0000 0100
0011 0100
18
0001 0010
0011 0001
0011 1000
123
0111 1011
CODIFICA BINARIA
0011 0001
0011 0010
0011 0011
• COMPATTA
• ADATTA PER
FARE I CALCOLI
CODIFICA ASCII
• ADATTA PER
INPUT/OUTPUT
CODIFICA BINARIA VS. CODIFICA ASCII
Nello schema della figura a fianco, troviamo a confronto i due sistemi appena visti per la codifica di un numero. Abbiamo già discusso dei vantaggi e degli svantaggi dell’uno e dell’altro metodo.
Vogliamo ora aggiungere un’ulteriore considerazione sulla codifica
da utilizzare quando un dato deve essere inviato ad un dispositivo
di input/output (“I/O device”). Prendiamo a riferimento la stampante
collegata ad un personal computer. Tutti dati che vengono inviati
alla stampante devono essere necessariamente codificati come caratteri nello standard ASCII. E’ questa infatti l’unica codifica universalmente adottata e riconosciuta dai dispositivi periferici.
Per i dati di tipo testo questo fatto non comporta alcun tipo di problema (in quanto sono già codificati, all’interno del computer, in
formato ASCII), ma per i dati numerici la cosa cambia: ogni volta
che un dato numerico (normalmente codificato all’interno
dell’elaboratore in un formato binario) deve essere inviato ad un dispositivo di output, come appunto una stampante o un video, deve
essere prima trascodificato in formato ASCII.
Anche in fase di input dei dati c’è lo stesso tipo di problema: tutti i
dati numerici acquisiti tramite un dispositivo di input, come una tastiera, sono in realtà letti come una sequenza di cifre, codificate in
formato ASCII: prima di poter essere elaborati devono pertanto essere trascodificati in formato binario.
Questo fatto non è da sottovalutare: in alcuni tipi di applicazioni (per
esempio quelle relative alla gestione aziendale) l’attività di input/output è normalmente maggiore dell’attività di calcolo vera e
propria. Questo significa che l’attività appena descritta di ricodifica
da binario ad ASCII e viceversa può diventare critica.
• NON PUÒ ESSERE
ELABORATA
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.68
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
UN COMPROMESSO: LA CODIFICA BCD (BINARY
CODE DECIMAL)
OGNI CIFRA DEL NUMERO VIENE CODIFICATA
CON 4 BIT (SEMIBYTE) CHE RAPPRESENTANO
LA CIFRA IN CODICE BINARIO
UN COMPROMESSO: LA CODIFICA BCD
(BINARY CODE DECIMAL)
Una soluzione al problema (prospettato nella pagina precedente) di
trovare una codifica ottimale per i dati numerici, la si può trovare
nell’uso della codifica BCD (binary code decimal). Questo codifica
rappresenta infatti un ottimo compromesso tra due opposte esigenze:
• COMPATTEZZA DELLA
CODIFICA
• SEMPLICITÀ E VELOCITÀ
DI ELABORAZIONE
• UTILIZZABILITÀ PER
OPERAZIONI DI I/O
0
0000
5
0101
1
0001
6
0110
2
0010
7
0111
Nello schema a fianco viene illustrato come vengono codificati i
numeri utilizzando la codifica BCD.
3
0011
8
1000
Praticamente ogni cifra del numero viene codificata con 4 bit
(semibyte) secondo la tabella seguente.
4
0100
9
1001
NUMERO
INTERO
CODIFICA
BINARIA
CODIFICA
ASCII
CODIFICA
BCD
18
0001 0010
0011 0001
0011 1000
0001 1000
123
0111 1011
0011 0001
0011 0010
0011 0011
0000 0001
0010 0011
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
0
1
2
3
4
5
6
7
8
9
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
(peraltro, ad una più attenta osservazione, si scopre che questi 4 bit altro
non sono che la rappresentazione della cifra stessa in codice binario).
Nel caso di un numero intero (con segno), un semibyte viene poi
riservato alla rappresentazione del segno.
PAG. 2.70
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
BCD VS. BINARIO
LA CODIFICA BCD DI UN NUMERO:
OCCUPA PIÙ SPAZIO IN MEMORIA, MA È LA
METÀ DELLA CODIFICA ASCII
ES. IL MASSIMO NUMERO CHE SI PUÒ RAPPRESENTARE
CON UN BYTE È:
11111111
10011001
00111001
255
99
9
in binario
in BCD
in ASCII
NON È UTILIZZABILE DIRETTAMENTE PER
OPERAZIONI DI I/O, MA LA CONVERSIONE È
MOLTO PIÙ SEMPLICE CHE PER IL BINARIO
BCD VS. BINARIO
A questo punto viene da chiedersi se c’era proprio necessità di inventarsi un’ulteriore modalità di codifica e, nel caso affermativo quali siano i vantaggi. Vediamoli.
1. Un numero codificato in BCD occupa più spazio in memoria
dell’equivalente codifica in binario, ma comunque occupa sempre
la metà di un numero che utilizzi la codifica ASCII.
Ad es. il massimo numero che si può rappresentare con un byte è:
11111111
- in binario: 255
99
10011001
- in BCD:
9
00111001
- in ASCII:
2. un numero in BCD non è utilizzabile direttamente per le operazioni di I/O, ma la conversione in formato ASCII è di gran lunga
più facile e veloce rispetto al formato binario puro. E questo abbiamo visto essere un aspetto di particolare rilevanza quando si
devono effettuare pochi calcoli ma molte stampe (EDP).
3. Infine, mentre un numero in formato ASCII per essere elaborato
vie sempre convertito in binario, esistono particolari unità di elaborazione in grado di eseguire calcoli direttamente con numeri in
formato BCD.
BASTA PRENDERE IL SEMI-BYTE CHE RAPPRESENTA UNA
CIFRA BCD ED AGGIUNGERE A SINISTRA “0011”
PERMETTE L’ESECUZIONE DIRETTA DELLE
OPERAZIONI MATEMATICHE, A PATTO CHE
L’UNITÀ DI ELABORAZIONE SIA IN GRADO
DI ESEGUIRE CALCOLI CON NUMERI IN
FORMATO BCD
MENTRE IL FORMATO ASCII NON È ELABORABILE.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.72
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
COME SI PUÒ RAPPRESENTARE UN NUMERO
INTERO ?
COME SI PUÒ RAPPRESENTARE UN NUMERO INTERO ?
A questo punto alla domanda:
“Come si può rappresentare un numero all’interno dell’elaboratore?”
dovremmo essere tutti in grado di rispondere con sicurezza. In funzione dell’uso che andremo a fare, possiamo codificarlo:
• in binario
BINARIO
• in BCD
00001101
(0DH)
• in ASCII
BCD
13
00010011
(13H)
ASCII
00110001
00110011
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
(31H)
(33H)
PAG. 2.74
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
NUMERI REALI: N. ESPONENZIALE
DA UN PUNTO DI VISTA MATEMATICO,
UN NUMERO REALE PUÒ ESSERE ESPRESSO
IN NOTAZIONE ESPONENZIALE
1856,8
0,18568 E+4
CHE SIGNIFICA 0,18568 × 104
IN CUI
0,18568
+4
PRO:
SI CHIAMA
SI CHIAMA
NUMERI REALI: LA NOTAZIONE ESPONENZIALE
Finora è stata trattata la rappresentazione dei numeri interi. Peraltro, poiché la rappresentazione di un numero avviene su un sistema
fisico, utilizzando un numero ben definito di bit, questo pone di conseguenza un limite al numero massimo rappresentabile.
Cerchiamo ora di capire come sia possibile:
• rappresentare i numeri reali, come ad esempio 1856,8, che non
è rappresentabile in nessuna delle codifiche viste in precedenza;
• rappresentare i numeri molto grandi, mantenendo l’ordine di
grandezza e accontentandoci di una precisione limitata, senza dover riservare centinaia di bit in memoria per la loro rappresentazione.
Questo tipo di problema si risolve da un punto di vista matematico. Infatti, poiché un numero come 1856,8 può essere rappresentato mediante quella che si chiama notazione esponenziale,
1856,8
0 , 1 8 5 6 8 E+4
(che equivale a 0,18568 × 104)
MANTISSA
ESPONENTE
SI POSSONO RAPPRESENTARE
NUMERI MOLTO GRANDI (O MOLTO
PICCOLI) CON POCHE CIFRE
CONTRO: SI PUÒ PERDERE IN PRECISIONE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
in cui
• 0,18568 si chiama mantissa
• + 4 si chiama esponente
il numero stesso può essere codificato attraverso una coppia di
numeri interi (18568 e 4) che indicano rispettivamente la mantissa e
l’esponente .
Con la notazione esponenziale si possono rappresentare, con poche cifre, anche numeri molto grandi (o molto piccoli), anche se
questo può andare a scapito della precisione. Per fare un esempio,
supponiamo di voler rappresentare il numero:
1.000.000.000.000.000.000.000
Utilizzando il metodo della notazione esponenziale noi possiamo
ricondurlo alla forma seguente: 0,1 E+22. Con pochissime cifre è stato
possibile rappresentare un numero grandissimo che, con qualunque
altro tipo di codifica, avrebbe richiesto un numero di bit.
PAG. 2.76
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
NUMERI REALI: LA CODIFICA
CODIFICA DEI NUMERI REALI
UNA POSSIBILE RAPPRESENTAZIONE (FLOATING
POINT) DI UN NUMERO REALE NELL’ELABORATORE
CONSISTE NEL CODIFICARE:
• LA MANTISSA SU 3 BYTE
• L’ESPONENTE SU 1 BYTE
Una possibile rappresentazione di un numero reale, espresso in notazione esponenziale, avendo, ad esempio, disponibili 32 bit, potrebbe essere la seguente:
• 1 bit per il segno della mantissa
• 23 bit per il valore assoluto della mantissa
• 1 bit per il segno dell’esponente
• 7 bit per il valore assoluto dell’esponente
Ovviamente la precisione dipende dal numero di bit riservati alla mantissa, mentre la dimensione dai bit riservati all’esponente.
MANTISSA
00000000 01001000 10001000
ESP.
00000100
+18568
+4
• IL CALCOLO CON I NUMERI REALI È MOLTO
“PESANTE” ( A MENO CHE L’ELABORATORE
NON DISPONGA DI UNITÀ DI CALCOLO
SPECIALIZZATE: FLOATING POINT UNIT)
• LA RAPPRESENTAZIONE DEI NUMERI REALI
È SOGGETTA AD APPROSSIMAZIONI (CHE SI
PROPAGANO NELL’ESECUZIONE DI CALCOLI
SUCCESSIVI)
• LA PRECISIONE DIPENDE DAL NUMERO DI BIT
RISERVATI ALLA MANTISSA, LA DIMENSIONE
DAI BIT RISERVATI ALL’ESPONENTE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Per eseguire le operazioni aritmetiche con i numeri reali, la cui codifica è chiamata anche floating point, si usano tecniche particolari
e, a meno che l’elaboratore non disponga di “floating point unit” (o
coprocessore), il calcolo è molto “pesante”. Inoltre poiché la rappresentazione dei numeri reali è soggetta ad approssimazioni, si può
verificare che, nell’esecuzione di calcoli successivi, si possano propagare errori dovuti alla necessità di avere risultati approssimati,
con effetti disastrosi.
Un’ultima notazione per finire:
qualunque rappresentazione si utilizzi, i bit usati per rappresentare
un valore, saranno per forza un numero finito e quindi consentirà di
rappresentare solo un insieme finito di numeri, rappresentabili da un
insieme finito di cifre. In questo senso possiamo anche dire che
l’aritmetica dei calcolatori è un sottoinsieme dell’aritmetica dei numeri reali.
PAG. 2.78
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DELLE IMMAGINI
CODIFICA DELLE IMMAGINI
• L’IMMAGINE È
SUDDIVISA IN
PUNTI (PIXEL)
Dopo aver visto come si codificano il testo ed i numeri (le informazioni più tradizionali usate all’interno del computer), cercheremo ora
di capire, senza addentrarci negli aspetti puramente tecnici, con
quali modalità sono codificate le immagini.
• PIÙ PIXEL, PIÙ
RISOLUZIONE
Prendiamo come esempio l’immagine in bianco e nero di un triangolo, illustrata nella figura a fianco, e vediamo come sia possibile
rappresentarla in “modo digitale”.
I. Il primo passo consiste nel sovrapporre all'immagine una griglia
formata da righe orizzontali e verticali a distanza costante. Tutti i
quadratini, di uguale dimensione, che costituiscono la griglia vengono chiamati pixel (picture element).
CIASCUN PIXEL È
CODIFICATO COME
6
5
0
0
0
0
0
0
1
1
1
0
0
1
1
1
0
0
0
1
1
0
0
0
0
1
0
0
0
0
0
0
• COLORE
• POSIZIONE
BITMAP
“000000011000011100011110000000”
IL PROCESSO DI CODIFICA SI CHIAMA
DIGITALIZZAZIONE DELL’IMMAGINE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
II. A questo punto ogni quadratino della griglia (pixel) può essere:
• completamente bianco, se esterno all’area del triangolo
• completamente nero se interno all’area del triangolo
• in parte bianco ed in parte nero se si trova sul bordo della figura geometrica.
Assumiamo, come prima convenzione, quella di codificare con:
“1” i pixel completamente neri e quelli in cui la parte nera è
maggiore di quella bianca;
“0” i pixel completamente bianchi e quelli in cui la parte bianca
è maggiore di quella nera.
III. Ora, come seconda convenzione, consideriamo di leggere i pixel
partendo da sinistra verso destra e dall’alto verso il basso. In
questo modo otterremo una lunga sequenza di “0” e di “1” , ovvero la rappresentazione in formato digitale della nostra immagine
(vedi anche figura):
“000000011000011100011110000000”
Dopo quest'operazione, l'immagine di partenza si è trasformata in
una sorta di mappa composta di “0” e di “1”: il nome tecnico che si
usa per descrivere questa sequenza di bit è proprio BITMAP. Questo processo è anche chiamato “digitalizzazione” dell’immagine.
PAG. 2.80
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
LA “RISOLUZIONE”
“000000011000011100011110000000”
L’IMMAGINE
RIPRODOTTA È UNA
APPROSSIMAZIONE
DELLA “REALTÀ”
UN PRIMO ELEMENTO: LA ”RISOLUZIONE”
Se però proviamo a ricostruire l’immagine partendo dalla sua codifica (vedi figura a fianco), ci accorgiamo subito che il risultato è soltanto una brutta approssimazione della realtà. Il fatto è che, avendo
utilizzato una griglia con una maglia molto larga, i pixel risultanti
hanno una dimensione troppo grande: il risultato è quello di ottenere una rappresentazione della realtà molto approssimata.
Ma vediamo ora cosa accade quando aumentiamo il numero di pixel
(dimezzando il lato dei quadratini della griglia): la rappresentazione
del triangolo (v. figura a fianco), pur ancora con grosse differenze rispetto alla realtà, è già sensibilmente migliorata. Questo ci permette
di capire che più fitta sarà la griglia che sovrapponiamo all'immagine
e più la rappresentazione risulterà aderente all'originale. E in particolare, quando i pixel non saranno più riconoscibili come entità distinte,
allora probabilmente l'occhio percepirà l'immagine così com'era nella
sua forma originale.
Si usa il termine RISOLUZIONE per indicare il numero di
pixel utilizzati per la rappresentazione digitalizzata dell'immagine ovvero per indicare con quale granulosità viene effettuata la sua suddivisione in pixel.
RADDOPPIANDO IL
NUMERO DI PIXEL
MIGLIORA LA
APPROSSIMAZIONE
CON CUI È
RAPPRESENTATA
LA “REALTÀ”
LA RISOLUZIONE È CORRELATA AL NUMERO
DI PIXEL (E QUINDI ALLA LORO DIMENSIONE)
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
C’è un stretta relazione tra il numero di pixel che compongono
un’immagine e la loro grandezza. Infatti, a parità di dimensione di
un'immagine, più sono numerosi i pixel e più sono piccoli: il risultato
è una qualità più elevata dell'immagine digitale, via via più vicina all'originale. D'altra parte però, una griglia via via più fitta, significa
una maggiore numero di pixel e quindi un numero maggiore di bit
che dovranno essere utilizzati per rappresentare l'immagine stessa.
Più precisamente la “misura” della risoluzione comprende due aspetti.
1. Il primo è relativo alla quantità di punti che compongono l'immagine;
si misura indicando le righe orizzontali e verticali della griglia (ad
esempio 640 x 480, ovvero 640 pixel orizzontali X 480 verticali).
Qualche volta, in maniera equivalente, si indica il numero totale
di pixel che costituiscono l'immagine; ad esempio nel caso delle
macchine fotografiche digitali, è usuale dire che la macchina
produce foto da 1,2 megapixel (ovvero 1,2 milioni di pixel, che
equivalgono ad un’immagine da 1280 x 960 pixel).
PAG. 2.82
INFORMATICA
CAP. 2 - LA CODIFICA BINARIA DEI DATI
2. Quanto detto è relativo ad una rappresentazione interna dell'immagine ovvero ad una rappresentazione mantenuta all'interno del
computer, codificata in termini di “0” e “1”. Nel momento in cui l'immagine viene riprodotta su un dispositivo fisico (sia a video che su
carta), entra in gioco un ulteriore elemento che definisce la qualità
finale dell'immagine, così come verrà percepita. Questo ulteriore
elemento è la dimensione che assume il pixel nel momento in cui
viene impresso sul supporto fisico (schermo del video o foglio di
carta della stampante).
pixel. In termini pratici questo significa avere a disposizione una tavolozza (in inglese “palette”) composta da oltre 16 milioni di colori.
Normalmente non si misura la dimensione del singolo pixel, ma
piuttosto si indica il numero di pixel presenti in una specifica area:
di norma si indicano i punti per pollice (DPI =dot per inch);
questa ad esempio è la tipica misura utilizzata nel caso delle
stampanti (attualmente le stampanti hanno una risoluzione
che può variare tra 300-1200 DPI);
per i video poi, più comunemente si preferisce indicare il numero di punti che è in grado di visualizzare (con una terminologia
simile a quello utilizzata per definire la risoluzione dell'immagini): in questo caso si parla di una risoluzione di 800 x 600, rapportata alla dimensione fisica dello schermo (in termini di DPI la
risoluzione di un video di norma varia tra 72 e 96 DPI).
1. la risoluzione e la profondità colore forniscono, a prescindere dal
formato di stampa o di visualizzazione, una indicazione della ricchezza di dettagli complessiva dell'immagine e della sua capacità di
raffigurare la realtà;
UN SECONDO ELEMENTO: LA PROFONDITÀ COLORE
Finora abbiamo esaminato come si realizza la codifica di un’immagine
in bianco e nero (B/N). La codifica di immagini a colori (o con più tonalità di grigi) è concettualmente identica, con un unica differenza relativa al numero di bit utilizzati per codificare il singolo pixel.
Supponendo, ad esempio, di voler riconoscere 16 colori diversi, dovremmo utilizzare 4 bit per codificare le possibili 16 tonalità di colore
che ogni pixel può assumere. Se poi volessimo utilizzare 256 possibili tonalità avremmo necessità di un intero byte per la codifica del
colore. Questo significa anche che, a parità di risoluzione, la dimensione della codifica di un’immagine, cresce all’aumentare del numero di colori gestiti.
La maggior parte delle schede grafiche attuali è in grado di utilizzare
fino a 24 bit (o addirittura 32) per descrivere il colore di ogni singolo
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
RIASSUMENDO
La codifica “bitmap” è la scelta ideale per la memorizzazione di immagini
fotografiche: il numero dei pixel (RISOLUZIONE) ed il numero di colori
associato ad ogni pixel (PROFONDITÀ COLORE) sono i due elementi
fondamentali che definiscono la qualità immagine:
2. più è alta la qualità, sia sotto il profilo della risoluzione che della profondità colore, tanto più numerosi saranno i bit necessari per la rappresentazione dell'immagine stessa;
3. la risoluzione deve essere precisata al momento della creazione di
un immagine; infatti, se successivamente si decide di ingrandire
un’immagine, i pixel, mancanti verranno interpolati da quelli vicini e
per quanto possa essere “sofisticato” l'algoritmo d’interpolazione utilizzato, raramente il risultato sarà soddisfacente ma, anzi, la qualità
dell’immagine risulterà quasi sempre compromessa;
4. la dimensione dei pixel relativa al supporto su cui l'immagine viene
stampata o visualizzata, è l'ulteriore parametro che ci permette di valutare la qualità finale, così come verrà percepita dall'osservatore.
Riprendendo un concetto espresso all'inizio di questo capitolo, possiamo dire che l'immagine, ovvero un'informazione di tipo analogico, è stata rappresentata in formato digitale mediante una sequenza di campioni:
questi campioni sono i pixel.
LE TECNOLOGIE DIGITALI NELL'USO PROFESSIONALE
Una volta digitalizzata, l’immagine può essere elaborata sul computer
con specifiche tecniche digitali, ottenendo risultati impossibili da realizzare con qualunque altro sistema. Queste nuove possibilità hanno fatto
sì che l’elaborazione digitale delle immagini si sia diffusa in ambito professionale, al di fuori del mondo dell’informatica.
PAG. 2.84
INFORMATICA
CODIFICA RASTER
CAP. 2 - LA CODIFICA BINARIA DEI DATI
FORMATO DELLA CODIFICA GRAFICA (“RASTER”)
(FORMATI BMP, GIF, TIFF, JPG, PCX)
La modalità di rappresentazione di un'immagine, così come l’abbiamo descritta, viene genericamente chiamata codifica “bitmap” o
“raster”.
UN’IMMAGINE RASTER È FORMATA
DA PUNTI, DENOMINATI PIXEL,
DISPOSTI IN UNA GRIGLIA, A
OGNUNO DEI QUALI SONO
ASSOCIATE LE INFORMAZIONI
RELATIVE AL COLORE.
Un ulteriore importante aspetto, che caratterizza un'immagine “raster” è quello relativo al FORMATO con cui l'immagine stessa viene
codificata (e quindi salvata sul file). Esistono molti formati disponibili
che si caratterizzano per:
1. risoluzione massima e profondità colore che possono rappresentare;
2. possibilità o meno di comprimere i dati, con l'obiettivo di ottenere il file di dimensioni ridotte; in tal caso però certi metodi di
compressione (detti “distruttivi” o “lossy” in inglese) possono
influire negativamente sulla qualità dell'immagine, nel senso
che il minor numero di byte risultante dopo la compressione, si
paga con una minore qualità dell'immagine.
Di seguito vengono indicati i principali formati attualmente utilizzati.
AUMENTANDO IL LIVELLO DI INGRANDIMENTO
DELL’IMMAGINE, I PIXEL DIVENTANO BEN
VISIBILI.
FORMATO BMP
Il formato BMP è lo standard di Windows: viene utilizzato dal programma di gestione immagini “Paintbrush” (inserito in Windows) e
le immagini create con questo formato possono essere usate come
sfondo del desktop di Windows.
E’ LA SCELTA IDEALE PER LA MEMORIZZAZIONE
DI IMMAGINI FOTOGRAFICHE.
In funzione della risoluzione e della profondità colore, un'immagine
in formato BMP può avere una qualità elevatissima: questo comporta, di conseguenza, anche una dimensione del file molto grande,
che ne rende praticamente impossibile l'utilizzo su Internet.
LA QUALITÀ DELLE IMMAGINI RASTER È
DIPENDENTE DALLA RISOLUZIONE
UN’IMMAGINE RASTER È MOLTO SEMPLICE DA
VISUALIZZARE SUL MONITOR O DA STAMPARE
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
FORMATO GIF
il formato GIF (definito da Compuserve) può rappresentare al massimo 256 colori. Una caratteristica particolare di questo formato è
quella di permettere la realizzazioni di immagini animate (GIF animate). Il formato GIF è un formato compresso, adatto quindi per essere utilizzato sul Web. La compressione (non distruttiva) è realizzata
con il metodo LZW.
PAG. 2.86
INFORMATICA
FORMATO JPG
il formato JPG (Joint Photographic Experts Gropup) è sicuramente
uno dei formati più diffusi.
Utilizza una tecnica standard di compressione dell'immagine ideata
per comprimere immagini reali, sia a colori che in scala di grigi. Tale
tecnica di compressione permette di eliminare le informazioni non
necessarie, come ad esempio i colori che l'occhio umano non distingue. Il fatto che elimina informazioni fa sì che questo formato
venga definito “distruttivo” (“lossy”, in inglese) in quanto non mantiene le stesse informazioni cromatiche dell’immagine originaria. In
molti casi però la differenza non è riconoscibile.
CAP. 2 - LA CODIFICA BINARIA DEI DATI
Le immagini TIFF occupano molto spazio e la resa non è migliore di
un’immagine elaborata in JPG; ma, a differenza di quest'ultimo, è
un formato non distruttivo e quindi permette l'elaborazione di
un'immagine in fasi successive senza perdita di qualità (perdita che
invece si avrebbe memorizzando l'immagine in formato JPG).
FORMATO IMG
Questo formato è stato utilizzato originariamente dal programma
grafico GEM Paint. Di seguito è stato utilizzato dal programma di
impaginazione VENTURA Publisher che ne ha permesso la diffusione. I file IMG sono monocromatici o a livelli di grigio.
In generale il formato JPEG ha un rapporto di compressione che
varia da 5:1 a 15:1. La compressione viene decisa al momento di
salvare l'immagine nel formato JPEG.
Questo formato è comunemente utilizzato per le immagini sul web e
per quelle allegate ai messaggi di posta elettronica.
FORMATO TIFF
Il formato TIFF (Tagged Image File Format) è stato sviluppato dalla
Adus Corp. con l'obiettivo di farlo diventare il formato standard per
le immagini raster. Attualmente TIFF è il formato più utilizzato durante il trattamento dell'immagine:
è usato spesso per archiviare l'immagine originale e come formato di scambio fra diversi programmi di trattamento immagini,
in quanto da questo formato si può convertire in quasi tutti gli altri formati grafici;
è un formato non distruttivo;
è il formato in cui, di solito, vengono archiviate le immagini ottenute dagli scanner;
è il formato in cui conviene conservare le immagini ed i grafici
fino a che questi devono essere elaborati.
Il formato TIFF non possiede un proprio formato di compressione,
ma le immagini vengono compresse con tecniche standard come
ad esempio il metodo di compressione LZW, lo stesso usato dal
formato GIF.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.88
INFORMATICA
CODIFICA VETTORIALE
UN’IMMAGINE VETTORIALE CONSISTE IN UNA
SERIE DI ISTRUZIONI MATEMATICHE PER IL
TRACCIAMENTO DI OGNI SINGOLO ELEMENTO
CHE COMPONE L'IMMAGINE.
CAP. 2 - LA CODIFICA BINARIA DEI DATI
CODIFICA VETTORIALE
Come abbiamo visto nelle pagine precedenti, un'immagine raster è
formata da un insieme di pixel. I pixel vengono visualizzati sullo
schermo come quadratini, ma la loro dimensione è talmente minima
che normalmente l'occhio non riesce a percepire il singolo pixel.
Tuttavia se si aumenta il livello di ingrandimento dell'immagine i
pixel diventano visibili.
Questo però non è l'unico modo per rappresentare un'immagine in
un formato digitale. Una modalità di rappresentazione completamente diversa è quella che viene chiamata codifica “vettoriale”.
Un’immagine vettoriale consiste in una serie di istruzioni matematiche per il tracciamento di ogni singolo elemento che
compone l'immagine. La codifica tratta tutto come rette,
segmenti e curve. Più precisamente ogni elemento di
un’immagine vettoriale ha associate le informazioni relative
alla propria forma, alla posizione nell’immagine, ai punti iniziale e finale, alla larghezza, al colore. L’interpretazione di
questa sequenza di istruzioni produce l’effetto di “disegnare
l’immagine” sul dispositivo di output.
Tutto ciò rende adatta questo tipo di codifica per logo, caratteri e disegni al tratto.
CODIFICA ADATTA PER LOGO, CARATTERI E DISEGNI
IMMAGINI “SCALABILI”
PRIMA DELLA STAMPA IL COMPUTER PROVVEDE A
“RASTERIZZARLA”
ALCUNI FORMATI: WMF, EMF, EPS, DRW, CDR, HGL
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Le immagini in formato vettoriale sono indipendenti dalla risoluzione. Tali immagini possono essere ingrandite senza perdere i dettagli, dal momento che vengono memorizzate come insiemi di istruzioni, non come raccolte di pixel. L’immagine viene creata ogni volta
che viene visualizzata. In questo caso si dice anche che sono “scalabili” senza perdita di informazioni, sia per quanto riguarda il disegno vero e proprio che per la parte testuale.
Quando un’immagine in un formato vettoriale deve essere visualizzata sul monitor o stampata, il computer provvede a “rasterizzarla”,
ovvero a trasformarla in pixel.
Un ultimo aspetto della codifica vettoriale è relativo alla dimensione
del file: un disegno codificato in formato vettoriale ha una occupazione molto minore rispetto ad una corrispondente codifica raster.
PAG. 2.90
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
I FORMATI VETTORIALI
Anche nel caso della codifica vettoriale dell'immagine, esistono numerosi formati che sono stati definiti negli anni e che è possibile utilizzare.
In particolare, molti di questi formati che si ritengono vettoriali, consentono all’utente anche l’inclusione di dati non vettoriali, come testo o immagini rasterizzate.
Ad esempio i formati “meta” di Windows non supportano solamente
dati vettoriali. Ad esempio, un metafile di Windows può contenere
una bitmap, informazioni vettoriali e testo. La bitmap costituisce la
maggior parte dell’immagine, mentre i dati vettoriali e di testo costituiscono le annotazioni.
Di seguito vengono elencati i formati vettoriali più importanti.
• WMF
MICROSOFT WINDOWS METAFILE
• EMF
WINDOWS ENHANCED METAFILE
• DRW
MICROGRAFX DRAW
• CDR
COREL DRAW
• EPS
ENCAPSULATED POSTSCRIPT
• DXF
AUTODESK
• HGL
HEWLETT-PACKARD GRAPHICS LANGUAGE
ED I VARI FORMATI CAD
CONFRONTO RASTER – VETTORIALE
RASTER
VETTORIALE
Un’immagine raster è formata da Un'immagine vettoriale è composta
punti, denominati pixel, disposti in da una serie di istruzioni che indiuna griglia.
cano come l'immagine stessa deve
essere disegnata
Un oggetto viene rappresentato e
memorizzato come un insieme di
pixel, a ognuno dei quali sono associate le informazioni relative al
colore.
Un oggetto viene scomposto in singoli elementi grafici (segmenti, curve, ...) ognuno dei quali ha associate
le informazioni relative alla propria
forma, posizione nell'immagine, colore, dimensione, ecc.
Aumentando il livello di ingrandi- Un'immagine vettoriale può essere
mento dell’immagine, i pixel diven- ingrandita senza perdere i dettagli.
tano ben visibili.
Può avere una occupazione molto Normalmente ha una occupazione
elevata, in particolare quando si ridotta
usa una risoluzione elevata e
quando il formato non prevede la
compressione
Un’immagine raster è molto semplice da visualizzare sul monitor o
da stampare: i pixel corrispondono
ai punti del video, mentre sulla
stampante vengono convertiti in
punti d’inchiostro.
Un'immagine vettoriale, per essere
visualizzata o stampata, deve
essere
prima
convertita
in
un'immagine raster
I pixel possono essere sfumati in Questa codifica è l’ ideale per disemodo da creare bordi meno definiti gni al tratto, disegni geometrici, loe transizioni graduali tra gli oggetti. go, caratteri
Questa caratteristica rende questo
tipo di codifica la scelta ideale per
il salvataggio di immagini fotografiche.
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.92
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CODIFICA DEL SUONO
CODIFICA DEL SUONO
In questo paragrafo prendiamo in esame le tecniche utilizzate per la
rappresentazione digitale di un altro importante tipo di informazione,
quella sonora.
VOL
Ricordiamo cosa ci insegna la fisica:
“il suono si può rappresentare come un’onda sonora che descrive la variazione della pressione dell’aria nel tempo (v. la
curva rossa nella figura a fianco).
5
a1
Questa rappresentazione, di tipo analogico, descrive esattamente,
per ogni istante considerato, il valore della quantità fisica in esame.
Come sappiamo le informazioni analogiche, essendo di tipo “continuo”, non sono assolutamente gestibili sugli elaboratori digitali. Il
problema che allora si pone è quello di trovare una modalità che
permetta di passare da un’informazione di tipo analogico ad una di
tipo digitale, anche se magari approssimata.
0
t1
t
• A INTERVALLI PREFISSATI t1 SI MISURA
L’AMPIEZZA a1
• PIÙ PICCOLO È L’INTERVALLO DI CAMPIONAMENTO,
PIÙ ALTA È LA QUALITÀ DEL SUONO MEMORIZZATO
La tecnica utilizzata per la rappresentazione digitale consiste nel
misurare il valore dell’onda sonora a intervalli regolari di tempo e
nel codificare i valori rilevati in forma digitale. Questa tecnica viene
chiamata “campionamento”. Ovviamente tanto più piccolo è
l’intervallo in cui vengono campionati i valori (o maggiore sarà la
frequenza con cui si effettuano campionamenti), tanto più la rappresentazione dell’onda sarà precisa.
Anche se il tipo di informazione è completamente diverso, ancora
una volta la qualità del risultato della codifica dipende dalla numerosità dei campioni: mentre per quanto riguarda l’immagine è il numero di pixel, qui è la frequenza con cui si effettuano i campionamenti che dà la qualità del suono.
IL PROCESSO DI CODIFICA SI CHIAMA
CAMPIONAMENTO
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
----------------------------------Vale anche per i suoni quanto detto per le immagini: le possibilità offerte dalle
tecniche di elaborazione digitale dei suoni sono talmente numerose ed efficaci, che hanno portato questo tipo di tecnologia al di fuori dell’ambito della informatica.
PAG. 2.94
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
STANDARD DI CODIFICA DEL SUONO
CODIFICA WAV
FORMATO PER LA MEMORIZZAZIONE DI SEGNALI AUDIO
SECONDO LA TECNICA PCM, UTILIZZATA SUI SISTEMI
WINDOWS
QUALITÀ CD AUDIO, DIPENDENTE DALLA FREQUENZA DI
CAMPIONAMENTO DA 8 A 44 KHZ
PRODUCE FILE MOLTO GRANDI DELL’ORDINE DI 10 MBYTE
PER 1 MINUTO DI REGISTRAZIONE
CODIFICA MP3
UTILIZZA UNA TECNICA DI COMPRESSIONE CHE ELIMINA LE
INFORMAZIONI SONORE NON PERCEPITE DALL’ORECCHIO
UMANO
CON UNA QUALITÀ PRATICAMENTE PARI ALLA CODIFICA
WAV, REALIZZA UNA RIDUZIONE DEI DATI DI UN FATTORE 12
UTILIZZATA SU INTERNET
CODIFICA RM
NECESSITA DI UN LETTORE REAL AUDIO
STANDARD DI CODIFICA DEL SUONO
Con la tecnica appena vista, per codificare la voce umana (che ha
frequenze tipicamente inferiori ai 4 KHz) è necessario:
produrre 8.000 campioni al secondo, il che equivale a campionare il segnale ogni 125 milionesimi di secondo;
usare 8 bit per la codifica di ogni campione;
In definitiva, il numero di bit necessari per codificare 1 secondo di
voce umana è pari a:
8.000 campioni x 8 bit/campione = 64.000 bit ≅ 7,8 KB/sec
La codifica della musica, con una qualità pari a quella dei normali CD,
richiede un numero di byte molto superiore. Infatti per la musica di
qualità è necessario:
utilizzare due registrazioni distinte, una per il canale destro e
l’altra per il canale sinistro (corrispondenti a due microfoni);
produrre 44.100 campioni al secondo,
usare 16 bit per ogni campione.
Anche in questo caso è possibile calcolare il numero di bit necessari per codificare 1 secondo di musica:
2 x 44.100 campioni x 16 bit/camp. = 1.411.200 bit = 172,2 KB/sec
MOLTO COMPRESSO, UTILIZZZATO IN STREAMING
CODIFICA MIDI
NON SI CODIFICA IL SUONO MA LE ISTRUZIONI (NOTE
MUSICALI) PER GENERARLO
Questi semplici calcoli mostrano come cresce il numero di bit necessari per la memorizzazione del suono al crescere della “qualità”
cui si rappresenta l'informazione sonora.
PUÒ ESSERE UTILIZZATO PER CONTROLLARE DA
COMPUTER STRUMENTI MUSICALI DOTATI DI INTERFACCIA
DIGITALE
USATO PER I GIOCHI, SUL WEB E PER LE SUONERIE DEI
TELEFONI CELLULARI
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.96
INFORMATICA
CAP. 2 - LA CODIFICA BINARIA DEI DATI
IL FORMATO REAL AUDIO
LA CODIFICA STANDARD DI WINDOWS: .WAV
Sui sistemi Windows, per la memorizzazione dei segnali audio, viene utilizzata una tecnica definita PCM. I file corrispondenti, che utilizzano questo formato per la memorizzazione del suono, hanno l'estensione .WAV.
Utilizzando questo sistema di codifica, la qualità dipende dalla frequenza di campionamento e dal numero di bit utilizzati per ogni
campione. Con una adeguata frequenza di campionamento si può
ottenere un'ottima qualità audio, tant'è che questo è il formato utilizzato nei classici CD audio per la memorizzazione dei brani musicali.
Il limite di questa codifica consiste nei file molto grandi che produce,
dell'ordine di:
circa 0,5 MB per un minuto di voce registrata;
circa 10 MB per un minuto di musica registrata in qualità CD.
Questo fatto rende inutilizzabile questo tipo di codifica sul Web.
UN FORMATO COMPRESSO: MP3
Utilizzando l'algoritmo denominato “MP34” è possibile “comprimere”
un file audio di tipo .WAV:
con una perdita di qualità praticamente inavvertibile all'orecchio
umano;
ma realizzando una riduzione dei dati pari a circa un fattore 12.
I file “musicali” compressi con questa tecnica hanno come estensione “.MP3” e vengono genericamente chiamati “file mp3”. Questo
formato compresso, riducendo l’occupazione di un file sonoro di un
ordine di grandezza, ha avuto una grandissima diffusione e ha reso
possibile lo scambio di brani musicali attraverso Internet.
4
Un altro formato compresso, molto utilizzato per trasmettere audio
attraverso il Web, è il formato Real Audio. I file che utilizzano questo formato si riconoscono dalla estensione “.RM”.
Per il loro ascolto è necessario disporre di un particolare programma, il “lettore Real Audio” , liberamente scaricabile Internet. Un file
RM ha dimensioni più ridotte rispetto ai file WAV e MP3, ma anche
la qualità audio è sensibilmente inferiore.
Tipicamente i file Real Audio si ascoltano via Web, in modalità “streaming”, ovvero con la riproduzione della musica che inizia e continua
mano a mano che il computer riceve i dati dalla rete, senza la necessità di doverli scaricare sul disco fisso del proprio computer.
IL FORMATO MIDI
Il formato MIDI rappresenta un modo completamente diverso di codificare i suoni. Infatti a differenza dei formati appena visti, un file
MIDI non contiene al suo interno il suono degli strumenti, bensì le
note che devono essere eseguite.
In altre parole è come se, all'interno del file, ci fossero codificate le istruzioni per il dispositivo di output (ad es. la scheda audio). Elaborando queste istruzioni, il dispositivo riesce a riprodurre le note richieste, con una timbrica simile a quella degli strumenti musicali definiti nelle stesse istruzioni. Il limite è che permette la sola riproduzione di suoni generati con strumenti (in altre parole non è possibile
codificare la voce).
Questo modo di codificare il suono permette al file MIDI di avere una
grandissima compattezza: ogni singolo evento MIDI (che può essere pensato equivalente a una nota) occupa soltanto undici byte e un
intero brano musicale occupa mediamente qualche decina di KB.
Questo fatto ha reso i file MIDI molto utilizzati per la realizzazione
delle colonne sonore all'interno delle pagine Web, nei giochi e per le
suonerie dei telefonini.
(MPEG-LAYER 3, una variante dell'algoritmo MPEG)
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.98
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
CONFRONTO MIDI E WAV CON CODIFICA GRAFICA
CONFRONTO TRA LE DIVERSE CODIFICHE
Un interessante confronto può essere fatto tra i formati utilizzati per la
codifica delle immagini e i formati utilizzati per la codifica dei suoni.
CODIFICA DELLE
IMMAGINI
DIFFERENZE TRA FORMATO MIDI E WAVE
Codifiche
Raster
BMP
GIF
JPEG
TIFF
MIDI
IN UN FILE MIDI CI
SONO SOLO COMANDI
WAVE
IN UN FILES WAVE
CI SONO SUONI
SE FACCIAMO UN PARALLELO CON LA
CODIFICA DELLE IMMAGINI
CODIFICA
VETTORIALE
CODIFICA
RASTER
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Codifiche
Vettoriali
WMF
EMF
DRW
EPS
DXF
CONFRONTO
Una prima categoria di formati, ha l'obiettivo di codificare l'informazione, sia grafica che sonora, attraverso il processo di
digitalizzazione. In altre parole, le tecniche che appartengono questa prima categoria elaborano l'informazione analogica
(corrispondente ad un'immagine o a un
suono) trasformandola in una informazione digitalizzata.
Appartengono a questa prima categoria
tutte le codifiche “raster” e le codifiche
WAV, MP3 e RM nel caso dei suoni.
Questa seconda categoria approccia il
problema della rappresentazione dell'informazione, sia visiva che sonora, da un
punto di vista diametralmente opposto.
Invece di partire dall’informazione analogica e dallo studio dei metodi per la sua
scomposizione in “campioni” che possano
essere poi tradotti in un formato digitale, si
pone l'obiettivo di identificare le opportune
“istruzioni” con cui pilotare specifici dispositivi di output, in modo tale che si possa
generare l'informazione di partenza. Ad
esempio, invece di procedere con il campionamento del suono e con la memorizzazione dei relativi campioni, si cerca di
identificare le istruzioni (note) con cui pilotare una scheda audio, in modo tale che
riproduca il brano musicale di partenza.
Appartengono a questa seconda categoria le codifiche vettoriali (per la grafica) e
la codifica MIDI (per i suoni).
CODIFICA DEI
SUONI
WAV
MP3
RM
MIDI
PAG. 2.100
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
MA COSA CONTIENE UN BYTE IN MEMORIA?
MA ALLORA COSA RAPPRESENTA QUEL BYTE IN MEMORIA?
Giunti al termine di questo capitolo, verifichiamo il livello di comprensione raggiunto dal lettore, relativamente alla codifica binaria
dell’informazione, con una domanda :
00110001
“Il byte “00110001”, che supponiamo sia presente in
qualche parte nella memoria del nostro sistema, cosa
rappresenta ?”
UN NUMERO INTERO
IN CODIFICA BINARIA
UN NUMERO INTERO
IN CODIFICA BCD
UN NUMERO REALE
IN FLOATING POINT
UN CARATTERE IN
CODIFICA ASCII
La risposta dovrebbe ormai essere nota: il byte, in quanto codifica
binaria di un dato (o di una sua parte) può rappresentare molteplici
tipi di informazione. Tra le altre potrebbe essere:
•
•
•
•
•
•
•
•
un numero intero codificato in binario
un numero intero codificato in BCD
un numero intero codificato in ASCII
una parte della codifica un numero reale in floating point;
un carattere in formato ASCII
una parte della codifica di un‘immagine
una parte della codifica di un suono
e altro ancora.
Da non dimenticare poi che in memoria ci sono anche i programmi
e che quel byte potrebbe anche rappresentare la codifica di una istruzione del programma.
“ Ma allora come si fa a capire che cosa rappresenta ?”
CODIFICA DI UN
IMMAGINE
Il byte (come tutti i dati) di per se stesso non ha alcun significato. Acquista significato soltanto nel momento in cui lo interpretiamo in funzione della “realtà che rappresenta”.
CODIFICA DI UN
SUONO
Sotto questo punto di vista possiamo anche dire che la domanda
iniziale era stata posta male e che, per poter avere una risposta,
andrebbe riformulata, per esempio, in questi termini:
MA ANCHE LE
ISTRUZIONI DI UN
PROGRAMMA
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
“Sapendo che quel byte rappresenta un carattere codificato in codice ASCII, quale carattere rappresenta ?”
PAG. 2.102
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
APPENDICE 1
GLI OPERATORI LOGICI
GLI OPERATORI LOGICI
OPERATORE NOT
L’OPERAZIONE NOT INVERTE IL SEGNO.
A
0
1
NOT A
1
0
OPERATORE OR
IL RISULTATO È VERO QUANDO ALMENO
UNO DEI DUE OPERANDI È VERO
A
0
0
1
1
B
0
1
0
1
A OR B
0
1
1
1
OPERAZIONE AND
IL RISULTATO È VERO SOLO SE TUTTI
E DUE GLI OPERANDI SONO VERI
A
0
0
1
1
B
0
1
0
1
A AND B
0
0
0
1
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
Gli operatori logici sono stati definiti nell’ambito di un formalismo
detto Algebra di Boole. Questa algebra si basa sull’applicazione di
tre operazioni logiche (dette anche operazioni booleane) a operandi
che possono assumere due soli valori: vero o falso.
Se ipotizziamo di codificare con 1 il valore vero, e con 0 il valore
falso, possiamo adeguatamente rappresentare un operando di una
espressione booleana con un bit.
I tre operatori elementari, previsti all’interno dell’Algebra di Boole (e
chiamati anche operatori booleani), sono:
NOT, OR, AND
Il funzionamento dei tre operatori è definito da quelle che si chiamano tavole di verità.
A
0
1
NOT A
1
0
L’operazione NOT si applica a 1 operando.
L’operazione NOT inverte il segno.
A
0
0
1
1
B
0
1
0
1
A OR B
0
1
1
1
L’operazione OR si applica a 2 operandi.
L’operazione OR dà come risultato vero
se almeno uno dei due operandi è vero
A
0
0
1
1
B
0
1
0
1
A AND B
0
0
0
1
L’operazione AND si applica a 2 operandi.
L’operazione AND dà come risultato vero
solo se tutti e due gli operandi sono veri
PAG. 2.104
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
ESPRESSIONI BOOLEANE
Proprietà associativa
(A OR B) OR C = A OR (B OR C)
(A AND B) AND C = A AND (B AND C)
ESPRESSIONI BOOLEANE
Applicando le tre operazioni booleane a diversi operandi si possono
costruire espressioni logiche (o booleane) di varia complessità.
La valutazione di una espressione logica consiste nella valutazione
del valore (0,1) dell’espressione, in funzione del valore degli operandi. In altri termini si tratta di creare una tavola della verità
dell’espressione.
Riportiamo alcune delle principali proprietà degli operatori booleani.
Proprietà associativa
Proprietà commutativa
A AND B = B AND A
A OR B = B OR A
(A AND B) AND C = A AND (B AND C)
(A OR B) OR C = A OR (B OR C)
Proprietà commutativa
A AND B = B AND A
A OR B = B OR A
Proprietà di idempotenza
A AND A = A
A OR A = A
Proprietà di idempotenza
A AND A = A
A OR A = A
Leggi di Morgan
Leggi di Morgan
NOT (A AND B) = (NOT A) OR (NOT B)
NOT (A OR B) = (NOT A) AND (NOT B)
NOT (A AND B) = (NOT A) OR (NOT B)
NOT (A OR B) = (NOT A) AND (NOT B)
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.106
CAP. 2 - LA CODIFICA BINARIA DEI DATI
INFORMATICA
LE PROPOSIZIONI
LE PROPOSIZIONI
Una particolare forma assunta dagli operandi sono le proposizioni,
di cui ne vediamo alcuni esempi. Per un concorso, i candidati devono possedere i seguenti requisiti:
A. devono avere un’età maggiore o uguale a 21 anni
B. e (un’età) minore di 46 anni
ESEMPIO:
PER UN CONCORSO, I CANDIDATI
POSSEDERE I SEGUENTI REQUISITI:
A. DEVONO AVERE UN’ETÀ MAGGIORE
O UGUALE A 21 ANNI
B. E (UN’ETÀ) MINORE DI 46 ANNI
DEVONO
PER QUANTO RIGUARDA IL TITOLO DI STUDIO,
DOVRANNO AVERE
C. UNA LAUREA IN INGEGNERIA
D. O (UNA LAUREA) IN FISICA
(A AND B) AND (C OR D)
Per quanto riguarda il titolo di studio,
C. dovranno avere una laurea in ingegneria
D. o (una laurea) in fisica
In questo esempio abbiamo individuato 4 proposizioni, chiamate per
brevità A, B, C, D. L’espressione booleana che rende il significato
del testo è la seguente:
(A AND B) AND (C OR D)
Valutiamo l’espressione calcolando la sua tavola della verità.
A
B
C
D
espress
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
1
Il risultato =1 (vero) si ha quando A e B sono entrambe vere e
quando C oppure D oppure tutte e due sono vere
NESSUNA PARTE DI QUESTO TESTO PUÒ ESSERE RIPRODOTTA SENZA LA PREVENTIVA AUTORIZZAZIONE DELL’AUTORE
PAG. 2.108