DERIVATE E LORO APPLICAZIONE
SIMONE ALGHISI
1. Applicazione del calcolo differenziale1
Abbiamo visto a lezione che esiste un’importante legame tra la continuità di una funzione y =
f (x) in un punto x0 ∈ dom (f ) e la drivabilità della stessa funzione in x0 .
(1.1) Teorema Se una funzione f : D → R definita in un dominio D ammette derivata in
x0 ∈ D, allora f è anche continua in x0 .
Abbiamo anche osservato che la derivata di una funzione y = f (x) in un punto x0 rappresenta
il coefficiente angolare della retta tangente t al grafico della funzione nel suo punto di ascissa x0 ,
cioè
mt = f 0 (x0 ) .
L’anno scorso (in Goniometria) è stato dimostrato che il coefficiente angolare di una retta coincide
con la tangente trigonometrica dell’angolo α che la retta forma con il semiasse positivo delle ascisse,
cioè m = tg α. Da quanto detto precedentemente possiamo affermare che
mt = f 0 (x0 ) = tg α .
Riportiamo per comodità una tabella in cui sono riassunte le derivate delle funzioni più importanti.
f (x)
x ∈ dom (f )
f 0 (x)
xn con n ∈ N \ {0}
x∈R
nxn−1
α
x con α ∈ R \ {0}
x≥0
αxα−1
x
e
x∈R
ex
ax
x∈R
ax ln a
cos x
x∈R
− sen x
sen x
x∈R
cos x
π
2
tg x
x 6= 2 + kπ 1 + tg x = cos12 x
ln x
x>0
1/x
−1/2
arcsin x
−1 ≤ x ≤ 1
1 − x2
−1/2
arccos x
−1 ≤ x ≤ 1 − 1 − x2
arctg x
x∈R
(1 + x2 )−1
c∈R
x∈R
0
|x|
x 6= 0
x/|x|
x ∈ dom (f 0 )
x∈R
x≥0
x∈R
x∈R
x∈R
x∈R
x
1
/Z
π − 2 ∈
x ∈]0, +∞[
−1 ≤ x ≤ 1
−1 ≤ x ≤ 1
x∈R
x∈R
x 6= 0
Ricordiamo inoltre alcune regole di derivazione principali.
Somma e differenza Se f, g : D → R sono due funzioni derivabili in D, allora anche la
somma e la differenza f ± g è derivabile in D e risulta
D[f (x) ± g(x)] = f 0 (x) ± g 0 (x) ,
∀x ∈ D ;
(1)Queste note sono state scritte anche grazie all’aiuto della Prof.ssa I. Scalvini del Liceo Scientifico Calini di
Brescia.
1
Prodotto Se f, g : D → R sono due funzioni derivabili in D, allora anche il prodotto f · g è
derivabile in D e risulta
D[f (x) · g(x)] = f 0 (x)g(x) + f (x)g 0 (x) ,
∀x ∈ D ;
Quoziente Se f, g : D → R sono due funzioni derivabili in D con g(x) 6= 0 in D, allora anche
il quoziente f /g è derivabile in D e risulta
D[f (x)/g(x)] =
f 0 (x)g(x) − f (x)g 0 (x)
,
[g(x)]2
∀x ∈ D ,
g(x) 6= 0 ;
Composizione Se g : D → R è derivabile in x0 ∈ D e f : g(D) → R è derivabile in g(x0 ),
allora la funzione composta f ◦ g è derivabile in x0 e si ha
D[f (g(x0 ))] = f 0 (g(x0 )) · g 0 (x0 ) .
Vediamo alcuni problemi che possono essere risolti mediante l’ausilio delle derivate.
2. Primo problema
Il primo problema che dobbiamo affrontare è il seguente: date la funzione y = f (x) e l’ascissa
x0 del punto di tangenza, determinare l’equazione della retta tangente.
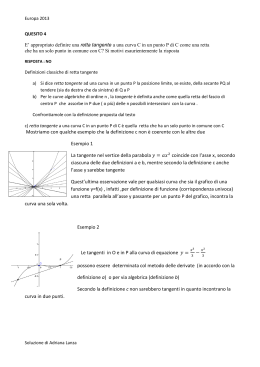
(2.1) Esempio Determinare la retta tangente t al grafico della curva f (x) = x2 + x − 5 (parabola)
nel suo punto di ascissa x0 = 4.
Soluzione. Per risolvere il problema proposto è sufficiente:
(1) calcolare l’ordinata del punto di tangenza y0 = f (x0 ) = f (4) = 15, quindi P (4; 15);
(2) calcolare la funzione derivata: f 0 (x) = 2x + 1;
(3) calcolare il coefficiente angolare mt = f 0 (x0 ) = f 0 (4) = 9.
L’equazione della retta richiesta è
y − y0 = m(x − x0 )
⇒
y − 15 = f 0 (4)(x − 4)
⇒
y − 15 = 9(x − 4) ,
da cui
t:
y = 9x − 21 .
♣
(2.2) Esempio Determinare l’equazione cartesiana della retta tangente t alla curva la cui espressione analitica è f (x) = 5 sen x + 1 nel punto x0 = 0.
Soluzione. Procedendo come nell’Esempio (2.1) si ha P (0; 1), f 0 (x) = 5 cos x e quindi mt = f 0 (0) =
5. Segue che la retta tangente richiesta ha equazione cartesiana
t:
y − 1 = 5(x − 0) ⇒ y = 5x + 1 .
♣
(2.3) Esempio Determinare l’equazione della retta tangente alla funzione f (x) = ln2 x nel suo
punto di ascissa x0 = e.
Soluzione. Osservando che dom (f ) =]0; +∞[ e che x0 ∈ dom (f ), è lecito richiedere la retta
tangente al grafico della funzione nel suo punto x0 = e. Anzitutto f (e) = 1, da cui P (e; 1). Inoltre
2 ln x
f 0 (x) =
.
x
Il coefficiente angolare della retta tangente vale mt = f 0 (e) = 2/e. Segue che la retta tangente t ha
equazione cartesiana y = 2e x − 1. ♣
x
(2.4) Esempio Determinare l’equazione delle retta tangente t alla curva f (x) = xe 1−x nel punto
x0 = 2.
Soluzione. Come visto nei precedenti esempi, determiniamo l’ordinata del punto di tangenza y0 =
f (2) = 2e−2 = 2/e2 . Calcolando la derivata della funzione si ottiene:
x
x
f 0 (x) = e 1−x + xe 1−x
x
1 − x − x(−1)
x2 − x + 1
1−x ·
=
e
.
(1 − x)2
(1 − x)2
Il coefficiente angolare della retta richiesta vale mt = f 0 (2) = 3/e2 . L’equazione cartesiana della
retta tangente è
4
3
t : y = 2x − 2 .
e
e
♣
(2.5) Esempio Data la cubica di equazione f (x) = hx3 +3kx, determinare i parametri h, k ∈ R in
modo tale che la funzione data sia tangente nel punto P (3; 3) alla parabola (con asse di simmetria
verticale), di vertice V (1; 1).
Soluzione. Anzitutto, la parabola è della forma y = ax2 + bx + c (con a 6= 0). Come di consueto,
per determinare i coefficienti della parabola imponiamo il passaggio per P , per V e utilizziamo
b
l’ascissa del vertice (xV = − 2a
):

b



 − 2a = 1 ,
a + b + c = 1,



 9a + 3b + c = 3 .
Risolvendo il sistema si ottengono le soluzioni a = 12 , b = −1 e c = 23 , pertanto la parabola ha
equazione cartesiana y = g(x) = 12 x2 − x + 23 .
Per determinare i parametri h e k imponiamo il passaggio della cubica per P (3; 3), ottenendo
27h + 9k = 3 cioè 9h + 3k = 1. Il testo del problema afferma che la cubica è tangente alla
parabola in P . Ciò significa che le due curve possiedono la stessa retta tangente t passante per P .
Ricordando il legame tra coefficiente angolare della retta tangente t e la derivata della funzione, si
ha mt = f 0 (xP ). Derivando la cubica e la parabola, calcolando le corrispondenti derivate nel punto
xP = 3 e imponendo che tali valori siano uguali otteniamo:
f 0 (x) = 3hx2 + 3k ,
g 0 (x) = x − 1
da cui
f 0 (xP ) = f 0 (3) = 27h + 3k ,
g 0 (xP ) = g 0 (3) = 2 ⇒ 27h + 3k = 2 .
Risolvendo il sistema in cui compaiono l’ultima relazione trovata e il passaggio della cubica per P
si ha
(
27h + 3k = 2 ,
9h + 3k = 1 ,
la cui (unica) soluzione è h =
1
18
e k = 16 . La funzione richiesta è quindi f (x) =
1 3
18 x
(2.6) Esempio Si consideri la famiglia Fk di curve di equazione y = f (x), dove
1
f (x) = x3 − (k + 2)x2 − (k + 7)x − 3 .
3
+ 21 x. ♣
Determinate per quali valori del parametro k ∈ R le curve corrispondenti hanno punti nei quali la
tangente è perpendicolare alla retta r di equazione cartesiana 3x − 5y + 6 = 0.
Soluzione. La retta r, in forma esplicita, ha equazione y = 35 x + 65 . Si deduce che il coefficiente
angolare della retta r è mr = 35 . La retta tangente alla curva deve essere ortogonale alla retta r,
quindi dovrà possedere coefficiente angolare m0 = − m1r , cioè m0 = − 53 . Segue che
1
m0 = f 0 (x) = 3x2 − 2(k + 2)x − (k + 7) .
3
5
0
Ponendo m = − 3 , si ottiene l’equazione di secondo grado
1
5
3x2 − 2x(k + 2) − (k + 7) = − ⇒ 9x2 − 6x(k + 2) − 2 − k = 0 .
3
3
Tale equazione ammette due soluzioni reali se, e solo se, il discriminante è positivo, cioè ∆ ≥ 0.
Calcolando il discriminante dell’equazione e risolvendo la disequazione ∆ ≥ 0, si ottengono i valori
del parametro k ammissibili: k ≤ −3 ∪ k ≥ −2. ♣
3. Secondo Problema
Il secondo problema che ci poniamo è il seguente: dati la funzione y = f (x) ed il coefficiente
angolare m della retta tangente t, determinare l’ascissa del punto di tangenza x0 .
(3.1) Esempio Determinare le coordinate dei punti nei quali la retta tangente al grafico della
funzione f (x) = x3 + 2x + 3 ha coefficiente angolare m = 5.
Soluzione. Indichiamo con x0 l’ascissa (incognita) del punto generico di tangenza. Per rispondere
al quesito è sufficiente:
(1) calcolare la funzione derivata: f 0 (x) = 3x2 + 2;
(2) calcolare mt in funzione dell’incognita x0 : mt = 3x20 + 2;
(3) risolvere l’equazione mt = 5, cioè 3x20 + 2 = 5.
Risolvendo l’equazione si ottengono due soluzioni: x0 = ±1. Le coordinate dei punti di tangenza
sono:
T1 (1; f (1)) ⇒ T1 (1; 6) ,
T2 (−1; f (−1))
⇒
T2 (−1; 0) .
♣
(3.2) Esempio Determinare le coordinate dei punti nei quali la retta tangente al grafico della
funzione f : R → R definita da
p
f (x) = 1 − x2
ha coefficiente angolare m = 2.
Soluzione. Il dominio della funzione data è dom (f ) = [−1; 1]. Calcolando la derivata della funzione
si ha
1
x
f 0 (x) = √
· (−2x) = − √
.
2 1 − x2
1 − x2
Si osservi che il dominio della funzione è dom (f 0 ) =] − 1; 1[ e che esso è un sottoinsieme del dominio
della funzione data. Calcolando ora il coefficiente angolare della retta tangente t in funzione della
derivata si ha
x0
mt = − p
.
1 − x20
Risolvendo infine l’equazione mt = 2 si ottiene
x0
=2
−p
1 − x20
da cui
⇒
q
−x0 = 2 1 − x20
(
(
⇒
x0 ≤ 0 ,
x20 = 4 − 4x20 ,
x0 ≤ 0 ,
x20 =
4
5
.
√
√
Il sistema ammette come unica soluzione x0 = − √25 . Il punto richiesto è quindi T (−2/ 5; f (−2/ 5)),
√
√
cioè T (−2/ 5; 1/ 5). ♣
(3.3) Esempio Determinare i punti in cui la retta tangente alla curva di equazione f (x) =
è parallela alla retta passante per i punti A(−2; 6) e B(−1; 4).
x+2
x
Soluzione. Il coefficiente angolare della retta r passante per i punti A e B è
yA − yB
6−4
mAB =
=
= −2 .
xA − xB
−2 − (−1)
Calcolando la derivata della funzione data, si ottiene
2
x − (x + 2)
=− 2.
f 0 (x) =
x2
x
Il coefficiente angolare della retta tangente t nel generico punto della curva di ascissa x0 è
2
mt = f 0 (x0 ) = − 2 .
x0
Risolvendo l’equazione mt = −2, si ha x0 = ±1. Pertanto, i punti richiesti hanno sono P (1; 3) e
Q(−1; −1). ♣
(3.4) Esempio Si consideri la funzione f : R → R definita da
3
f (x) = ex− 2 tg x · tg x .
Determinare i punti per i quali risulta f 0 (x) = 0 (si ricorda che i punti per i quali la derivata è
nulla si dicono punti stazionari).
Soluzione. Il dominio della funzione y = f (x) data è l’insieme
n
o
π
Df = x ∈ R : x 6= + kπ, k ∈ Z .
2
Calcolando la derivata della funzione, si ha
x− 3 tg x
3
3
x−
tg
x
2
0
2
f (x) = 1 + tg x · e 2
+ tg x · e 2
1−
1 + tg x =
2
1 3 2
3 3
1
2
x− 32 tg x
2
x− 23 tg x
1 + tg x + tg x − − tg x
=e
− tg x + tg x − tg x + 1 .
=e
2 2
2
2
Ora è sufficiente risolvere l’equazione f 0 (x0 ) = 0. Ricordando che la funzione esponenziale è sempre
positiva e mai nulla, l’equazione che dobbiamo quindi risolvere è
3
1
− tg3 x0 + tg2 x0 − tg x0 + 1 = 0 ,
2
2
cioè
3 tg3 x0 − 2 tg2 x0 + tg x0 − 2 = 0 .
Ponendo t = tg x0 si ha 3t3 −2t2 +t−2 = 0. Chiamando il primo membro p(t), si nota che p(1) = 0.
Mediante la regola di Ruffini, il polinomio lo si può scomporre nel modo seguente:
p(t) = (t − 1) 3t2 + t + 2 .
Il trinomio racchiuso nelle parentesi tonde possiede il discriminante ∆ < 0, quindi non possiede
zeri. L’unica soluzione dell’equazione è quindi t = 1, cioè tg x0 = 1. Segue che x0 = π4 + kπ, con
k ∈ Z.
In conclusione abbiamo trovato infiniti punti stazionari xk aventi per ascissa π4 + kπ con k ∈ Z. ♣
(3.5) Osservazione I punti le cui ascisse annullano la derivata di una funzione y = f (x), oltre
ad essere chiamati punti stazionari, sono anche detti punti a tangente orizzontale. Infatti,
ricordando il legame che intercorre tra derivata f 0 (x0 ) e coefficiente angolare della retta tangente
nel punto della curva di ascissa x0 , se f 0 (x0 ) = 0 allora il coefficiente angolare della tangente mt
deve essere nullo. Una retta avente mt = 0 è parallela all’asse delle ascisse.
4. Terzo problema
Il terzo problema consiste nel determinare l’angolo formato da due curve.
(4.1) Definizione Chiamiamo angolo formato da due curve di equazioni y = f (x) e y = g(x)
in un punto P (x0 ; y0 ) ad esse comune l’angolo acuto formato dalle tangenti a queste curve nel punto
P.
Se l’angolo sopra citato risulta essere retto, diremo che le due curve sono ortogonali. Si può
verificare che l’angolo acuto α che è formato da due rette incidenti aventi coefficienti angolari m1
e m2 è
m1 − m2 .
tg α = 1 + m1 m2 Se tali rette sono tangenti alle due curve y = f (x) e y = g(x) rispettivamente, possiamo affermare
che i coefficienti angolari coincidono con il valore delle corrispondenti derivate calcolate nel punto
x0 (ascissa del punto di intersezione tra le due curve):
0
f (x0 ) − g 0 (x0 ) .
(4.2)
tg α = 1 + f 0 (x0 )g 0 (x0 ) (4.3) Esempio Determinare l’angolo formato dalle due curve γ1 e γ2 di espressione analitica
rispettivamente f (x) = 4x2 − 4x e g(x) = 1 − x2 nel loro punto di intersezione di ordinata nulla.
Soluzione. Anzitutto cerchiamo di trovare i punti comuni alle due curve γ1 e γ2 (parabole):
(
y = 4x2 − 4x ,
γ1 ∩ γ2 =
y = 1 − x2 .
Risolvendo il sistema si ottengono i punti P (1; 0) e Q(−1/5; 24/25). Il punto che dobbiamo prendere
in considerazione è P . Per risolvere il quesito proposto dobbiamo:
(1) calcolare le funzioni derivate delle due funzioni: f 0 (x) = 8x − 4 e g 0 (x) = −2x;
(2) calcolare i coefficienti angolari delle due rette tangenti: m1 = f 0 (1) = 4 e m2 = g 0 (1) = −2.
Note queste informazioni possiamo concludere l’esercizio ricavando la tangente dell’angolo (acuto)
formato dalle due rette mediante la relazione (4.2):
4 + 2 6
= ,
tg α = 1 − 8 7
da cui α = arctg 67 . ♣
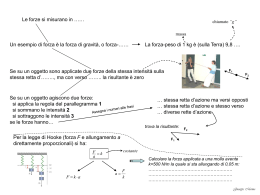
(4.4) Esempio La parabola P1 di equazione y = ax2 + bx + c (a 6= 0) interseca la parabola P2
di equazione y = 1 − x2 nel punto A di ascissa nulla e nel punto B di ascissa 2. Si determini
l’equazione di P1 sapendo che l’angolo formato dalle due parabole nel punto B è α = arctg 12 .
Soluzione. Per iniziare, determiniamo le coordinate di A e di B. Poichè A, B ∈ P2 , si ha yA = 1 e
yB = −3. Imponiamo ora il passaggio della parabola P1 per i punti A e B:
(
(
passaggio di P1 per A ,
c = 1,
→
passaggio di P1 per B ,
4a + 2b + c = −3 .
Risolvendo il piccolo sistema precedente si ha c = 1 e b = −2a − 2. La parabola P1 assume la
forma y = f (x) = ax2 − (2a + 2)x + 1. Indicando con g(x) la seconda parabola e procedendo come
nell’esercizio precedente, calcoliamo le derivate delle due funzioni (parabole):
f 0 (x) = 2ax − 2a − 2 ,
g 0 (x) = −2x .
Per determinare i coefficienti angolari delle rette tangenti alle due parabole in B è necessario
calcolare f 0 (xB ) e g 0 (xB ) ottenendo:
f 0 (xB ) = 2a − 2 ,
g 0 (xB ) = −4 .
Applicando la relazione (4.2) si ha
1 2a + 2 1
2a + 2
1
= =
=± .
⇒
tg arctg
2
2
9 − 8a
9 − 8a
2
5
Risolvendo le due equazioni ammettono le seguenti soluzioni: a = 12
e a = 13
4 . Sostituendo tali
valori nel sistema precedente si ottengono due parabole. La retta marrone è la tangente in B alla
parabola P2 .
y
y=
13 2
4 x
−
17
2 x
+1
A(0;1)
x
O
y=
B(2;−3)
P2
y = −4x
+5
♣
5 2
12 x
−
17
6 x
+1
(4.5) Esempio Si considerino le seguenti funzioni:
f (x) = x2 + x − 1 ,
g(x) = x2 + k
k ∈ R.
Determinare per quali valori di k le tangenti alle due curve nei loro punti di intersezione formano
un angolo di π/4.
Soluzione. Per individuare i punti di intersezione tra le due curve è sufficiente risolvere il seguente
sistema
(
y = x2 + x − 1 ,
y = x2 + k ,
ottenendo come unica soluzione P k + 1; k 2 + 3k + 1 . Le derivate delle due funzioni sono rispettivamente
f 0 (x) = m1 (x) = 2x + 1 ,
g 0 (x) = m2 (x) = 2x .
Calcolando il valore delle due derivate nel punto xP = k + 1, si ottengono i coefficienti angolari
delle due rette tangenti alle curve nel punto P comune:
m1 = 2k + 3 ,
m2 = 2k + 2 .
π
4
Ricordando inoltre che tg = 1, si ha
m1 − m2 = 1 ⇒ 2k + 3 − 2k − 2 = 1 ,
1 + m1 m2 1 + (2k + 2)(2k + 3) da cui |1 + (2k + 2)(2k + 3)| = 1. Risolvendo le due equazioni
1 + (2k + 2)(2k + 3) = −1 ,
1 + (2k + 2)(2k + 3) = 1
si ottengono le soluzioni k = −1 oppure k = − 23 . ♣
x
.
x−2
Determinare le equazioni delle rette tangenti alle curve nel loro punto di ascissa x0 = 0. Calcolare
inoltre la tangente goniometrica dell’angolo che le tangenti formano.
(4.6) Esempio Si considerino le curve di equazioni rispettivamente f (x) = x2 −x e g(x) =
Soluzione. Anzitutto notiamo che dom (f ) = R e dom (g) = R \ {2}, quindi è lecito considerare il
punto di ascissa x0 = 0. Notando che f (0) = g(0) = 0, si ha che il punto di tangenza è P (0; 0).
Calcolando le derivate delle due funzioni si ha
2
f 0 (x) = 2x − 1 ,
g 0 (x) = −
,
(x − 2)2
da cui i coefficienti angolari delle rette tangenti alle due funzioni f e g sono, rispettivamente,
m = f 0 (0) = −1 e m0 = g 0 (0) = − 12 . La retta tangente ad f in P ha equazione cartesiana
y − 0 = m(x − 0), cioè y = −x (bisettrice del II e del IV quadrante). La retta tangente alla funzione
g ha equazione y − 0 = m0 (x − 0), cioè y = − 21 x.
La tangente goniometrica dell’angolo formato dalle due rette tangenti è
1
−1 + 12
tg α = = .
1 + (−1) − 12 3
♣
(4.7) Esempio Determinare l’equazione cartesiana della parabola P con asse di simmetria parallelo all’asse delle ordinate sapendo che P è tangente alla parabola y = x2 nel punto si ascissa 1 e
passa per A(3; 4). Trovare inoltre i punti Q della parabola tali che la somma delle loro coordinate
sia α ∈ R.
Soluzione. La parabola richiesta è della forma y = ax2 + bx + c con a 6= 0. Sapendo che essa
è tangente alla parabola y = x2 nel punto di ascissa x0 = 1 si ricava che il punto di tangenza è
T (1; 1). Il coefficiente angolare della retta tangente è data dalla derivata di y = x2 calcolata nel
punto x0 = 1, quindi m = 2. L’equazione della retta tangente t è quindi y − 1 = m(x − 1), cioè
y = 2x − 1. Per determinare i coefficienti della parabola imponiamo anzitutto il passaggio per A e
per T ottenendo
(
9a + 3b + c = 4 ,
a + b + c = 1,
6a−1
da cui y = ax2 + 3−8a
2 x + 2 , con a da determinare. Se ora y = f (x) è l’equazione della parabola
che stiamo cercando, si ha f 0 (1) = m = 2, essendo
f 0 (x) = 2ax +
3 − 8a
2
f 0 (1) = 2a +
e quindi
3 − 8a
.
2
Imponendo ora f 0 (1) = 2 si ottiene a = − 14 . La parabola richiesta è quindi y = − 14 x2 + 52 x − 54 .
y
y = 2x − 1
T (1;1)
x
y = − 14 x2 + 52 x −
O
Il punto Q richiesto è della forma Q x; − 41 x2 + 52 x −
si ha
5
4
5
4
, con x ∈ R. Imponendo che xQ + yQ = α,
x2 − 14x + 4α + 5 = 0 .
Ponendo y = x2 − 14x e y = −4α − 5, il problema si riduce alla discussione del seguente sistema
parametrico misto:

2
parabola passante per l’origine O ,

 y = x − 14x
y = −4α − 5
fascio improprio di rette orizzontali ,


−∞ < x < +∞ intervallo di esistenza della x ,
La situazione è riportata nel grafico sottostante.
y
y = x2 − 14x
x
O
y = −4α − 5
α = 11
La retta passante per il vertice V della parabola ha equazione y = xV , cioè y = −49. Il valore di α
corrispondente alla retta del fascio passante per il vertice della parabola lo si ottiene imponendo il
passaggio della retta y = −4α − 5 per il vertice V (7; −49) della parabola y = x2 − 14x. Si ottiene
α = 11. La generica retta del fascio intersecherà la parabola in du punti quando α ≤ 11 (si noti
che il fascio decresce verso l’alto). ♣
Esercizi
1. Determinare la derivata della funzione
f (x) = x ln3 x − 3x ln2 x + 6x ln x − 6x .
Successivamente, calcolare le ascisse dei punti del grafico della funzione y = f (x) nei quali la retta
tangente ha coefficiente angolare m = 8.
[f 0 (x) = ln3 x. Si ha un unico punto di ascissa x0 = e2 .]
√
2. Date le funzioni f (x) = x + 1, g(x) = x3 e h(x) = sen x, determinare la funzione composta
A(x) = (f ◦ g ◦ h)(x) e calcolare la derivata A0 (x).
√
3. Determinare le ascisse dei punti della parabola di equazione cartesiana y = −x2 + 4x 3 nei
quali la tangente risulti inclinata di π4 o di π3 rispetto al semiasse positivo delle ascisse.
[x1 =
√
4 3−1
;
2
x2 =
√
2 3
3 .]
x
4. Date le curva di equazioni f (x) = x − 2 ln x e g(x) = ln xe2 , determinare l’angolo acuto formato
dalle tangenti ad esse nel loro punto di intersezione.
2+e
[α = arctg 3e−4
.]
5. Determinare per quali valori del parametro reale k la famiglia di parabole Pk di equazione
y = (1 − k)x2 + 3kx − 7 + k le tangenti alla corrispondente parabola nei punti di ascissa 2 e 13
4
risultano ortogonali tra loro.
[k = 2 oppure k = 27
7 .]
√
6. Date le curve di equazioni cartesiane f (x) = 1 − x e g(x) = x2 + 23 x − 52 , determinare gli angoli
acuti formati dalle tangenti ad esse nei loro punti di intersezione.
[α = arctg 27 ; β = arctg 2.]
√
7. Scrivere l’equazione della retta tangente alla curva di equazione cartesiana f (x) = 5x2 − 1 nel
suo punto di ascissa x0 = −1.
[y = − 52 x − 21 .]
8. Scrivere l’equazione della retta tangente alla curva di equazione cartesiana f (x) = 3 cos2 x −
2 sen x + 5x nel suo punto di ascissa x0 = 0.
[3x − y + 3 = 0.]
√
9. Si consideri la funzione f (x) = e x . Dopo aver determinato il dominio Df della funzione data,
determinare l’equazione della retta t tangente al grafico della funzione y = f (x) passante per P (1; e).
[Il dominio è Df = [0; +∞[. La retta t ha equazione ex − 2y + e = 0.]