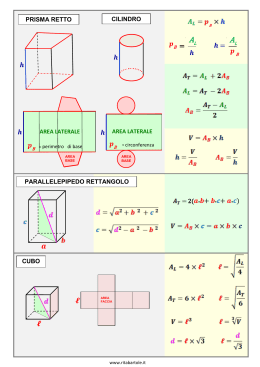
geometria solida
Prismi e Piramidi: aree e volumi
prisma retto
1
2
3
4
5
6
Calcolare l’area totale di un prisma avente come base un triangolo rettangolo
con i cateti uguali a 3 e 4 ed altezza uguale a 0,5
Calcolare l’area laterale di un prisma a base esagonale avente lo spigolo di
base uguale a 15 e l’altezza uguale alla sua terza parte
Calcolare il volume di un prisma a base pentagonale avente l’area di base
uguale a 3,5 ed altezza uguale allo spigolo di un cubo avente la stessa area di
base
Calcolare l’area laterale e quella totale di un prisma quadrangolare regolare
alto 6,4 e avente il perimetro di base uguale a 2,4
Calcolare l’area laterale e quella totale di un prisma retto avente come base
un trapezio isoscele e altezza uguale a 5. Le basi del trapezio misurano
rispettivamente 20 e 38 e la sua altezza è uguale al doppio della base minore
Calcolare l’area laterale di un prisma obliquo avente come base un triangolo
equilatero di lato uguale a 6 e di area totale uguale a 36
parallelepipedo rettangolo
7
8
9
10
11
Calcolare la superficie laterale del parallelepipedo rettangolo che ha un lato
lungo 10 cm, l’altro 8 cm e l’altezza uguale a 3 cm
Calcolare la superficie laterale del parallelepipedo rettangolo che ha un lato
lungo 6, l’altro i del precedente e l’altezza uguale a 1
Calcolare l’area totale del parallelepipedo rettangolo avente l’area di base
uguale a 20 e le dimensioni nel rapporto 2:5. L’altezza di tale figura è uguale
alla differenza tra le dimensioni di base
Calcolare il volume di un parallelepipedo rettangolo la cui diagonale è uguale
a 15 , il perimetro di base è uguale a 7 e le due dimensioni differiscono di 3
Le tre dimensioni di un parallelepipedo rettangolo sono 2,3,5. Calcolare
l’area totale, il volume e l’area di base
cubo
12
13
14
15
16
v 1.0
Un cubo ha l’area totale uguale a 18. Calcolare la sua diagonale
Calcolare la superficie totale di un cubo avente la diagonale uguale a 72
Calcolare l’area di base di un cubo che ha le dimensioni uguale all’altezza del
parallelepipedo rettangolo di volume 16 e area di base doppia rispetto a
quella del cubo
Il volume di un cubo è 729. Qual è la sua area totale?
Calcolare il peso in grammi di un cubo di marmo di peso specifico
e area di base uguale a
© 2013 - www.matematika.it
1 di 3
geometria solida
17
18
19
20
21
22
23
24
25
26
27
28
v 1.0
Prismi e Piramidi: aree e volumi
piramide
Nel triangolo rettangolo ABC il triplo del cateto AB è uguale al quadruplo del
cateto AC e l’ipotenusa BC misura
. Determinare il volume e l’area della
superficie laterale della piramide di vertice V, base ABC e altezza VC sapendo
che i triangoli ABC e BCV sono isoperimetri.
(Si considera: V B = 90°)
Nel triangolo ABC la bisettrice dell’angolo C interseca AB nel punto D che
dista
da A e
da B. Sapendo che BC =
, determinare l’area
della superficie totale della piramide retta la cui base è ABC e la cui altezza
misura
Il lato del triangolo equilatero ABC misura
. Il punto P divide un’altezza
in due parti di cui quella contenente il vertice è la metà dell’altra. Calcolare
l’area della superficie laterale della piramide di vertice V, base ABC e altezza
VP =
Nel trapezio isoscele ABCD la base maggiore AB, la base minore e il lato
obliquo misurano rispettivamente
. Detto M il punto medio di
AB, determinare l’area delle superfici laterali delle piramidi rette aventi per
base i triangoli AMD e BCD e altezza per entrambe
270 a2 378 a2
Calcolare l’area di base e il volume di una piramide avente per base un
rettangolo di dimensioni 15 e 25 ed altezza uguale a 30
Nel triangolo rettangolo ABC l’ipotenusa AC supera il cateto BC di
. Nella
piramide di base ABC, vertice V e altezza VC, lo spigolo VA supera lo spigolo
VB di
. Sapendo che VB è il triplo di B determinare il volume della
piramide VABC
Una piramide ha per base un triangolo i cui lati misurano
,
,
.
Determinare gli spigoli laterali sapendo che ciascun lato della base è uguale
alla semisomma dei due spigoli laterali uscenti dai suoi estremi
Una piramide triangolare regolare ha l’altezza di
e lo spigolo di base
. Determinare l’area della superficie laterale della piramide ed il
raggio della sfera in essa inscritta
Una piramide regolare quadrangolare di vertice V, altezza VO ed apotema
VM, ha l’area della superficie laterale di
. Sapendo che
, determinare la misura dell’altezza della piramide
Una piramide di vertice V ed altezza VH ha per base un triangolo ABC
rettangolo in A. Sapendo che
ed
, determinare il volume della piramide
Una piramide di vertice V ha per base un triangolo ABC rettangolo in B e per
altezza
. Sapendo che
e
, determinare l’area della superficie totale della piramide
Una piramide di vertice V ha per base un triangolo ABC rettangolo in B e per
altezza
. Sapendo che
e
, determinare l’area della superficie totale della piramide
© 2013 - www.matematika.it
2 di 3
geometria solida
Prismi e Piramidi: aree e volumi
tronco di piramide
29
30
31
32
33
34
35
36
37
38
39
v 1.0
Un tronco di piramide regolare quadrangolare ha l’altezza, l’apotema e la
superficie laterale rispettivamente di
e 480
.
Determinare la diagonale del tronco ed il raggio della sfera ad esso
circoscritta
Un tronco di piramide regolare quadrangolare ha le diagonali delle basi e lo
spigolo laterale rispettivamente di
e 14
. Determinare
l’area della superficie laterale del tronco ed il raggio della sfera ad esso
circoscritta
Nel triangolo rettangolo ABC, i cateti AB e BC misurano rispettivamente
e
. Condotto per C il segmento
perpendicolare al piano
del triangolo, determinare:
a) la distanza BH del vertice B dallo spigolo VA
b) l’area della superficie laterale del tronco che si ottiene sezionando la
piramide VABC con il piano condotto per H parallelamente alla base ABC
Un tronco di piramide regolare quadrangolare ha l’area della superficie
laterale di
e le facce laterali inclinate di 45° sul piano della base
maggiore. Determinare l’altezza del tronco ed il raggio della sfera ad esso
circoscritta, sapendo che il lato della base maggiore misura 7
2
Un tronco di piramide a base quadrata di apotema
ed altezza
,
ha il lato della base maggiore lungo
. Calcolare volume e superficie
totale
Una piramide retta a base quadrata ha l'altezza
e l'apotema è i 13/12
dell'altezza. Determinare il volume della piramide e quella del tronco che si
ottiene tagliando la piramide con un piano parallelo alla base e distante
dalla base
Un tronco di piramide a base quadrata ha il lato della base maggiore lungo
. Sapendo che il lato della base minore è 2/5 di e che il volume è di
, trovarne l’ altezza
Un tronco di piramide triangolare regolare ha un volume di
.
Sapendo che la base maggiore ha altezza di 5
, e che il lato della base
minore è 2/7 del lato della base maggiore, trovarne l’ altezza
Un tronco di piramide a base quadrata ha il lato della base maggiore
uguale a
e quello della base minore uguale a
di . Sapendo che
l’apotema misura
, calcolare l’area della superficie laterale
Un tronco di piramide regolare a base qualsiasi ha superficie laterale
Sapendo che i perimetri delle basi sono in rapporto 3/2 e che la loro somma
misura
, calcolare l’apotema
Un tronco di piramide a base quadrata ha
e =7/5 di . Sapendo
che la superficie laterale misura 48
cm2, calcolarne il volume
© 2013 - www.matematika.it
3 di 3