LA COMPRESSIONE
Dispensa per il Corso di
Tecnologie Informatiche
di Chiara Epifanio
Attenzione: si tratta di una copia preliminare, la copia definitiva
verrà messa quanto prima online.
Indice
1 La compressione
2 Algoritmi elementari di codifica
2.1 Eliminazione di ripetizioni . . .
2.2 Codifica differenziale . . . . . .
2.3 Rappresentazione topografica .
2.4 Codifica a blocchi . . . . . . . .
1
.
.
.
.
9
9
10
11
12
3 Compressione statistica, o probabilistica
3.1 Algoritmo di Huffman . . . . . . . . . . . . . . . . . . . . . .
3.2 Codifica di Shannon-Fano . . . . . . . . . . . . . . . . . . . .
3.3 Codici aritmetici . . . . . . . . . . . . . . . . . . . . . . . . .
12
12
17
20
4 I compressori linguistici
4.1 LZ77: una compressione sliding window .
4.2 Problemi derivanti dall’uso di LZ77 . . .
4.3 LZ78: un nuovo algoritmo . . . . . . . .
4.4 LZW . . . . . . . . . . . . . . . . . . . .
22
23
25
27
35
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
La compressione
Principale obiettivo di questa breve dispensa è quello di approfondire nozioni
e tecniche legate alla problematica della compressione dati.
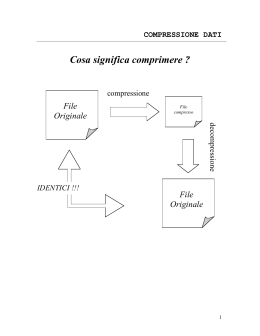
Da un punto di vista intuitivo “comprimere” un testo, un’immagine, un
suono o più in generale un oggetto significa ridurne le dimensioni. Lo scopo
della compressione è, quindi, quello di fornire una rappresentazione dei dati
in una forma ridotta senza che il significato degli stessi venga cambiato. In
tal modo sarà possibile ricostruire in un momento successivo i dati originali
o una loro approssimazione. Diamo adesso due definizioni utili per potere
approfondire meglio questo nuovo concetto.
Definizione 1.1 : Si definisce Lossy data compression un qualsiasi algoritmo che permetta di ottenere, tramite la decodifica della codifica dell’input,
non i dati iniziali, bensı̀ una loro approssimazione.
Definizione 1.2 : Si definisce Lossless data compression un qualsiasi algoritmo che permetta di ottenere, tramite la decodifica della codifica dell’input,
esattamente i dati iniziali.
Gli algoritmi di cui alla definizione 1.1 sono utili in casi nei quali non sia
necessario riottenere esattamente l’input dato, ma ne basta una ricostruzione
abbastanza fedele. Un esempio si può avere nel caso della compressione di
immagini, in cui basta ottenere, tramite decodifica, un’immagine che differisca dall’input in qualche pixel, in modo che l’occhio umano non si possa
accorgere della differenza.
Gli algoritmi di cui alla definizione 1.2, invece, sono più appropriati per
comprimere testi (in una qualsiasi lingua o codice), casi in cui, quindi, non è
1
consentito perdere neanche un bit dell’informazione di partenza. Nonostante
ciò, esistono alcuni algoritmi lossless utilizzati per comprimere immagini.
Supponendo che l’alfabeto sorgente sia A e che il codominio della nostra
funzione sia 2 = {0, 1} (considerando le codifiche all’interno di un qualsiasi
altro alfabeto otterremmo gli stessi risultati) e chiamando A∗ l’insieme di
tutte le stringhe ottenute, tramite concatenazione, a partire da elementi di
A, diamo la seguente definizione.
Definizione 1.3 : Si definisce compressore, o compressione, una qualsiasi funzione parziale α : A∗ → 2∗ (la “parzialità” è richiesta per poter
raggiungere coefficienti di compressione migliori, dal momento che il compressore può cosı̀ tralasciare parole che, per il nostro scopo, sono inessenziali). Se α è una funzione iniettiva, allora l’algoritmo dato sarà lossless.
Infatti, in tal caso l’operazione di codifica sarà tale che in fase di decodifica
si avrà un’unica ricostruzione dell’input, quella originale.
Assumeremo d’ora in poi di considerare solo “lossless data compression”.
Per far ciò sarà necessario, come detto, che la compressione sia una funzione
iniettiva.
Alla fine degli anni ’40, i primi anni della teoria dell’informazione, ci
si cominciò a porre il problema di creare nuovi algoritmi di codifica che
si basassero sui concetti di ridondanza e di quantità di informazione. Ci
si rese conto che, conoscendo le probabilità dei simboli di un testo qualsiasi, sarebbe stato possibile limitare la quantità di memoria necessaria per
lo stesso. I primi algoritmi effettivi di compressione dati sono stati introdotti
nel 1950 e sono quelli di Shannon-Fano e di Huffman, che verranno esaminati nel prossimo paragrafo, che si basavano proprio su concetti statistici. In quegli anni, però, non ci si poteva avvalere certamente di processori
2
molto efficienti, per cui, ad una attenta analisi, il rapporto costi-benefici tra
i costi computazionali per i processi di codifica e di decodifica ed i benefici ottenuti per far ciò non risultava molto conveniente. Con l’avvento di
microprocessori economici, invece, la compressione ha assunto un ruolo più
rilevante ed è diventata una componente essenziale nel campo della teoria
dell’informazione e nello studio delle sue applicazioni all’immagazzinamento
di dati e alla trasmissione. Questi sono, infatti, i campi in cui viene maggiormente sfruttato l’uso di compressori. Esaminiamo brevemente la situazione
in entrambi i casi.
Per quanto riguarda l’immagazzinamento dei dati, essi vengono compressi
prima di essere archiviati in un supporto di memoria in modo che esso possa
contenere il più possibile dei dati, che poi verranno decompressi all’atto della
lettura.
USER
ENCODER
STORAGE
DEVICE
DECODER
USER
Nonostante l’esistenza ormai sul mercato di supporti di memorizzazione
capaci di contenere al loro interno una gran quantità di dati, gli algoritmi
di compressione mantengono la loro notevole importanza: per esempio sono
molto interessanti per la creazione di archivi o, anche, per l’applicazione a
tipi particolari di dati, quali le immagini.
Per quanto riguarda la trasmissione, invece, sarà necessario che colui che
trasmette i dati li comprima prima di farlo e che chi li riceve li decomprima
prima di leggerli.
3
SENDER
DECODER
ENCODER
RECEIVER
Trasmissione
Per esempio, consideriamo un’azienda che abbia 20 linee telefoniche dedicate che collegano Palermo con Roma e che trasmetta, attraverso queste
linee, dati grazie a dei modem. Se i dati possono essere compressi di un
fattore 2, cioè viene impiegata la metà dei bits necessari per trasmettere
l’input per intero, allora la velocità con cui verranno trasmessi viene raddoppiata (indipendentemente dalla velocità dei modems). L’azienda potrà,
dunque, decidere se inviare e ricevere il doppio dei dati ogni giorno, ovvero
se mantenere solo 10 linee telefoniche dedicate.
La codifica consiste nella trasformazione di un insieme di simboli emessi
da una sorgente in un nuovo insieme che passa poi per un canale di trasmissione. All’uscita dal canale, l’insieme di simboli viene trasformato mediante
un decoder, che permette al receiver di ottenere l’input dato. Il canale può
essere un supporto fisico, una linea telefonica o altro. Durante la codifica e
la decodifica, un insieme può dovere soddisfare certe proprietà, o vincoli, e
può subire alcune alterazioni (in questo caso l’insieme verrà modificato e si
dirà che è un “canale con rumore”, o “noisy channel”).
Il processo di codifica-decodifica dovrà rispondere alle esigenze di chi lo
applica, cioè alle prestazioni richieste dall’applicazione specifica. Nel nostro
caso, cioè la compressione, lo scopo sarà ovviamente quello di ridurre la dimensione dell’informazione trasmessa o immagazzinata. Vi sono altri casi di
processi di codifica-decodifica: ad esempio quando parliamo di crittografia lo
scopo primo è che i dati codificati siano accessibili solo alle persone autorizzate. Il codice correttore di errori, invece, cercherà di “correggere gli errori”
apportati da un noisy channel ad un insieme dato. In altri casi, l’insieme
verrà modificato in modo da potere soddisfare a certi vincoli che riguardano
4
la suddivisione dei simboli dell’insieme che dovrà passare per il canale. Tutti
questi generi di codifica appena esaminati possono essere racchiusi in un unico
schema (cf. fig. seguente), in cui l’ordine con il quale si presentano i vari
processi di codifica è essenziale. Per esempio la decodifica di compressione,
come d’altronde anche quella di crittografia, dovrà avere a che fare solo con
canali senza rumore.
Definizione 1.4 : Definiamo Canale senza rumore un canale che non
“sporchi” il segnale emesso (colui che riceve i dati ottiene esattamente quelli
trasmessi, senza alcuna “sbavatura”).
CANALE SENZA RUMORE
CANALE CON RUMORE
SOURCE
ENCODER
COMPRESSIONE
ENCODER
CORRETTORE
DI ERRORI
ENCODER
CHANNEL
VINCOLI
RUMORE
DECODER
DECODER
DECODER
VINCOLI
CORRETTORE
DI ERRORI
COMPRESSIONE
D’ora in poi considereremo solo canali senza rumore, in modo da ottenere
risultati che dipendano esclusivamente dall’algoritmo di compressione adoperato. Questa assunzione non costituirà una limitazione dal momento che,
come abbiamo detto, grazie ai codici correttori di errori potremo sempre
ottenere canali senza rumore o buone approssimazioni di essi.
5
RECEIVER
Definizione 1.5 : Diciamo che il nostro algoritmo di compressione-decompressione lavora in tempo reale se esiste una costante k tale che in ogni k
unità di tempo esattamente un nuovo carattere viene letto dall’encoder e uno
viene scritto dal decoder. L’unica eccezione a ciò è che noi possiamo avere un
certo ritardo tra l’encoder e il decoder. Quindi, esiste un’altra costante l tale
che durante le prime l unità di tempo il decoder può non produrre caratteri
e, nel caso in cui l’input sia finito, possono trascorrere l unità di tempo tra
quando l’encoder ha finito di leggere e quando il decoder ha finito di restituire
caratteri.
Definizione 1.6 : Definiamo on-line un algoritmo che lavora man mano
che riceve i dati, off-line, invece, uno che esamina tutti i dati prima di
produrre l’output.
Se gli algoritmi considerati sono on-line, allora l’immagazzinamento di
dati può essere visto come un caso particolare di trasmissione, caso in cui
il sender ed il receiver coincidono. E’ da notare, comunque, che algoritmi
on-line lavorano anche off-line, ma non vale il viceversa.
Adesso dobbiamo però stabilire come valutare se un algoritmo di compressione è “buono”, e quindi avere dei criteri su cui basarci per scegliere se
in un dato caso è più conveniente adoperare un tipo di codifica o un altro.
Per far ciò diamo la seguente definizione.
Definizione 1.7 : Dato un compressore α : A∗ → 2∗ definiamo coefficiente di compressione della parola w ∈ A∗
τ (w) =
6
|w|
|α(w)|
In generale, risulterà ovviamente che |α(w)| < |w| e che, quindi, τ (w) >
1 . È ovvio, inoltre, in base a quanto detto ed alle definizioni date, che
un alto coefficiente di compressione rappresenta una codifica più efficiente.
Secondo l’input da comprimere, possono, infatti, esistere compressori più o
meno adatti. Possono esistere, però, anche input per i quali un compressore
produca un output più voluminoso!
Osservazione 1.1 Alcuni testi presentano il coefficiente di compressione
come
|α(w)|
.
|w|
Seguendo una tale definizione, ovviamente, le codifiche più efficienti avranno
coefficienti di compressione più bassi.
Un’altra grandezza molto importante è l’entropia di una sorgente. Esistono due tipi fondamentali di entropia: l’entropia statistica e l’entropia
topologica di una sorgente. Nella teoria dell’informazione - e in rapporto alla
teoria dei segnali - l’entropia misura la quantità di incertezza o informazione
presente in un segnale aleatorio. Da un altro punto di vista l’entropia è la
minima complessità descrittiva di una variabile aleatoria, ovvero il limite inferiore della compressione dei dati. Essa rappresenta un lower bound sulla
possibile compressione lossless: il minore numero di bit necessari per codificare un messaggio.
Si deve a Claude Shannon lo studio dell’entropia in tale contesto. Nel
primo teorema di Shannon, o teorema di Shannon sulla codifica di sorgente,
egli dimostrò che una sorgente casuale d’informazione non può essere rappresentata con un numero di bit inferiore alla sua entropia, cioè alla sua
autoinformazione media.
L’entropia di una variabile aleatoria X è la media dell’autoinformazione
I(xi ) delle realizzazioni della variabile stessa (x1 , x2 , . . . , xn ):
7
H(X) = E [I (xi )] =
n
X
I(xi ) · P (xi ) =
i=1
n
X
P (xi ) · log2
i=1
1
.
P (xi )
La base del logaritmo originariamente utilizzata da Shannon fu quella
naturale, tuttavia è oggi di uso comune la base 2 in quanto consente di
ottenere dei risultati più chiari (in particolare, il valore di entropia ottenuta
è misurato in bit). Si nota molto facilmente che H(X) ≥ 0.
L’entropia di una sorgente binaria con probabilità p ed 1 − p è:
1
1
+ (1 − p) log2
.
p
1−p
Vale quindi 1 bit in caso di equiprobabilità dei risultati, e 0 bit nel caso
in cui la sorgente sia completamente prevedibile (e cioè emetta sempre zeri o
sempre uni). Tale risultato è ragionevole in quanto nel primo caso si afferma
che è necessario un bit d’informazione per ogni messaggio emesso dalla sorgente, mentre nel secondo caso non è necessario alcun bit in quanto si conosce
a priori il valore di tutti i messaggi e quindi la sorgente è del tutto inutile.
Si dimostra che per l’entropia vale sempre la relazione:
H(X) = p log2
H(X) ≤ log2 n.
dove n la cardinalità dell’alfabeto di messaggi considerati (nel caso della
moneta, n = 2).
In analoga maniera si può parlare di entropia topologica di una sorgente,
concetto sul quale non ci dilungheremo, ma che ha la seguente definizione.
Definizione 1.8 Si definisce entropia topologica della sorgente X la
quantità
H(X) = lim sup
n→∞
8
1
log(sn )
n
dove sn = |X ∩ An |, essendo An l’insieme delle stringhe di lunghezza n
sull’alfabeto A (per convenzione assumiamo che log(0) = 0).
Descriviamo adesso alcuni particolari algoritmi di compressione dati.
2
Algoritmi elementari di codifica
Esaminiamo adesso alcuni algoritmi elementari di codifica che possono essere
utili ai fini della compressione dati.
2.1
Eliminazione di ripetizioni
Supponiamo di avere un testo s ad elementi in A che contenga un certo numero di ripetizioni di caratteri. All’interno di esso sostituiamo ogni sequenza
di n lettere α con
&αn
dove & è un nuovo carattere, che ovviamente verrà omesso nel caso in cui
|A| = 1, che sta ad indicare il fatto che la lettera che lo segue è ripetuta. In
termini matematici ciò corrisponde a scrivere αn .
Questo algoritmo è molto utile in quanto vengono eliminate molte ridondanze e quindi viene risparmiato spazio superfluo. Non sarà conveniente
se la stringa considerata contiene poche ripetizioni, dal momento che occuperemmo 3 unità di memoria (&αn, una per ogni simbolo), ottenendo un
output più lungo dell’input dato. In questo caso, quindi, non si potrebbe
certo parlare di compressione.
9
2.2
Codifica differenziale
La codifica differenziale viene adoperata comunemente per creare archivi di
successive versioni di uno stesso file. Il file iniziale viene interamente memorizzato sul disco e per ogni versione successiva vengono registrate solo le
differenze con le precedenti.
Supponiamo di avere una sequenza (u1 , u2 , ..., un ) di dati, essa può essere
rappresentata dalla sequenza di differenze (u1 , u2 − u1 , ..., un − un−1 ) dove “-”
deve essere un’operazione appropriata.
Un esempio può essere quello della memorizzazione di successive foto di
uno stesso panorama. Lo spostamento delle foglie causato dal vento potrebbe
essere l’unica differenza tra due di esse. Sarebbe, pertanto, inutile memorizzare in entrambi i file tutti i particolari delle foto, lo si potrebbe fare solo in
uno di essi e nel secondo conservare le informazioni riguardo la differenza tra
i due panorami.
Un altro esempio di codifica differenziale può essere dato dall’esame delle
righe di una pagina. Una prima codifica viene effettuata sulle righe consecutive: se la codifica binaria della n-esima di esse è
0111001 0101101 1010101 1010100 1010110 1010000
e quella della (n + 1)-esima è
0101001 0101101 0111010 1101010 1101110 0001000
la riga che deve essere trasmessa sarà
0010000 0000000 1101111 0111110 0111000 1011000.
10
Se in quest’ultima le sequenze di “1” vengono codificate tramite la loro
posizione e la loro lunghezza all’interno della riga, otteniamo:
(3, 1), (12, 2), (2, 4), (2, 5), (3, 3), (4, 1), (2, 2)...
(il che significa che al 3◦ posto c’è un 1, successivamente dal 12◦ posto in poi
ci sono due 1 successivi, ...). Pagine con righe diverse tra di loro porteranno,
ovviamente, a coefficienti di compressione molto bassi; i migliori coefficienti
verranno raggiunti nel caso di pagine interamente bianche (o nere).
2.3
Rappresentazione topografica
Un altro algoritmo elementare è la rappresentazione topografica. A tal fine
si utilizza uno sfondo uniforme e si codificano le posizioni di alcuni caratteri
predominanti nel testo e diversi dal carattere che riempie lo sfondo. Assumiamo, ad esempio, che ad ogni carattere venga associata la sua codifica
ASCII e che lo sfondo sia composto da “-” (cioè 00101101), allora la sequenza
“ − e − e − −ee”,
cioè
00101101 01100101 00101101 01100101 00101101 00101101 01100101 01100101
viene trasformata in
01010011 01100101,
il che corrisponde a “Se” nel codice ASCII. La stringa 01010011 (“S”) determina la posizione della “e” all’interno dell’input dato, infatti troviamo un
“1” nella posizione di ogni carattere diverso da “-”; in tal modo sarà molto
semplice la decodifica.
11
2.4
Codifica a blocchi
Gli algoritmi più comuni per comprimere un testo sfruttano la codifica di
ogni simbolo in esso presente tramite una stringa di lunghezza dlogk (n)e (in
cui n rappresenta la cardinalità dell’insieme sorgente e k quella del nuovo
alfabeto). Questo algoritmo viene denominato “codifica a blocchi k-aria”.
Un esempio si ha nel caso del codice ASCII, che trasforma ognuno dei 256
caratteri ASCII in una stringa binaria costituita da 8 cifre successive facenti
parte dell’alfabeto {0, 1}; questo è, ovviamente, un esempio di codifica binaria
a blocchi.
3
Compressione statistica, o probabilistica
Agli algoritmi di codifica presentati nella sezione precedente si affiancano
nella letteratura classica due grosse classi di compressori: gli algoritmi statistici si basano sulla probabilità dei singoli simboli dell’input di presentarsi
all’interno dello stesso per poterlo comprimere; quelli linguistici, invece, comprimono una sequenza sostituendo al suo interno sottosequenze della stessa
con puntatori a strutture dati chiamate dizionari. La ricerca nel campo della
compressione sta facendo, però, notevoli passi avanti, il che ha portato a
nuovi tipi di algoritmi di compressione dati, tra i quali quelli che fanno uso
di “antidizionari”. In questa sezione approfondiremo gli algoritmi statistici.
3.1
Algoritmo di Huffman
La Codifica di Huffman è un algoritmo greedy (un algoritmo greedy permette
di ottenere una soluzione ottima di un problema prendendo in ogni punto
di scelta dell’algoritmo la decisione che, al momento, appare la migliore localmente ottima) di codifica usato per la compressione lossless di dati. Il
12
suo inventore è David A. Huffman, che la presentò nell’articolo A Method
for the Construction of Minimum-Redundancy Codes, pubblicato nel 1952.
Nel 1951 a David Huffman, ai tempi dottorando in Teoria dell’Informazione
al Massachusetts Institute of Technology (MIT), fu assegnata da Robert M.
Fano una tesi sul problema di trovare il codice binario più efficiente per
rappresentare una sorgente probabilistica. A Huffman venne l’idea di usare
un albero binario ordinato in base alle frequenze dei singoli simboli emessi
dalla sorgente e cosı̀ inventò un nuovo algoritmo di codifica che creava un
codice a lunghezza variabile.
Supponiamo di avere una stringa w ad elementi in un alfabeto Σ e di
esaminarla carattere per carattere (o equivalentemente una sorgente probabilistica che emette simboli ognuno con una certa probabilità). Immaginiamo, inoltre, di conoscere per ogni carattere si di w la probabilità che esso
compaia nella stringa w. Il criterio su cui si basa questo algoritmo è che
ai simboli più probabili vengono associate le parole più brevi (foglie meno
profonde nell’albero che verrà in seguito descritto) e a quelli meno probabili
quelle più lunghe (foglie più profonde). Dunque, le codifiche ottenute avranno
lunghezza variabile, esattamente ognuna di esse richiederà un numero intero
di bits. Cosı̀ facendo, la lunghezza del testo codificato sarà ridotta al minimo
e il codice ottenuto sarà prefisso, il che permetterà di ottenere la decodifica
esatta (dal momento che nessuna codifica può essere prefisso di nessun’altra).
Ad ogni carattere si dell’input w sull’alfabeto Σ viene associata una parola
Huff(si ) (dove con Huff abbiamo indicato la funzione di codifica), sull’alfabeto
{0, 1}, del codice prefisso da determinare. Se riscriviamo le parole Huff(si ) su
un albero binario A, le foglie sono in corrispondenza biunivoca con le lettere.
13
Definizione 3.1 : Se nx è il numero di occorrenze del simbolo x all’interno
di w (informazione che ci fornisce la probabilità che esso si presenti all’interno
del testo), definiamo peso di A, la
X
nx d(fx )
dove d(fx ) rappresenta la distanza dalla radice della foglia associata alla lettera x.
Il nostro scopo è, dunque, quello di determinare, dato un testo w, l’albero
A di peso minimo.
Algoritmo di Huffman (costruzione dell’albero di peso minimo)
In tale algoritmo ricopre un ruolo fondamentale l’insieme
N = {(wi , pi )/wi ∈ Σ∗ }
di coppie costituite da sottostringhe di w e pesi delle sottostringhe. Analizziamo, dunque, l’algoritmo
1. Inizializziamo N = {(si , nsi )/si ∈ Σ, si ∈ w} con le lettere di w e i
relativi numeri di occorrenze in w e ordiniamo i suoi elementi in ordine
decrescente secondo i pesi/occorrenze;
2. Ripetiamo iterativamente fino a che la cardinalità di N non diventi 1
le seguenti operazioni:
• consideriamo i due elementi di N di peso minimo e attribuiamo
ai nodi corrispondenti uno stesso padre il cui peso sarà la somma
di quelli dei nodi dati;
• eliminiamo da N i due nodi del punto precedente e inseriamo un
elemento rappresentante il padre (di peso la somma dei due pesi
degli elementi eliminati) .
14
Dal momento che esiste la possibilità, dato un nodo, di scegliere arbitrariamente le codifiche dei suoi figli (0 al sinistro e 1 al destro o viceversa) e, a
parità di peso, quale altro nodo scegliere per renderlo suo fratello, la codifica
non sarà unica.
Esempio: Sia w = abracadabra. Le occorrenze delle lettere sono: na =
5, nb = 2, nc = 1, nd = 1, nr = 2. Un albero creato dall’algoritmo è
RADICE
0
1
5
6
0
5
1
2
4
0
5
2
1
2
2
0
5
a
2
b
1
2
1
1
r
c
d
15
Le parole di {0, 1}∗ associate alle lettere a, b, c, d, r sono, dunque:
Huff(a) = 0, Huff(b) = 10, Huff(c) = 1110, Huff(d) = 1111, Huff(r) = 110
e quindi, la codifica di w sull’alfabeto {0, 1} sarà:
Huff(w) = 0 10 110 0 1110 0 1111 0 10 110 0
a b
r a
c
a
d
a b
r a
di lunghezza 23.
Casi limite della codifica di Huffman sono collegati alla sequenza di Fibonacci. Infatti se le frequenze dei caratteri coincidono con i termini della
successione di Fibonacci, l’albero risultante appare bilanciato tutto da una
parte, quindi la lunghezza dei codici per ogni carattere, a partire da quello
più frequente che sarà codificato con un bit, aumenterà di un bit per ogni
carattere man mano che si scende nell’albero. Solo i due caratteri meno
frequenti avranno un codice della stessa lunghezza, differente soltanto per
l’ultimo bit.
Vediamo adesso la decodifica. L’algoritmo di Huffman è lossless, quindi
è caratterizzato da una funzione iniettiva. Il fatto che il codice creato è
prefisso fa sı̀ che la suddivisione di Huff(w) in codifiche di simboli, e dunque
la decodifica, sia unica.
Il principale difetto dell’algoritmo di Huffman è che il testo in input deve
essere letto due volte: la prima per calcolare le frequenze delle lettere, e
la seconda per codificare il testo. Si potrebbe risolvere il problema qualora
si considerassero delle frequenze medie; in questo modo, però, l’algoritmo
non assicurerebbe, ovviamente, la lunghezza minima del testo codificato.
Un’alternativa per risolvere il problema è data dall’algoritmo adattativo di
Huffman che costruisce l’albero e lo modifica man mano che legge il testo.
16
3.2
Codifica di Shannon-Fano
Il primo algoritmo famoso di codifica di simboli è stato introdotto alla fine
degli anni ’40 contemporaneamente da Shannon nei laboratori Bell e da Fano
al M.I.T. Analogamente a quanto visto per la codifica di Huffman, questo
è un algoritmo statistico che si basa sulla probabilità di ogni simbolo di
presentarsi all’interno del messaggio. Le codifiche ottenute saranno tali che:
• la codifica di ogni simbolo sarà differente da quella di ogni altro, dunque
la decodifica sarà unica;
• codifiche di simboli con bassa probabilità occuperanno più bits, viceversa codifiche di simboli con alta probabilità richiederanno un numero
minore di bits.
Algoritmo di Shannon-Fano (costruzione dell’albero di Shannon-Fano)
L’algoritmo di Shannon-Fano e quello di Huffman sono molto simili: differiscono solo nella costruzione dell’albero. Infatti, mentre l’albero di Huffman viene costruito a partire dalle foglie per poi risalire alla radice (“bottomup”), quello di Shannon-Fano viene, invece, costruito dall’alto verso il basso
(“top-down”). Nonostante siano simili, però, l’algoritmo di Huffman è preferibile perché porta a risultati migliori.
Descriviamo allora questo nuovo algoritmo:
• Data una lista di simboli, costruiamo una tabella delle probabilità per
ognuno di essi contando le loro occorrenze nel testo;
• ordiniamo in maniera decrescente secondo le probabilità i simboli di cui
sopra;
• creiamo un albero costituito dalla sola radice, associato alla tabella
intera;
17
• ripetiamo iterativamente, finché ad ogni simbolo non corrisponda una
foglia dell’albero associato alla tabella, le tre operazioni seguenti:
i) suddividiamo la tabella data in due sottotabelle in modo tale che la
somma delle occorrenze dei simboli della prima sia il più possibile
vicina a quella della seconda;
ii) concateniamo alle codifiche dei simboli della prima sottotabella
la codifica binaria 0, a quelli del secondo 1 e in corrispondenza
creiamo due figli del nodo associato alla tabella, il figlio sinistro
associato alla prima sottotabella, il figlio destro alla seconda;
iii) applichiamo la i) alle nuove tabelle.
Dal momento che abbiamo per ben due volte la possibilità di fare delle
scelte arbitrarie, nella suddivisione di ogni tabella e nell’assegnazione delle
etichette ai rami (0 al sinistro e 1 al destro o viceversa), la codifica di
Shannon-Fano non porta ad un unico risultato.
Esempio: Consideriamo lo stesso esempio di sopra, cioè
s = abracadabra.
Esaminando le occorrenze, e quindi le probabilità, delle singole lettere di
s, ed ordinandole decrescentemente, otteniamo
Simboli
Probabilita‘
a
b
r
c
d
5
2
2
1
1
Consideriamo adesso la i) e la ii): applicandole una prima volta otteniamo
18
Prima
Suddivisione
Simboli
Probabilita‘
a
5
0
b
r
c
2
2
1
1
1
d
1
1
1
ed iterativamente, tramite la iii), la tabella seguente.
Prima
Suddivisione
Terza
Suddivisione
Seconda
Suddivisione
Quarta
Suddivisione
Simboli
Probabilita‘
Codifiche
a
5
0
b
2
100
r
2
101
c
1
110
d
1
111
L’albero relativo alla codifica di Shannon-Fano appena effettuata di s =
abracadabra è
19
RADICE
0
1
a
0
0
b
1
1
0
r
c
1
d
Le parole di {0, 1}∗ associate alle lettere a, b, c, d, r sono:
SF (a) = 0, SF (b) = 100, SF (c) = 110, SF (d) = 111, SF (r) = 101.
La codifica di s sull’alfabeto {0, 1} è, dunque:
SF (s) = 0 100 101 0 110 0 111 0 100 101 0
a b r a c a d a b r a
di lunghezza 23.
In generale, Huffman porta a risultati di gran lunga migliori di quelli
ottenuti con l’applicazione di Shannon-Fano.
3.3
Codici aritmetici
Negli anni ’80 sono stati introdotti nuovi tipi di algoritmi statistici, i codici
aritmetici, che hanno ovviato ad alcuni problemi che si presentavano con
20
l’algoritmo di Huffman. Infatti, come vedremo, i codici aritmetici codificano
simboli, o gruppi di simboli, con numeri decimali, e quindi permettono di
adoperare per codifica numeri frazionari di bits. Il codice di Huffman, invece,
associa un intero ad ogni elemento della sorgente, il che porta ad un dispendio
eccessivo in termini di memoria. Se esaminiamo un solo simbolo, ovviamente,
i risultati ottenuti con i due diversi algoritmi saranno molto simili; ma una
volta che esaminiamo un testo lungo, la somma degli arrotondamenti (tali
si possono considerare i bits adoperati dalla codifica di Huffman rispetto a
quelli dei codici aritmetici) per i singoli simboli porta ad una differenza netta
con i risultati ottenuti con i codici aritmetici.
Descriviamo adesso questi nuovi algoritmi; essi si basano sul fatto che,
una volta note le probabilità dei singoli simboli di un alfabeto A di comparire
in una stringa data, si può suddividere l’intervallo [0, 1) in tanti suoi sottointervalli, in modo tale che ad ogni stringa di elementi dell’alfabeto sia associato
uno di essi. Grazie a questo algoritmo sia l’encoder che il decoder lavorano
on-line. Infatti, esaminando la stringa l’encoder può direttamente considerare carattere per carattere ed associare delle codifiche ad ogni gruppo di
simboli esaminati; il decoder a sua volta, riuscirà a risalire immediatamente
alla decodifica. Per chiarire meglio il concetto facciamo un esempio.
Esempio: Supponiamo di non considerare la stringa, già più volte esaminata, abracadabra, ma per semplicità una sua sottostringa
s = abracadabr,
in modo da potere suddividere più facilmente l’intervallo [0, 1) e da rendere
cosı̀ maggiormente comprensibile l’esempio stesso. Le probabilità delle singole lettere saranno:
na = 4, nb = 2, nc = 1, nd = 1, nr = 2.
21
Considerando solo alcune delle possibili concatenazioni di lettere, otteniamo la seguente tabella, nella quale è stato dato un particolare ordine ai
caratteri, ma bisogna sottolineare che questo può essere cambiato in qualsiasi
altra maniera.
Sottostringhe
a
b
c
d
r
aa
ab
ac
ad
ar
4
Probabilità
[0,.4)
[.4,.6)
[.6,.7)
[.7,.8)
[.8,1)
[0,.16)
[.16,.24)
[.24,.28)
[.28,.32)
[.32,.4)
I compressori linguistici
Gli algoritmi di Lempel e Ziv si inquadrano tra quegli algoritmi di compressione che analizzano le proprietà “strutturali” o “linguistiche” del testo (cioè
il fatto che certe concatenazioni di caratteri possano comparire, mentre altre
non sono presenti) per potere ridurre le dimensioni dello stesso.
Questi tipi di codifica che introdurremo ora si basano sulla possibilità di
effettuare sostituzioni all’interno della stringa. Il principio su cui ci si basano
è che possano esistere delle sottostringhe dell’input che si ripetono, e quindi
che si possa sostituire ognuna di esse con un puntatore (chiamato codeword)
alla posizione in cui questa stessa si è presentata per la prima volta all’interno
del testo. L’output dell’algoritmo descritto, quindi, sarà una successione di
caratteri dell’alfabeto sorgente, intervallati da alcune codewords. Dal momento che si potrebbe presentare anche la possibilità di avere come input
22
un singolo carattere, dobbiamo essere in grado di potere rappresentare anche
questo con un puntatore, quello al carattere stesso. Generalizzando, possiamo
assumere che l’output di una qualsiasi stringa sia una successione di codewords (si presenteranno due diversi tipi di puntatori: quelli a stringhe e quelli
ai caratteri stessi da cui sono richiamati). Un altro modo di rappresentare
l’output è quello di creare una lista di stringhe, o dizionario, rappresentante
i singoli fattori in cui viene suddiviso l’input dato.
Tra gli algoritmi che sfruttano le sostituzioni, l’algoritmo di Lempel e Ziv
è, senza dubbio, uno dei più importanti nel campo della compressione ed ha
riscosso successo soprattutto per le sue applicazioni. Più precisamente le sue
numerose varianti costituiscono probabilmente l’algoritmo in uso più diffuso
(tra di esse vi è, per esempio, la utility “compress” del sistema UNIX).
Esistono due algoritmi di Lempel e Ziv, uno risalente al 1977, LZ77, ed
uno al 1978, LZ78. A queste ne va affiancato un terzo, LZW, che rappresenta
l’implementazione da parte di Terry Welch di LZ78. Va, infine, tenuto conto
delle altre versioni introdotte da numerosi studiosi per migliorare sempre più
i risultati ottenuti.
4.1
LZ77: una compressione sliding window
Nel 1977 Lempel e Ziv pubblicarono un articolo, A Universal Algorithm for
Sequential Data Compression nel quale introducevano un nuovo algoritmo di
compressione dati, LZ77.
La struttura principale di questo algoritmo è una “finestra di testo” (chiamata sliding window per i motivi che adesso vedremo) di piccole dimensioni,
suddivisa in due parti. La prima di esse rappresenta il corpo principale ed
è costituita da un insieme, la cui cardinalità dipenderà dall’ampiezza della
sliding window, di elementi di s recentemente codificati. La seconda, invece,
di dimensioni notevolmente minori, è un look-ahead buffer, cioè una fine-
23
stra contenente alcuni caratteri non ancora esaminati di s, immediatamente
successivi a quelli del corpo principale, per la codifica dei quali è necessario
“guardare indietro” nella sliding window. In genere la prima contiene al suo
interno alcune migliaia di caratteri, il look-ahead buffer, invece, da 10 a 100.
Scopo dell’algoritmo è quello di codificare s facendo scorrere la sliding
window all’interno di esso. Più precisamente, noi esaminiamo il testo in
input poco per volta, considerando la finestra di testo che man mano si sposta
lungo lo stesso, e cerchiamo l’esistenza nel corpo principale, che rappresenta
il dizionario, di una stringa che combaci con almeno una parte di quella
contenuta nel look-ahead buffer. In tal modo otteniamo una codifica data
dalla tripla:
a) posizione all’interno del corpo principale del primo carattere della più
lunga sottostringa comune (essa potrà avere anche lunghezza 0);
b) lunghezza della sottostringa di cui al punto a);
c) carattere ad essa successivo nel look-ahead buffer.
Esempio:
Supponiamo di considerare
s = abracadabra abracadabra abracadabra,
e che ad un certo istante t la finestra sia quella descritta dalla figura seguente.
abracadabra abracadabra abra
corpo principale
Look-Ahead Buffer
24
Notiamo che la stringa ’ abra’ è interamente contenuta nel dizionario e la
codifichiamo tramite la tripla (12,5,”). Infatti la posizione nel corpo principale del carattere iniziale della prima occorrenza della stringa data è 12, la
sua lunghezza è 5 ed infine non abbiamo caratteri aggiuntivi, in quanto il
look-ahead buffer contiene solo questa sottostringa di s.
Dopo avere effettuato questa codifica la finestra si sposta esattamente di
tanti posti quanto è la lunghezza della stringa codificata (nel nostro caso
5) e viene esaminata una nuova stringa rispetto ad un nuovo dizionario.
Otteniamo, dunque,
adabra abracadabra abra
corpo principale
4.2
cadab
Look-Ahead Buffer
Problemi derivanti dall’uso di LZ77
L’algoritmo LZ77, però, andava incontro a vari problemi derivanti dalla limitatezza della sliding window. Più esattamente, l’avere imposto che il corpo
principale, cioè il dizionario, fosse limitato faceva sı̀ che una parola ripetuta
spesso all’interno di un testo molto lungo, come può essere nel nostro caso il
termine “compressione”, poteva essere richiamata raramente proprio perché
raro era il caso in cui si potevano trovare due occorrenze della stessa vicine
tra di loro. Un altro problema era correlato all’ampiezza limitata del lookahead buffer; per questo motivo non si potevano avere puntatori a parole
lunghe, anche quando se ne fosse presentata l’occasione.
Esempio
25
Supponiamo di riconsiderare l’esempio del paragrafo precedente
abracadabra abracadabra abracadabra
e di aggiungere dopo il look-ahead buffer qualche altro carattere successivo
di s.
abracadabra abracadabra
corpo principale
abra
cadabra
Look-Ahead Buffer
In questo caso, anche se fosse possibile richiamare l’intera parola abracadabra,
dovremmo considerare solo la sua sottostringa abra, il che limita di gran lunga
i risultati ottenuti e porta a coefficienti non del tutto esaurienti. (Ovviamente
in caso di testi all’interno dei quali abbiamo poche ripetizioni LZ77 conserva
ancora tutta la sua efficienza).
Si potrebbe pensare di risolvere il problema aumentando le dimensioni
della finestra, sia del dizionario che del buffer, ma anche questo porta delle
difficoltà. Se noi aumentiamo l’ampiezza del dizionario, per esempio, da
4K a 64K, abbiamo bisogno di 4 bits suppletivi per codificare la posizione
della stringa richiamata; esattamente invece di 12 bits dovremo utilizzarne 16
(ricordiamo che 212 = 4096 e 216 = 65536). Inoltre, l’aumento di dimensione
del buffer da 16 bits a 1K comporta l’uso non più di 4 ma di 10 bits per
codificare la lunghezza di una frase (24 = 16, 210 = 1024). Tutto ciò porta,
quindi, ad un incremento del costo necessario per codificare una stringa da 17
a 27 bits, il che provoca un notevole aumento del coefficiente di compressione,
e quindi una corrispondente diminuzione dell’efficienza dell’algoritmo dato.
26
4.3
LZ78: un nuovo algoritmo
Di tutti i problemi derivanti da LZ77 si resero conto gli stessi Lempel e Ziv
che nel 1978 pubblicarono un articolo, Compression of Individual Sequences
via Variable-Rate Coding, nel quale illustravano un nuovo algoritmo, LZ78,
molto simile a LZ77 ma differente da esso nella descrizione del dizionario
(questa versione rappresenta una compressione universale ottimale su sorgenti fattoriali).
LZ78 abbandona il concetto della finestra di testo: se LZ77 teneva conto di
un dizionario di stringhe definite all’interno di una finestra fissata e finita, con
LZ78 il dizionario diventa un insieme potenzialmente illimitato di stringhe.
Questo nuovo algoritmo somiglia a quello precedente in molti suoi aspetti:
per esempio LZ77 dava in output un insieme di triple (la posizione della
precedente occorrenza della stringa, la lunghezza della stessa e il carattere
ad essa seguente); un medesimo output viene dato da LZ78, facendo eccezione
per la lunghezza dell’espressione che non è necessaria dato che il decoder già
la conosce.
Le uniche differenze tra i due algoritmi si riscontrano proprio in quei
punti essenziali a far sı̀ che LZ78 sia molto più efficiente di LZ77, cioè che
dia risultati migliori. Infatti, invece che una sliding window di dimensione
prefissata, LZ78 utilizza un dizionario la cui dimensione cresce man mano che
viene esaminato il testo. Le stringhe del dizionario saranno richiamate ogni
qualvolta sarà necessario ed inoltre in qualsiasi momento, anche dopo avere
esaminato milioni di ulteriori caratteri (contrariamente a quanto avveniva
per LZ77 con il quale una stringa veniva richiamata solo se ad una piccola
distanza dal look-ahead buffer).
Esaminiamo adesso più da vicino questo nuovo algoritmo. La funzione
totale LZ : A∗ → 2∗ lavora nel modo seguente: considerata una qualsiasi
parola w ∈ A∗ , per essa troviamo una fattorizzazione unica definita da:
27
n ∈ IN + ,
w = w0 w1 · · · wn
in modo che:
• w0 sia la parola vuota;
• per ogni i tale che 1 ≤ i ≤ (n − 1), wi è il più lungo prefisso di wi · · · wn
che sia possibile scrivere nella forma wi = wji ai , con ai ∈ A e ji < i;
• wn = wjn , con jn < n.
Dunque il primo fattore deve essere vuoto ed ogni altro, tranne l’ultimo,
deve essere costituito da un fattore precedentemente incontrato seguito da
un elemento di A. È ovvio che bisogna scegliere una giusta struttura dati per
rappresentare tale dizionario in maniera tale che l’algoritmo risulti efficiente.
Tra le possibili rappresentazioni in memoria del dizionario, si può utilizzare
un albero A(w) in cui vengono immesse le parole wi . In tale albero i rami
sono etichettati da elementi di A tali che figli dello stesso padre siano collegati
ad esso tramite rami aventi labels diverse. In particolare per la codifica del
dizionario di LZ78 possiamo utilizzare un patricia tree, avente al più 256
(quanti sono i caratteri ASCII) figli per ogni nodo. Codificare il testo nel
suo corrispondente binario prima di comprimerlo può essere utile non solo
per riuscire ad ottenere una quantità maggiore di ripetizioni, ma anche per
potere semplificare la struttura dati utilizzata per rappresentare l’albero, che
cosı̀ diventa binario.
Ogni fattore wi corrisponde ad un nodo di A(w) e, labellandolo con i, si
può facilmente vedere che la condizione di iniettività richiesta ad ogni lossless
data compression viene verificata (basta considerare l’applicazione
w → (A(w), jn )).
28
Per effettuare l’operazione di decodifica, bisogna ricostruire A(w) cosı̀ come
lo si costruisce in fase di codifica e da questo si ottengono i fattori wi di
w. Dunque l’output deve essere tale da potere effettuare una ricostruzione
sincronizzata dell’albero dato.
Descriviamo adesso l’output del nostro algoritmo.
Ogni fattore wi , 1 ≤ i ≤ (n − 1), viene trasmesso tramite la coppia
(ji , ai ), mentre wn tramite jn . Dal momento che per trasmettere ji abbiamo
bisogno di dlog(i)e bits (necessari e sufficienti per specificare uno qualsiasi
tra 0, 1, ..., i − 1), e che il carattere ai può trasmettere se stesso, allora la
lunghezza dell’output dipenderà esclusivamente dal numero (n − 1) di rami
di A(w). Otterremo quindi, per un’opportuna costante K:
| LZ(w) |=
n
X
dlog(i)e + K(n − 1).
i=1
Tenuto conto che dlog(i)e ≤ 1 + log(n − 1)1 , otteniamo:
| LZ(w) |≤ n[1 + log(n − 1)] + K(n − 1) ≤ (n − 1) log(n − 1) + K 0 (n − 1).
con K 0 costante opportuna dipendente da A, costante che può essere anche
negativa. Dunque, comunque sia fatto questo albero A(w), l’output dipende
solamente da n − 1 numeri di lunghezza predeterminata (al più dlog(n − 1)e)
e da n − 1 caratteri di A. Tenuto conto, però, che il termine dominante nella
somma è il primo, notiamo che K 0 non è influente nel calcolo del coefficiente
di compressione.
1
La diseguaglianza dlog(i)e ≤ 1 + log(n − 1) vale perché:
• per ogni i ≤ (n − 1) risulta dlog(i)e ≤ 1 + log(i) ≤ 1 + log(n − 1),
• dlog(n)e ≤ 1 + log(n − 1)
29
Analizziamo adesso la lunghezza dell’input w in funzione dell’albero costruito a partire da esso. Ogni fattore wi influisce su | w | esattamente in
misura pari alla profondità del vertice i, denotata con height(i), nell’albero
dato. Otterremo, pertanto:
| w |= height(jn ) +
n−1
X
height(i).
i=1
P
Il termine dominante della somma soprascritta, n−1
i=1 height(i), dipende
esclusivamente dalla forma dell’albero e viene denominato internal path length
dell’albero dato.
LZ78, inoltre, rappresenta una compressione continua.
Per definire rigorosamente la continuità conviene collocarsi nell’ambito
delle parole infinite. Denotiamo con Aω l’insieme delle parole infinite su A.
La metrica rispetto a cui la compressione risulta continua è quella del “più
lungo prefisso comune”. Definiamo questa metrica d nel seguente modo: date
due parole x e y appartenenti ad Aω diremo che:
• d(x, y) = 0, se le due parole sono uguali;
• d(x, y) = 21a , se x coincide con y solo nei primi a caratteri, ovvero se
esistono x0 prefisso di x e y 0 prefisso di y, tali che | x0 |=| y 0 |= a, con
x0 e y 0 i più lunghi prefissi rispettivamente di x e di y soddisfacenti tale
proprietà.
30
x’
x
y’
y
Esempi:
1. Se x e y sono due parole infinite uguali, allora d(x, y) = 0;
2. se x e y, invece, coincidono per intero tranne che nel primo carattere,
allora a = 0 e quindi d(x, y) = 1.
Proviamo adesso che la funzione LZ è continua rispetto alla distanza
appena definita. Ciò equivale a dimostrare che:
lim LZ(x) = LZ(y)
x→y
Ma che significa che x → y? Significa che d(x, y) → 0, cioè che, se x0 è il
più lungo prefisso comune a x e y, 2|x1 0 | → 0, quindi che | x0 |→ ∞, cioè ancora
che x e y coincidono tranne che in al più un numero finito di caratteri finali,
quindi gli alberi LZ(x) e LZ(y) coincidono tranne che in al più un numero
finito di rami, da cui LZ(x) → LZ(y). Dunque, otteniamo la seguente:
Proposizione 4.1 LZ : A∗ → 2∗ è una compressione continua.
31
Sia w ∈ A∗ tale che A(w) abbia a rami, sia I l’internal path length di A(w)
e sia τ il coefficiente di compressione2 di LZ, allora:
τ (w) ≤
alog(a) + Ka
,
I
con K costante dipendente da A.
Riassumiamo adesso il procedimento adottato da LZ78 per potere fare lo
stesso esempio fatto per LZ77 e fare, quindi, i debiti paragoni. Il dizionario
viene inizializzato con la stringa vuota ²; man mano che si va avanti nel
testo viene aggiornato con nuove stringhe, date dalla concatenazione di una
“frase” precedente (la più lunga stringa comune al testo ed al dizionario, essa
potrebbe essere anche la prima stringa, quella vuota) con un nuovo carattere.
Il processo di codifica, ovviamente, termina non appena il cursore che si
muove all’interno del testo arriva alla fine dello stesso. Questo è ciò che dà
in output anche LZ77: la posizione all’interno della finestra della precedente
occorrenza dell’espressione data e il carattere aggiuntivo. LZ78 fa un ulteriore
passo, aggiunge questa nuova stringa al dizionario. Talvolta, però, LZ77 può
risultare più efficiente; è il caso in cui abbiamo un testo molto corto con
ripetizioni di frammenti dello stesso molto vicine tra di loro. È il caso, però,
anche di un testo lungo all’interno del quale non si abbiano ridondanze, o
comunque se ne presentino poche. In quest’ultima situazione LZ78 adopera
un dizionario di notevoli dimensioni senza che esso sia utilizzabile, ma solo
sciupando una notevole quantità di memoria; LZ77, al contrario, fa uso,
come dizionario, di una piccola finestra che scorre all’interno del testo e per
la quale, quindi, non si fa un uso spropositato di memoria. Si riscontra,
pertanto, una notevole differenza tra i risultati ottenuti, dal momento che
il dizionario di LZ78 non viene utilizzato quasi mai, ma apporta solo un
2
coefficiente definito come τ (w) =
|LZ(w)|
|w|
32
dispendio in termini di memoria e di tempo di calcolo (infatti dobbiamo
ricordare che la parte di testo da codificare deve essere confrontata con ogni
singola stringa del dizionario).
ESEMPIO: Facciamo lo stesso esempio di sopra:
abracadabra abracadabra abracadabra
Nel caso di compressione mediante l’utilizzo di LZ78 otteniamo la tabella
seguente, rappresentante per ogni stringa del dizionario il modo in cui la si
è ottenuta.
POSIZIONE NEL DIZIONARIO
DELLA STRINGA RICHIAMATA
CARATTERE
SUPPLETIVO
0
0
0
1
1
1
3
0
6
4
0
9
8
2
10
12
a
b
r
c
d
b
a
’ ’
r
a
d
a
a
r
d
ε
33
DIZIONARIO
POS.
STR.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ε
’a’
’b’
’r’
’ac’
’ad’
’ab’
’ra’
’ ’
’abr’
’aca’
’d’
’abra’
’ a’
’br’
’acad’
Per quanto riguarda, invece, l’albero della figura seguente, ho voluto
mostrare qualche fase della costruzione del dizionario, evidenziando quella
di inizializzazione (I) ed alcune di aggiornamento (II dopo un passo, III dopo
due, IV dopo 6).
a
b
a
a
c
I
II
III
d
b
r
b
IV
Alla fine dell’algoritmo l’albero rappresentante il dizionario sarà
34
a
c
4.4
d
b
a
r
d
a
b
a
r
d
’’
r
a
LZW
Nel 1984 Terry Welch pubblicò un articolo, A Technique for High-Performance
Data Compression, nel quale illustrava un nuovo algoritmo, LZW, basato su
LZ78.
Questo algoritmo si basa sulla costruzione di una tabella, dizionario, che
contiene stringhe e trasforma sequenze di caratteri dell’input dato in codici di lunghezza fissata. Questa tabella, che viene costruita man mano che
il testo viene esaminato, ha una proprietà molto importante: il prefisso di
ogni stringa in essa contenuta fa parte ancora di essa. Ciò significa che se nel
dizionario troviamo wa, con w stringa ed a carattere aggiuntivo, allora vi sarà
anche w. Per fare ciò il dizionario deve essere inizializzato con tutti i simboli dell’alfabeto. Ovviamente grazie a questo algoritmo si risparmia molto
35
tempo, però si presenta il problema per cui alcuni simboli poco diffusi occupano memoria senza essere necessari e il patricia tree assume, cosı̀, dimensioni notevoli senza motivo. Se consideriamo tutti i caratteri ASCII, infatti,
il dizionario contiene, già prima di iniziare la compressione, ben 256 stringhe
e la prima posizione possibile all’interno dello stesso sarà la 257-esima. Si
potrebbe ovviare a questo nuovo problema eliminando dal dizionario originale
esattamente quei simboli che non appariranno all’interno del testo in input.
Ricordiamo, inoltre, che se un dizionario di 256 stringhe comporta l’uso di
8 bits, uno che ne contenga un numero compreso tra 257 e 512 impiegherà
9 bits e se facciamo un esame in termini di bytes, basta avere anche una
sola stringa in più, cioè 257, per avere bisogno non più di un byte, ma di
due, spreco eccessivo soprattutto per un algoritmo di compressione. Questo
è forse l’unico difetto di LZW.
Esempio: Consideriamo sempre lo stesso esempio:
abracadabra abracadabra abracadabra.
Le nuove stringhe possono essere racchiuse nella tabella seguente.
36
NUOVE STRINGHE DEL DIZIONARIO
256 = ’ab’
257 = ’br’
258 = ’ra’
259 = ’ac’
260 = ’ca’
261 = ’ad’
262 = ’da’
263 =’abr’
264 = ’ra’
265 = ’ a’
266 =’abra’
267 = ’aca’
268 = ’ada’
269 =’abra’
Ricordo, però, che questa non coincide con il dizionario; infatti, per ottenere il
risultato finale dobbiamo aggiungere al risultato ottenuto le stringhe iniziali,
cioè quelle coincidenti con i singoli caratteri. Saranno perciò necessari 9 bits.
La scoperta di Welch sta nell’avere limitato la quantità di bits da usare per
codificare un qualsiasi testo. Lempel e Ziv, infatti, da “buoni matematici”
avevano ipotizzato di potere usare un numero infinito di bits, cosa impossibile
dato che il computer è una macchina fisica e quindi finita. Welch, invece,
prova che sono sufficienti 13 bits. Infatti, non appena il dizionario contiene
8191 (213 = 8192) stringhe procediamo nel seguente modo: eliminiamo le
codifiche non adoperate e shiftiamo quelle rimaste in modo da lasciare spazio
libero alla fine della tabella; se cosı̀ non può essere, cioè tutte le codifiche
sono state utilizzate, consideriamo quelle richiamate più recentemente e più
37
frequentemente ed eliminiamo le altre. In questo modo otterremo il risultato
di potere utilizzare una quantità finita di bits, esattamente al più 13, per
codificare un testo di dimensioni qualsiasi, paradossalmente anche infinite.
38