UNIVERSITA’ DEGLI STUDI DI CAGLIARI
DIPARTIMENTO DI INGEGNERIA MECCANICA
RELAZIONE COMPORTAMENTO
MECCANICO DEI MATERIALI:
METODI OTTICI
Relazione a cura di:
Mattia Lai 45295
Andrea Aresu 45198
Roberto Martis 43234
Domenico Bradascio 43108
Carlo Dubois 45316
Pietro Luigi Pala 45175
Giovanni Tuscano 45232
1
2
Sommario
1
Introduzione ................................................................................................................................. 4
2
Metodo a variazione di fase ......................................................................................................... 4
2.1
Phase shifting ........................................................................................................................ 5
3
Applicazione del metodo a variazione di fase .............................................................................. 6
4
Listato Matlab ............................................................................................................................... 9
5
Conclusioni.................................................................................................................................. 10
3
1
Introduzione
Gli attuali strumenti per il rilievo di forma consentono di riprodurre con un’elevata accuratezza e
ripetibilità le caratteristiche geometriche di oggetti anche complessi. Per questo motivo il loro
impiego è in continua crescita: dal Reverse Engineering (RE) per l'analisi della concorrenza al
controllo di qualità di prodotti industriali; dalla creazione di modelli da inserire in ambienti creati
attraverso la realtà virtuale alla ricostruzione o al restauro di manufatti appartenenti al campo dei
beni culturali. In questa esercitazione è stata usata la tecnica interferometrica a scorrimento di
fase (phase-shift), utilizzata comunemente per il rilievo di forme in 3D. Nella meccanica
sperimentale viene utilizzato per rilevare deformazioni.
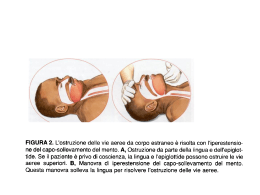
Nel lavoro viene proposta la rilevazione di un oggetto, nella fattispecie la testa di un manichino.
L’esperienza potrebbe essere anche intesa come rilevazione di una deformazione avente la forma
dell’oggetto in esame.
2
Metodo a variazione di fase
La tecnica interferometrica a scorrimento di fase (phase-shift) rientra nella categoria dei sistemi
intrinsecamente 3D basati sull’utilizzo della tecnica PMP (phase measurement profilometry) più
comunemente nota con la denominazione di metodo ‘phase shifting’. La configurazione di prova
prevede l’utilizzo di una fotocamera reflex e di un proiettore per la proiezione delle frange. Nel
seguito si ritiene utile descrivere brevemente i principi teorici che caratterizzano il funzionamento
del metodo utilizzato.
Figura 2.1 Configurazione di prova
4
2.1 Phase shifting
Attraverso la tecnica PMP (phase measurement profilometry), più comunemente nota con la
denominazione di metodo ‘phase shift’, viene creata un’immagine con frange parallele, profilo
sinusoidale e passo fisso; questa immagine viene poi proiettata variando l’angolo di fase delle
frange in modo che queste appaiano scorrere sulla superficie del pezzo. Contemporaneamente
alle proiezioni, la macchina fotografica acquisisce una sequenza di immagini in cui il tono di grigio
di ciascun pixel varia sinusoidalmente con una frequenza pari a quella delle frange proiettate ed
un angolo di fase dipendente dalla posizione nello spazio dell’areola della superficie inquadrata.
Utilizzando, ad esempio quattro acquisizioni sfasate di 90° l’una rispetto all’altra:
per α1=0
per α2=90°
(
per α3=180°
(
)
)
(
)
per α4=270°
Combinando le relazioni precedenti si ottiene la fase ϕf che è denominata fase frazionaria:
Si passa quindi dalla fase frazionaria alla fase totale utilizzando la procedura di identificazione
(unwrapping), basata sull’eliminazione dei salti che subisce la fase frazionaria.
5
3
Applicazione del metodo a variazione di fase
In questa esercitazione sono state acquisite otto immagini, quattro del solo fondo e quattro
inserendo l’oggetto in scena; ognuna delle quattro immagini, in entrambi i casi, è scattata
proiettando un campo di luce con intensità che varia sinusoidalmente, con uno sfasamento che
cresce a step di 90° come precedentemente descritto.
Figura 3.1 Immagini sfasate convertite in scala di grigi
Gray value
Le immagini sono state acquisite come matrici su Matlab per essere elaborate. Ogni pixel viene
convertito in un elemento di matrice che ha un valore dipendente dal colore che possiede e
proporzionale all’intensità di luce.
Effettuando il plot di una riga di ogni matrice delle 4 immagini del fondo si può vedere come
l’intensità di luce abbia effettivamente un andamento sinusoidale.
Figura 3.2 Andamento segnale per pixel
Distance (pixel)
6
Gray value
Elaborando le 4 immagini è stata ottenuta, secondo la formula riportata in precedenza, un’unica
matrice contenente la fase variabile tra 0° e 360°di ogni pixel. Sono state ottenute quindi due
matrici, una per il solo fondo ed una per il fondo più l’oggetto.
Effettuando un plot di una riga della matrice del fondo si può notare l’andamento a dente di sega.
Distance (pixel)
Figura 3.3 Andamento segnale fase frazionaria
Prima di passare alla visualizzazione dell’immagine in 3D tramite Matlab è necessario eseguire un
unwrapping sulle matici. In questarelazione non si entra nel merito delle equazioni
dell’unwrapping in quanto questo è stato eseguito con il pront dei comandi di Linux insieme al
professor Baldi. L’effetto di questo metodo è proposto nelle figure 3.3 e 3.4:
Figura 3.3 Proiezione frange e plot segnale wrapped
Figura 3.4 Proiezione frange e plot segnale unwrapped
7
La forma della superficie è estratta dall’osservazione del modello delle frange, dove l’incremento
dell’altezza è espresso dalla formula:
Dove Pp-Pa è la differenza della proiezione delle frange su una superficie piana e il periodo
apparente delle frange proiettate nell’oggetto.
Figura 3.5 immagine 3D visualizzata con Matlab
8
4
Listato Matlab
clc
clear all
%DETERMINAZIONE FASE FRAZIONARIA
%foto fondo%
I1=imread('CRW_5866.tif');
I2=imread('CRW_5867.tif');
I3=imread('CRW_5868.tif');
I4=imread('CRW_5869.tif');
fi= atan2(double(I4)-double(I2),double(I1)-double(I3));
fic = fi(230:675,511:882);
%foto con testa;
I1p=imread('CRW_5874.tif');
I2p=imread('CRW_5875.tif');
I3p=imread('CRW_5876.tif');
I4p=imread('CRW_5877.tif');
fip= atan2(double(I4p)-double(I2p),double(I1p)-double(I3p));
fipc = fip(230:675,511:882);
%maschera;
Maschera=imread('maschera.tif');
maschera = double(Maschera(230:675,511:882));
%stampa dati per unwraping
dlmwrite('fi_senza_niente.txt', fic);
dlmwrite('fip_con_testa.txt', fipc);
dlmwrite('maschera.txt', maschera);
%acquisizione immagini dopo unwrapping
Pp=load('fondo.dat');
Pa=load('oggetto.dat');
alfa=tand(26.43);
deltah=(Pp-Pa)/alfa;
figure(1);
imagesc(deltah(1:446,1:372));
dlmwrite('Finale.txt', deltah);
9
5
Conclusioni
Questa esperienza ha permesso di conoscere un valido metodo per la valutazione delle
deformazioni, con una semplice configurazione di misura.
Durante l’esercitazione sono state riscontrate delle difficoltà che non hanno permesso una
perfetta ricostruzione 3D della testa.
In particolare la prima difficoltà è stata quella di eliminare la non planarità della proiezione delle
frange.
Successivamente sono stati riscontrati dei problemi che avrebbero causato del rumore, come ad
esempio il materiale della testa, che essendo in velluto disturbava la proiezione delle frange a
livello del contorno della sagoma. E’ stato poi opportuno effettuare una maschera per eliminare il
rumore dovuto all’ombra e parzialmente a quello del materiale, come illustrato nella figura 5.1.
Figura 5.1 Maschera
In ultima analisi durante l’acquisizione ed elaborazione con i software sono state perse
informazioni sui pixel perché si è passati da immagini a 12 bit ad immagini ad 8 bit.
In conclusione con buona approssimazione è stato ottenuto un modello in 3-D di un piano in cui è
stato impresso una testa di manichino.
10