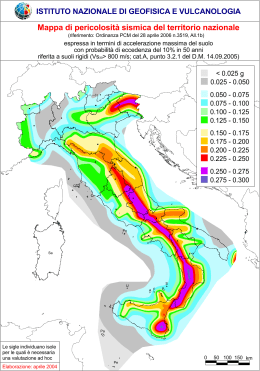
CORSO DI MICROZONAZIONE SISMICA E VALUTAZIONE DELLA
RISPOSTA SISMICA LOCALE PER LA RICOSTRUZIONE POSTPOST
TERREMOTO
La pericolosità sismica
Dario Albarello
Dipartimento di Scienze Fisiche
Fisiche, della Terra e dell’Ambiente
dell Ambiente
Università degli Studi di Siena
[email protected]
Auditorium Reiss Romoli – Coppito (AQ), 20 Febbraio 2013
Scopo di questa breve esposizione è illustrare
quello
ll che
h c’è
’è di
dietro
t lle carte
t di pericolosità:
i l ità
come vengono costruite, quali le assunzioni di
base e i limiti
La presentazione viene articolata in tre parti
1. La previsione in forma probabilistica: Il “quando”,
il “dove” e il "come” del terremoto atteso
2. L’approccio Statistico con elementi deterministici
3 Possibili risultati
3.
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
La previsione
Obiettivo (ideale) della stima della pericolosità sismica è quello di
valutare le caratteristiche dello scuotimento sismico atteso in un dato
punto
t del
d l tterritorio:
it i sii ttratta
tt di ffatto
tt un tentativo
t t ti di “previsione”
“
i i
” del
d l
terremoto
La via maestra per raggiungere questo obiettivo sarebbe quella di
utilizzare un modello fisico capace
p
di rappresentare
pp
con sufficiente
dettaglio il fenomeno atteso e quindi permettere di valutarne l’evoluzione
(tipo “previsione delle eclissi solari”)
In verità si sanno molte cose sui terremoti:
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
1. Sappiamo che i terremoti sono dovuti a
scorrimenti rapidi lungo superfici di frattura
(faglie) all’interno
all interno della crosta
2. Che queste fratture sono provocate da
fenomeni a grande scala (deriva dei
continenti) caratterizzati in Italia da tassi di
deformazione piuttosto bassi (dell’ordine di
10-7 y-1)
3 Sappiamo che lo scuotimento del suolo è
3.
provocato dalla propagazione di energia in
forma di onde sismiche dalla sorgente ala
superficie del suolo e che questa
propagazione avviene con modalità
descrivibili in dettaglio e con precisione
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
4. E’ anche possibile stabilire una relazione fra le caratteristiche della sorgente
(dimensione, ecc.) e la forma dello spettro di scuotimento atteso
E direttamente
E’
proporzionale alla
dimensione della
sorgente e
inversamente
proporzionale alla
distanza dalla
A(g)
(g)
sorgente
T (sec)
Effetto dell’assorbimento
dell’energia fra la sorgente e
il sito
La Pericolosità Sismica – D.Albarello
E’ proporzionale
alla lunghezza della
faglia
E’ proporzionale
alla entità della
dislocazione sulla
faglia
20 Febbraio 2013 – h.16.00‐17.00
A partire dallo spettro di ampiezza (e da quello di fase) dello scuotimento del
suolo è poi possibile risalire allo “spettro di risposta” utile nella progettazione
A(g)
Spettro di
risposta
(semplificato)
T (sec)
( )
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Quindi per effettuare la “previsione” bisognerebbe sapere:
1. dove la crosta terrestre si “romperà”
romperà dando origine al terremoto
(fino ad un attimo prima la crosta è da aspettarsi “integra”) a
partire dalle conoscenze sullo stato di deformazione in cui si
trova il volume di terreno che ospiterà il terremoto
2. dalle conoscenza della soglia di rottura e del tasso di
caricamento tettonico p
prevedere il momento della frattura
(quando avverrà)
3. Come avverrà la frattura (in quale direzione si propagherà, quali
eterogeneità incontrerà, ecc.)
4. come si propagheranno le onde sismiche dalla sorgente del
terremoto (l
(l’ipocentro)
ipocentro) fino al punto della superficie che ci
interessa
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
In realtà le difficoltà sono moltissime
1. Il punto di nucleazione dei terremoti si trova solitamente a profondità
dell’ordine di 10-20 Km dalla superficie, ovvero in una zona del tutto
inaccessibile all’esplorazione diretta
2. I tempi che caratterizzano la deformazione (“la carica” della molla)
sono assai lenti: per le faglie sismogeniche italiane si valutano tempi
che vanno fra alcune centinaia ad alcune migliaia
g
di anni necessari
a caricare una struttura fino a produrre un terremoto
3. La frattura ha una dinamica complessa, ancora poco nota anche in
l b t i iinoltre
laboratorio;
lt lla soglia
li e lla modalità
d lità di rottura
tt
di
dipende
d d
da una
molteplicità di fattori (presenza di fluidi, storia di carico, ecc.) che
sono in generale poco o per nulla noti
4. La forma dello scuotimento dipende dalle caratteristiche del
sottosuolo lungo il percorso delle onde (di decine o anche centinaia
di Km)
K ) e dalle
d ll modalità
d lità con cuii lla ffrattura
tt
avviene
i
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Partendo dall’ultimo punto: a che livello di dettaglio è necessario
conoscere le caratteristiche del mezzo per prevedere lo
scuotimento (ammesso di conoscere le caratteristiche della
frattura)?
IImmaginiamo
i i
che
h il periodo
i d d
dello
ll scuotimento
ti
t di iinteresse
t
sia
i di
0.5 sec (2 Hz) e che le fasi S siano le più interessanti ai fini della
valutazione del danno atteso
Assumendo velocità delle onde S nella crosta dell’ordine di 1000
m/sec, le lunghezze d’onda di interesse (λ=Vν) sono dell’ordine di
500 m: è questa la scala cui dovremmo conoscere le eterogeneità
presenti nella crosta. Più in superficie, a velocità più basse (400600 m/sec) la lunghezza d’onda diminuisce ancora (200-300 m)
Di fatto queste conoscenze di dettaglio non sono disponibili a
scala regionale
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Mondo “ideale”
Osservazioni
Q
Questo
t spiega
i
fenomeni
f
i di questo
t tipo
ti
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
La previsione in termini probabilistici
In queste condizioni, ogni “ipotesi” riguardo ai possibili scenari sismici futuri
diventa possibile
Questo non vuol dire però che tutti questi scenari siano ugualmente verosimili
rispetto alle conoscenze di cui disponiamo: alcuni scenari sono più verosimili
di altri
La maggiore o minore verosimiglianza viene espressa in forma di un valore di
probabilità
Tutte le conoscenze di cui disponiamo sono utilizzate per definire i diversi
valori di probabilità da associare a ciascuno scenario possibile
Scegliere come riferimento uno scenario invece che un altro sulla base di
queste probabilità è frutto di una scelta “politica” (più o meno consapevole)
E’come fare una scommessa: non ci sono certezze (non possiamo essere
certi di avere fatto la scelta giusta) ma solo rischi “calcolati” più o meno bene
Si può sbagliare per eccesso di cautela (e spendere troppo per la prevenzione)
o per eccesso di sicurezza (e spendere troppo poco)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
L’approccio statistico
Il problema è quindi quello di assegnare queste probabilità
In molti casi si ricorre ad un approccio empirico che valuta queste
probabilità su base statistica a partire da osservazioni su terremoti
passati
Prendiamo l’esempio della propagazione (a grande scala) dalla sorgente al
sito
In assenza di informazioni sufficientemente dettagliate, il problema viene
affrontato in modo empirico
1. Si assume un modello empirico semplificato che serva a “rappresentare
la propagazione”: in pratica si stabilisce una relazione empirica fra alcuni
elementi informativi semplici (energia liberata alla sorgente tramite la
magnitudo M, distanza r fra l’epicentro e il sito) in funzione di alcuni
parametri empirici (a, b, c e d nell’esempio che segue)
log Y = a + bm + c log(d 2 + h 2 )1 2
2. Sulla base di valori osservati vengono scelti i valori dei parametri che
meglio riproducono l’insieme delle osservazioni
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Si prendono le registrazioni ottenute
ad una rete accelerometrica
Si selezionano le sole stazioni su basamento sismico affiorante
(ovvero con Vs almeno pari a 800 m/sec)
Si selezionano tutte le registrazioni disponibili a queste stazioni per terremoti
collocati a varie distanze e caratterizzati da valori di magnitudo differente
Per ciascuna registrazione vengono individuati i parametri di interesse
(PGA, PGV, ordinate spettrali dello spettro di risposta)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
log10 Y = a + bm − log10 (r 2 + h 2 )1 2
Naturalmente si tratta di stime affette da
incertezza. Questa viene caratterizzata dal
parametro σ
(da Sabetta e Pugliese, 1996)
In pratica, sono possibili diversi valori di
accelerazione per la stessa distanza
epicentrale e la stessa magnitudo. Questi
gaussiana la
valori sono distribuiti come una g
cui ampiezza è determinata da σ
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
In questo modo è per esempio possibile stimare direttamente lo spettro di risposta del
terremoto atteso a p
partire dai valori di magnitudo
g
e distanza
Si tratta della stima del solo spettro di ampiezza: non c’è nessuna indicazione sulla fase
(questa dipenderebbe dai dettagli per percorso e non può essere ricavata in questo modo)
Att
Attenzione:
i
sii ttratta
tt di una stima
ti
assaii iincerta!
t !
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Conviene fare qualche conto per capire quanto sia grande l’incertezza
associata a questa stima dello scuotimento (“quanto è larga la campana”)
Se σ ha un valore di pari a 0.2 del log10 A, il 68% dei valori possibili sarà
compreso nell’intervallo compreso fra + e – 0.2 dalla media ((del log
g10 A):
) cosa
vuol dire in termini di Accelerazione?
[
log10 A ± 0.2 → 10 A,10
0.2
− 0.2
]
∆A
∆A
A→
= 100.2 − 10 −0.2 = 0.9 = 90%
A
Sono ragionevolmente possibili valori di accelerazione che, a parità di
distanza e magnitudo, possono scostarsi dal valore atteso fino al 90%
aspettare incertezze sul valore stimato dell’ordine del 100% !
Faccio notare che in queste condizioni, fornire un valore di
accelerazione con tre decimali o più è totalmente privo di senso ed ha
solo un valore formale
Si noti anche che il valore ottenuto è quello medio che , nell’ipotesi di
distribuzione log
log-normale,
normale ha una probabilità di essere superato pari al 50%
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Cosa dire del “dove” saranno localizzate le future sorgenti sismiche?
Può essere d’aiuto la geologia?
Sono disponibili indicazioni
indicazioni assai deboli che
per di più riguardano solo
le faglie che raggiungono la
superficie
Un censimento di questo tipo rischia si essere per lo
meno incompleto
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Si preferisce allora rinunciare alla ricerca delle faglie singole cercando
almeno di identificare zone potenzialmente sismogeniche nelle quali ci
si aspetta che i meccanismi di generazione dei terremoti (tipo di faglia
faglia,
tasso di deformazione) sia omogeneo
Si parte da modelli a larga scala (più o
meno condivisi) e si ripartisce il territorio in
zone ritenute omogenee (zonazione
sismotettonica): all’interno di queste zone i
t
terremoti
ti possono localizzarsi
l
li
i ovunque
con la stessa probabilità
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Il problema peggiore riguarda però il “quando” del terremoto
Carico tettonico
Attrito statico
Il modello più semplice è quello
illustrato di fianco (modello del
“ciclo sismico”
L entità della deformazione
L’entità
complessivamente accomodata dal
terremoto (la dislocazione sismica)
rimane costante
In presenza di un tasso di deformazione
costante il ciclo sismicosi ripete
costante,
Secondo questo modello, una struttura
sismogenica appena attivata dovrebbe
rimanere quiescente e risultare quindi
non pericolosa per molti anni
La Pericolosità Sismica – D.Albarello
T
Terremoto
t
Attrito dinamico
Tutto molto semplice:
peccato che non
p
funzioni!
Non c’è nessuna parte
d l mondo
del
d nella
ll quale
l
un ciclo del genere sia
stato osservato!
20 Febbraio 2013 – h.16.00‐17.00
In realtà, più studiamo i terremoti e meglio si vede che :
•
I terremoti
t
ti esibiscono
ibi
una natura
t
essenzialmente
i l
t stocastica
t
ti
che non dipende da una maggiore o minore accuratezza
delle misure: in pratica hanno un carattere essenzialmente
irregolare
•
Le eventuali regolarità (persistenze) vanno cercate a livello di
proprietà della popolazione e non sui singoli eventi
Per esempio si vede che il numero di
terremoti decresce regolarmente (ed allo
stesso modo ovunque) con la
magnitudo: i terremoti molto intensi sono
assai più rari dei terremoti deboli
(“Legge di Gutenberg e Richter”)
Tutto questo ha scoraggiato un
approccio di tipo deterministico alla
previsione dei singoli terremoti a
favore di approcci di tipo
probabilistico
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Cosa è modello statistico/probabilistico?
Il processo (per esempio quello sismogenico) è modellato come un
congegno (di struttura interna ignota) che fornisce come esiti (“output”)
eventi sismici distribuiti nel tempo in modo che nessun evento sia di per
sé prevedibile
Black-box
tempo
Un tipo di processo del genere è detto processo stocastico e può essere
costruito matematicamente a partire da un certo numero di vincoli o
condizioni assai semplici
Quanto più questi vincoli sono simili a quelli effettivamente operanti nel
processo reale che si vuole rappresentare, tanto più la popolazione teorica
risultante risulterà simile a quella che si vuole studiare
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Nel caso del processo sismogenico i vincoli sono:
1. Gli eventi (intesi come superamento al sito di una data
soglia di scuotimento) sono relativamente rari (la probabilità
di due eventi simultanei è nulla)
2. Gli eventi avvengono indipendentemente l’uno dall’altro (in
pratica dall’occorrenza di un evento oggi nulla si può dire
sulle future occorrenze))
3. Il processo sismogenico è stazionario (ovvero un
qualunque intervallo temporale scelto a caso presenta
caratteristiche identiche dal punto di vista statistico)
In termini di modellazione statistica un processo di questo
tipo è detto Poissoniano
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Il modello poissoiniano è controllato da un solo parametro λ che premette
di rappresentare l’intero processo
l è il numero medio
di di eventi
ti che
h il congegno genera nell’unità
ll’ ità di ttempo
Questo parametro può essere stimato per via empirica a partire dalle
realizzazioni del p
processo,, contando gli
g N eventi che in un tempo
p ∆T sono
generati dal “congegno”
In questo caso
N
λ=
∆T
L’inverso di λ è detto tempo
medio di ritorno
∆T
T =
=
λ
N
1
Importanti proprietà del processo di Poisson
1.
Un solo parametro basta a caratterizzare l’intero processo
2.
Il tempo medio di ritorno (λ-1) non è il tempo di inter-evento
più probabile
3.
Visto che le probabilità sono più alte per in tempi di interevento più brevi, gli eventi prodotti dal processo non si
distribuiscono uniformemente nel tempo ma tendono a
concentrarsi
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Utilizzando questo modello, a partire da un valore del
parametro λ è possibile per esempio rispondere alla
domanda:
Qual è la probabilità P che in un intervallo di lunghezza ∆t
(t
(tempo
di esposizione)
i i
) sii abbia
bbi almeno
l
un evento
t con
scuotimento superiore a A
P ( A) = 1 − e
− λ∆t
≈ λ∆t
Infatti, variando a piacere A posso valutare la diversa
verosimiglianza degli scenari possibili (ovvero dei
diversi valori di A)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Per fare un esempio:
Supponiamo che ci interessi la probabilità che al sito si verifichi
almeno un terremoto con scuotimento con valore di PGA pari a
0.01g in un futuro intervallo di 50 anni
Dalla storia sismica passata sappiamo che un tale evento è
avvenuto due volte in 150 anni
Allora
2
= 0.013
λ=
150
Quindi
P(0.01) = 1 − e
La Pericolosità Sismica – D.Albarello
− λT
= 1− e
−0.013⋅50
= 0.48 = 48%
20 Febbraio 2013 – h.16.00‐17.00
VIII MCS
Un altro esempio
3
= 0.008
λ (VIII ) =
380
P(VIII ) = 1 − e
La Pericolosità Sismica – D.Albarello
− λT
= 1− e
−0.008⋅50
380
T (I 0 ) =
= 127 y
3
= 0.01
20 Febbraio 2013 – h.16.00‐17.00
VIII MCS
Un altro esempio
3
780
= 0.004 T =
λ=
= 260 y
780
3
P(VIII ) = 1 − e − λT = 1 − e −0.004⋅50 = 0.004
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Posso eseguire
g
il calcolo p
per vari valori di scuotimento ((A)) ed
ottenere così diversi scenari di scuotimento a ciascuno dei quali è
associato un valore di verosimiglianza (probabilità)
Ciascuna di queste curve è detta curve di pericolosità che
forniscono per ogni valore di scuotimento la relativa
verosimiglianza
g
Naturalmente
esistono curve
diverse per i
di ersi tempi di
diversi
esposizione ∆t
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Avendo a disposizione le curve di pericolosità P(A,∆t) sarebbe per
esempio possibile stabilire un limite superiore ragionevole per lo
scuotimento sismico atteso nell’intervallo di esposizione ∆t
Questo limite può essere trovato rispondendo
rispondendo, per esempio
esempio, alla
domanda:
“Qual
Qual è il valore di scuotimento che ha una probabilità uguale al
10% di essere raggiunto o superato?” (Terremoto di riferimento)
Naturalmente per stimare il terremoto di riferimento bisogna avere
preventivamente calcolato P(A,∆t)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Scegliere come terremoto di riferimento quello che ha una probabilità di
essere superato inferiore al 10% in 50 anni corrisponde ad identificare il
terremoto caratterizzato da un tempo medio di ritorno pari a 475 anni
Infatti si ha che
P(I 0 ) = 1 − e −λ∆t → λ = −
T =−
∆t
1
log(1 − P(I 0 )) → T = −
∆t
logg(1 − P(I 0 ))
∆t
50
=−
= 475
log(1 − P(I 0 ))
log(1 − 0.1)
Si rammenti che questo non significa che questo terremoto tende a
verificarsi ogni 475 anni!! (sarebbe in contrasto con il carattere causale
degli eventi)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
In linea di principio, per fare tutto questo mi basterebbe conoscere λ
a partire dalla storia sismica del sito che intendo studiare
In pratica, devo conoscere gli eventi che, in un intervallo di tempo
adeguatamente lungo, hanno interessato il sito di interesse ai diversi
livelli di scuotimento
In realtà, qualcosa di simile è possibile nelle località dove la
documentazione sui terremoti del passata è assai estesa (come nel
caso delle maggiori e più antiche città italiane) e se è di interesse
uno scuotimento espresso in termini di intensità macrosismica
Negli altri casi questo approccio “diretto”
diretto risulta poco vantaggioso
In questi casi, bisogna utilizzare un approccio di tipo “indiretto” che
tragga vantaggio da tutte conoscenze disponibili: sia quelle di tipo
sismologico che geologico
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Si è detto che il problema centrale è quello di determinare λ ovvero il
numero medio di terremoti che nell’unità di tempo hanno superato
una determinata soglia A
Si presume che attorno al sito esista un certo numero di potenziali
sorgenti sismiche
Sito
Nell’unità di tempo, ciascuna sorgente i-ma è in grado di generare
mediamente una certa quantità di terremoti per una data classe di
magnitudo
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Sito
Data
D
t lla di
distanza
t
d
dall sito,
it solo
l una ffrazione
i
νi di d
deii
terremoti generati dalla singola sorgente sarà in grado di
provocare uno scuotimento almeno pari a A
Se esistono M sorgenti, allora si avrà che
M
λ = ν 1 + ν 2 + Kν M = ∑ν i
i =1
Il problema è allora quello di calcolare i valori νi
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Le magnitudo che interessano sono quelle capaci di generare al sito
di studio scuotimenti almeno pari a A
Per conoscere q
qual è q
questo valore di magnitudo
g
utilizziamo le
leggi di attenuazione nella forma che abbiamo già incontrato
A = 10
a + bM − log
(h
2
+r 2
)
Mediante questa relazione è possibile definire, per quella sorgente,
posta ad una distanza r dal sito, q
p
quale magnitudo
g
è in g
grado di
provocare scuotimenti almeno pari a Io al sito sotto esame
log A − a − log h 2 + r 2
M0 =
b
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
A questo punto, per sapere quanti eventi generati dalla sorgente
i-ma nell’unità di tempo possono interessare il sito con uno
scuotimento almeno pari a A, basta sapere quanti eventi con
magnitudo almeno pari a Mo questa sorgente è in grado di
generare nell’unità di tempo
A questo scopo è possibile utilizzare un catalogo storico per
identificare il numero µ di terremoti che in un tempo passato di
durata ∆T sono stati g
generati dalla sorgente
g
i-ma p
per la soglia
g di
magnitudo M0
Si avrà allora che
νi =
µ
∆T
Il problema è quindi spostato dal sito alla sorgente
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Riassunto del metodo di Cornell
a
b
a)
Definisco le sorgenti su
base sismotettonica
b)
Definisco per ciascuna
zona il tasso di eventi per
ciascuna classe di
magnitudo
c)
Definisco per ciascuna
zona la legge di
attenuazione
d)
Stimo il tasso di
occorrenza per classi di
scuotimento al sito
e)
Definisco delle curve di
pericolosità ovvero stime
le probabilità relative a
ciascun valore di
accelerazione
c
d
(from Algermissen & Perkins 1976)
La Pericolosità Sismica – D.Albarello
e
20 Febbraio 2013 – h.16.00‐17.00
La forma della carta è fortemente
condizionata dalla zonazione
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
PGA
La Pericolosità Sismica – D.Albarello
PSA ((1 sec))
20 Febbraio 2013 – h.16.00‐17.00
Le mappe precedenti sono tutte state espresse in forma di PGA
In realtà nulla vieta di costruire mappe relative al valore di
accelerazione p
per una determinata frequenza
q
A questo scopo basta tornare alle leggi empiriche di attenuazione ed
utilizzare i coefficienti relativi allo specifico valore della frequenza
In questo modo è possibile ottenere curve di pericolosità diverse per
le diverse ordinate spettrali
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Mettendo assieme tutti questi valori otteniamo il cosiddetto
Spettro a probabilità Uniforme
Questo spettro rappresenta per ciascuna frequenza, il valore di
ampiezza
p
della risposta
p
corrispondente
p
ad una p
probabilità di
eccedenza (10% per esempio)
NON E’ LO SPETTRO DI UNO SPECIFICO TERREMOTO!
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Questi spettri sono stati poi riportati ad una forma “standard” che
può
ò essere descritta
d
i con pochi
hi parametrii
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Sono quindi questi spettri a probabilità uniforme (che cambi a seconda
della probabilità di eccedenza scelta o del tempo di ritorno) alla base dello
spettro di riferimento semplificato fornito dalla normativa
Dalla forma di questi spettri vengono
infatti dedotti i tre parametri riportati
nell’allegato
nell
allegato B delle NTC del 2008
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
E’ la forma riportata nell’Eurocodice8 e nelle
NTC08
F0= valore che modifica la forma
spettrale
p
attorno al massimo
dello spettro in accelerazione
orizzontale
picco di accelerazione del
ag: p
moto del suolo sul piano
orizzontale (o PGA) espresso
in frazioni dell’accelerazione di
gravità
TC*: Periodo del tratto dello
spettro a velocità costante
dello spettro
Mentre η dipende solo dallo smorzamento
adottato per i terreni (comunque maggiore
di 0.55)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Possibili prodotti
1 Probabilità al sito S che lo scuotimento superi un certo
1.
valore Y in 50 anni
2. Scuotimento con una p
probabilità fissata (p
(p.es. 10%)) di
non superamento in 50 anni (terremoto atteso)
3. Per ciascuna frequenza, livello dello scuotimento che
in 50 anni ha una probabilità fissata (p.es. 10%) di non
essere superata (spettro a probabilità costante)
4 Terremoto di Progetto ovvero il terremoti di riferimento
4.
da utilizzare nelle simulazioni
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Quest’ultima informazione può essere ottenuta attraverso la
cosiddetta disaggregazione
Il punto di partenza è l’equazione
l equazione che lega il tasso di
superamento della soglia di intensità al sito A ai tassi di
sismicità nelle diverse zone sismogeniche è
M
λ = ν 1 + ν 2 + Kν M = ∑ν i
i =1
Sito
Sit
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
I contributi νi saranno in genere diversi e proverranno da varie
combinazioni
bi
i i di
distanza-magnitudo
t
it d (il colore
l
più
iù scuro iindica
di i
contributi maggiori)
Disttanza
Massimo
contributo
Magnitudo
g udo
Quella particolare combinazione di magnitudo e distanza permette di
identificare il terremoto più pericoloso al sito di interesse; questo terremoto
potrebbe essere preso in considerazione per le simulazioni
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
In sintesi
Le carte di pericolosità sismica sono costruite sulla base di una
approccio statistico/probabilistico nel quale il ruolo delle informazioni
geologiche è di fatto marginale
Sono tre le basi informative essenziali:
1. il catalogo sismico ovvero l’elenco dei terremoti noti fino al passato più
remoto
2. La geometria delle zone in grado di produrre i terremoti (zone
sismogenetiche o sismogeniche)
3. Le leggi di attenuazione per stimare lo scuotimento in un dato sito
Di fatto la carta è figlia di queste informazioni e nell’assunzione che
1. il processo che genera i terremoti sia costante nel tempo (stazionarietà)
2. le informazioni disponibili siano rappresentative di tutto quanto può
succedere in futuro (completezza)
3. gli eventi siano fra loro indipendenti (poissonianità)
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
In verità nessuna di queste assunzione ha una base fisica che ne
garantisca la validità: al contrario abbiamo forti indicazioni che
contrastano queste assunzioni
1. I tempi necessari a “ricaricare” una faglia sono dell’ordine delle centinaia
o migliaia
i li i di annii a ffronte
t di una catalogo
t l
sismico
i i di un migliaio
i li i di annii
al massimo (realisticamente solo soddisfacente dal 1600 in poi e solo
per la sismicità più intensa)
2. I terremoti non sembrano caratterizzati da stazionarietà: anzi tendono a
raggrupparsi sia spazialmente che temporalmente
3 Questo implica anche una forte dose di interazione fra i terremoti: ma se
3.
l’uno influenza l’altro l’ipotesi si Poissonianità sembra poco sostenibile
Di fatto le carte di pericolosità cominciano solo ora ad essere
“ lid t ” ovvero valutate
“validate”
l t t a posteriori
t i i in
i rapporto
t alle
ll “previsioni”
“
i i i”
effettuate (e le verifiche non sembrano fornire risultati
incoraggianti)
Tutte queste considerazioni e la necessità di aggiornare
continuamente le informazioni di base (per esempio le leggi di
attenuazione) rendono le carte di pericolosità un oggetto tutt’altro
che fuori discussione e definitivamente consolidato
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Nel sito INGV
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Selezionando
questo parametro
E la cella di
i t
interesse
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Si ottengono le curve di
pericolosità (espresse in
forma del parametro λ
corrispondente a diversi
valori di accelerazione)
Mediante questo valore
è possibile risalire alle
diverse probabilità per i
differenti tempi di
esposizione
P(m ) = 1 − e − λ∆t ≈ λ∆t
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Selezionando
questo parametro
E la cella di
i t
interesse
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00
Valori “Medi”
La Pericolosità Sismica – D.Albarello
numero di deviazioni
standard per cui un dato valore di
scuotimento (logaritmico) devia da
quello mediano predetto dalla
legge di attenuazione data una
coppia M-R
20 Febbraio 2013 – h.16.00‐17.00
Selezionando
questo parametro
e questo
parametro
t
Ordinate spettrali per periodi fissati
La Pericolosità Sismica – D.Albarello
20 Febbraio 2013 – h.16.00‐17.00