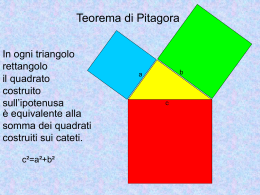
LA GEOMETRIA NELLA STORIA
E NELLA VITA REALE
Un percorso nell’antico Egitto e un
ritorno ai tempi moderni.
Annalisa Luongo Maria Paola Marino
I GEOMETRI EGIZIANI E LE TERNE
PITAGORICHE
TI SEI MAI CHIESTO COME GLI
ANTICHI EGIZI HANNO POTUTO
COSTRUIRE CON PRECISIONE UN
ANGOLO RETTO????
E ANCORA
LO SAI PERCHÉ LA TERNA DEI NUMERI 3, 4 e 5
E’ STATA CONSIDERATA SACRA?
LA TERNA E’ AVVOLTA DAL
MISTERO ……….
IN REALTA’…..
La terna 3,4 e 5 serviva per costruire con
precisione un angolo retto!
COME?
Ora te lo spiego
I “geometri” egiziani per costruire l’angolo retto: prendevano
una fune di una certa lunghezza, chiusa a mo’ di collana, divisa
in dodici parti uguali mediante nodi, poi fissavano a terra la
fune tendendola per bene (per questo i geometri venivano
chiamati “tenditori di funi”) con tre pioli posti in
corrispondenza di tre nodi in modo tale da formare un triangolo
i cui lati misuravano rispettivamente 3,4 e 5.
La terna 3,4,5 ha una caratteristica comune, nota fin
dall’antichità.
32+42=52
Dicesi terna pitagorica qualunque terna di numeri
naturali che sono le misure dei lati di un triangolo
rettangolo. ll quadrato del più grande è uguale alla
somma dei quadrati degli altri due.
25
16
9
PRECISAMENTE ….
•
•
Rispetto a una qualsiasi unità di misura tale terna rappresenta le misure dei lati
di un triangolo che è necessariamente rettangolo;
La somma dei quadrati delle due misure più piccole è uguale al quadrato della
misura più grande.
Interpretiamo la seconda proprietà da un punto di vista geometrico.
Assumiamo come unità di misura il cm. e osserviamo che:
32=9cm2
rappresenta l’area del quadrato costruito
sul cateto minore.
42=16cm2
rappresenta l’area del quadrato costruito
sull’ipotenusa cateto maggiore.
52=25cm2
rappresenta l’area del quadrato
costruito sull’ipotenusa
•
Geometricamente tale proprietà ci dice:L’area del quadrato sull’ipotenusa è
uguale alla somma delle aree dei quadrati costruiti sui due cateti.
CHI E’ PITAGORA?
• Certamente Pitagora è famoso
soprattutto per il suo TEOREMA: il
quadrato costruito sull'ipotenusa è
equivalente alla somma dei due
quadrati costruiti sui cateti.
• Ma come fece Pitagora a scoprire
questa relazione?
• CHISSA’ SE E’ STATO ISPIRATO DAGLI
ANTICHI EGIZI…..
IL TEOREMA DI PITAGORA
IL TEOREMA DI PITAGORA ASSERISCE :
In un triangolo rettangolo il quadrato
costruito sull’ipotenusa è uguale alla
somma delle aree dei quadrati costruiti sui
due cateti.
Q3 = Q1 +Q2
Q1
Q2
ORA TOCCA A TE!
• Prova a trovare altre terne pitagoriche e
riproduci in laboratorio l’esperienza dei
geometri egiziani.
HAI BISOGNO DI:
• Una fune.
• Un pannello di legno o di sughero su cui
fissare la fune.
• Spilline.
DIMOSTRA IL TEOREMA DI PITAGORA
CON METODO DELLA PESATA
•
•
Disegna un triangolo rettangolo e i tre quadrati costruiti sui tre lati su uno stesso cartone
di spessore uniforme.
Ritaglia i tre quadrati
•
Poni il quadrato costruito sull’ipotenusa
su uno dei bracci della bilancia.
•
Poni i due quadrati costruiti sui cateti
sull'altro braccio della bilancia.
LA BILANCIA E’ IN EQUILIBRIO PERFETTO!!!
Calcolo di altezze non
misurabili
Come calcolare l’altezza di una
piramide con un bastone
UNA DOMANDA DIFFICILE:
Puoi calcolare l’altezza di
una piramide con un
semplice bastone ?
CHISSA’ QUANTI ANNI DI
STUDIO DI MATEMATICA
DOVRAI FARE PER
RISPONDERE A QUESTA
DOMANDA …….
SORPRESA!
ANCHE UNO STUDENTE DI SCUOLA
MEDIA E’ IN GRADO DI DARE LA
SOLUZIONE.
BASTA CONOSCERE LE PROPORZIONI!
Osserva questo disegno.
E’ una piramide retta a base regolare.
I triangoli rettangoli ABH e A’B’H’ sono simili per il I criterio di
similitudine dei triangoli.
I lati corrispondenti sono in proporzione, ossia
x:A’H’=HB:H’B’
dove:
x è l’altezza della piramide;
A’H’ è l’altezza del bastone;
H’B’ è l’ombra del bastone sul terreno;
HB è la somma del segmento BC e della metà dello spigolo di base
della piramide.
Pertanto
ORA TOCCA A TE!
• Ripeti i criteri di similitudine dei triangoli
con Cabri
• Ricerca su Internet altre applicazioni che
utilizzano i criteri di similitudini dei
triangoli.
ANCORA
• Misura l’altezza di un oggetto (un palazzo, un
albero….) con un bastone.
HAI BISOGNO DI:
Un bastone.
Un oggetto.
Una bella giornata di sole.
Ricorda che l’oggetto prescelto deve trovarsi in una zona
pianeggiante per riuscire a individuare correttamente la
sua ombra.
BUON LAVORO