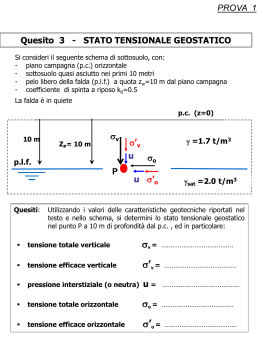
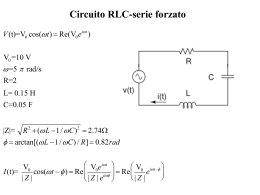
PARTE I
Esercizio 1 - Temperatura di un RTD noti
corrente e tensione
Calcolo la resistenza come TENSIONE/CORRENTE, ottengo un valore
Resistenza dell'RTD è anche uguale a R0 + R0 a T = 100 + 0.4 x T
(R0 e R0a sono costanti rispettivamente a 100 ed a S=R0a=0.4)
quindi eguaglio 100 + 0.4 x T al precedente valore e dalla semplice
equazione mi ricavo la temperatura.
Esercizio 2 – Termocoppia ed RTD
Una termocoppia K
Presenta una d.d.p al giunto freddo Vacq = 3.297 mV
La temperatura del giunto freddo viene rilevata mediante un sensore
RTD Pt100
Per la trasduzione della resistenza RTD si usa un P. di Wheatstone
bilanciato a 0 gradi, con Rs = 100 Ohm ed R= 24 kOhm
Tale ponte fornirà una tensione in uscita pari a E(TF) = 7.967 mV
(quindi a questa tensione non è bilanciato)
Per una tensione di alimentazione VAL = 24V
Approssimando la sensibilità di RTD a 0.4
Determinare le temperature dei giunti caldo e freddo di tale
termocoppia
1)
Faccio ipotesi di linearità dell'uscita dell'RTD su ponte di
ST
Wheatstone Tensione = KT = R0  R VAL
2)
Ho tutti i dati della precedente formula quindi ottengo che la
temperatura a cui è sottoposta l'RTD, ergo la temperatura del giunto
freddo della termocoppia è T = circa 20°
3)
Faccio la compensazione E(Tc, 0) = Vacq + E(Tf, 0)
4)
Vacq sarà la d.d.p al giunto freddo che ho già
5)
E(Tf, 0) sarà presa da una tabella in dotazione vedendo l'uscita E
ai 20° che mi sono appena calcolato
6) 3,297 + 0,798 = 4.095
7)
Dalla tabella si ricava che tale temperatura equivale a 100°, quindi
la soluzione è (20°,100°)
8)
Nell'ipotesi in cui io non avessi avuto i 20° in tabella (e quindi avrei
dovuto avere la tensione corrispondente), avrei dovuto fare un
procedimento di interpolazione per tensione incognita:
V =V1
V2 −V1
T −T1
T2 −T1
Se invece avessi avuto una tensione risultante al di fuori della tabella,
avrei dovuto usare la stessa esatta formula di interpolazione, ma
sostituendo tensioni con temperature e viceversa
Esercizio 3 – Variazione contemporanea di
due celle capacitive
Ho un ponte di Wheatstone da come sopra:
R = 1000 ohm
C1 = C2 = 800 pF
VAL = 5 seno (2 π 10 alla quarta t)
Calcolare l'ampiezza della sinusoide in uscita dal ponte di Wheatstone
se C1 aumenta del 10% e C2 del 10%
C1 E C2 DIVENTANO 880 E 720 per definizione nella traccia
E = Va – Vb
Prima cosa trovo Va e Vb tramite una formula di calcolo tensione di
potenziali ponte di Wheatstone
E =
Ra
Rx
 VAL
Ra  Rb Rx Rc
Ra
VAL=VA
Ra  Rb
Rx
VAL=VB
Rx Rc
fatto nel dominio di Laplace (si sottintende s = jω). 1/SC1 è
semplicemente la trasformata dell'impedenza del condensatore
1
sC 1
1
Va=
VA L s=
V AL s
1
1sRC 1
R
sC 1
1
sC 2
1
Vb=
VA L s=
V AL s 
1
1sRC 2
R
sC 2
1
1
−
VAL  s
1 sRC1 1sRC2
1
1
E =
−
VAL  s
1  jomegaRC1 1  jomegaRC2
E =
Senza riportare qui tutti i calcoli, ω ce l'ho, è lo stesso della tensione di
alimentazione ovverossia 2 π 10 alla quarta.
Risolto ciò, dovrò fare modulo e fase del numero complesso che otterrò
(senza VAL però, che va messo sotto l'input, in maniera tale da ottenere la
funzione di trasferimento), ed il risultato di tutto l'esercizio sarà quindi:
Sinusoide = Modulo * Modulo ingresso ( 2 π 10 alla quarta + fase)
Il modulo dunque è l'ampiezza massima della sinusoide.
Esercizio 4 – Accelerazione e spostamento
in uscita ad un accelerometro:
Ho un accelerometro:
− Sensibilità: 6mv/metri al secondo al quadrato
− Frequenza naturale: 5 Khz
− Smorzamento: 0.1
− Funzione di trasferimento:
−
−
Dove ω n = 2 π frequenza naturale quindi 2 π 5 x 10 alla terza (non
confondere pulsazione con frequenza. In generale la pulsazione
dovrebbe essere una velocità angolare di un fasore rotante, ed è la
frequenza della sinusoide moltiplicata per 2 π)
Se tale accelerometro è sottoposto ad una vibrazione di frequenza
100 Hz (e quindi x''m = am = accelerazione della massa sismica =
A sin (2 π 100 t)
(è ovvio che ci sia “t” perchè è una grandezza periodica nel tempo)
Si ha in uscita una tensione picco-picco di 2,4 V
−
Trovare l'ampiezza dell'accelerazione e dello spostamento cui è
sottoposto l'accelerometro (l'ampiezza è il valore massimo della
sinusoide ergo anche il modulo del relativo fasore. La fase
ricordiamolo invece è lo sfasamento rispetto ad una sinusoide
perfetta)
1)
Calcolo A cioè l'ampiezza dell' accelerazione =
Tensione/Sensibilità = 2,4/0.006 = 2400/6 = 400 metri al secondo
al quadrato
(da qui si può dedurre la formula universale uscita/ingresso = sensibilità, per cui noto un
uscita od un ingresso e la sensibilità è facile dedurre l'altro)
2)
xr sarà in forma Xr sen (2 π 100t + Beta)
(da qui invece si può dedurre che la frequenza ereditata dallo spostamento relativo,
e probabilmente anche in quello globale, è quella applicata. Però c'è uno
sfasamento perchè lo spostamento è appunto relativo)
1
d
k
2
s  s
m
m
3)
Se W(s) =
4)
Inoltre = • 2SmorzamentoPulsazione = d/m
• Pulsazione al quadrato = k/m, quindi:
W(jω) =
1
2
ω 2 smorzamentoωn j ωωn
2
in cui è sottinteso che ω uguale 2 π 100
5)
A questo punto sono rimasto con lo scopo di calcolare lo
spostamento. In qualche modo:
Modulo dello spostamento =
Modulo accelerazione X Modulo funzione
questo si può intuire tipo dal fatto che la funzione di trasferimento impone che lo
spostamento sia l'uscita e l'accelerazione l'ingresso. Infatti ricordiamo l'esempio detto
sopra sulle risposte in frequenza e sulle funzioni di trasferimento con le sinusoidi:
Se Acos(ωot) e’ il segnale in ingresso a un sistema con risposta in
frequenza G(jω), l’uscita e’
A| G(jωo)| cos(ωot+Φ(ωo))
Fase dello spostamento = Fase della funzione di trasferimento
Dunque, premesso che:
Am = (Tensione/Sensibilità) = 400
Xr grande = Am x Modulo W(ω)
Beta = Fase W(ω)
400 moltiplicato (MODULO W(ω)) sen 2 π 100t + (FASE W(ω))
Esercizio 5 – Calcolo costante di molla e
coefficiente attrito viscoso di
accelerometro:
Un accelerometro ha:
− Massa sismica 100 grammi
− Smorzamento 0.1
− Banda passante [0, 100] Hz
− Sensibilità S = 0,8 V/g
− Massimo valore misurabile 1,5 g
CALCOLARE K e D
1) Sappiamo le relazioni tra K, D, smorzamento e frequenza, ovvero:
2)
Inoltre so che
3)
Che diventa
4)
Prendendo dalla precedente formula di ω, ho che:
5)
Vado a mettere tale quantità nello smorzamento e ottengo che:
d
d
m
m
d
Sm orzam ento=
=
=
2
om
ega
m
2
om
ega
m om egaquadro
2
m

da cui, prendendo primo ed ultimo membro e facendo semplice
equazione ho che d = smorzamento m 2 ω
CALCOLARE Am e xr sapendo che
- am = Am sen (2 π 10 t)
- in uso v(t) = 1,2 sen (2 π ω t + 4)
Am sarà uguale a Tensione su Sensibilità = 1,2/0,8 = 3/2 = 1.5 g
La funzione di trasferimento W in (2 π 10 = s) è
1
2π 10  2 smorzamento ωn j 2 π 10 ωn 2
2
Da cui, visto che W = Xr / Am, come si può vedere nelle precedenti
slide (in cui Am è chiamato X'')
Per ottenere Xr mi basterà moltiplicare tutto il suddetto per Am
Esercizio 6 - Ponte estensimetrico con
amplificatore:
Ho un ponte estensimetro che viene usato per una misurazione.
Questa tensione viene amplificata da un amplificatore
Range di deformazione dell'estensimetro: Dl/l = 5 moltiplicato 10
alla terza milliE (quella è stramba in alto)
− Il gain factor è 2
− Val = 5V
−
Calcolare il guadagno in modo tale che l'uscita sia compresa tra [- 10V
e 10 V]
1)
Cambio da milliE ad E
2)
Valuto dal ponte, E+ ed E-
3)
Ho che la tensione di uscita del ponte è pari a
VA – VB
4) Applico la formula del calcolo tensione del ponte:
5)
Tensione quindi è compresa tra [- 0,05 e + 0,05], e per calcolare
invece il guadagno con la tensione compresa tra [-10 e 10] non
devo far altro che dividere
Tensione che voglio
Tensione che ho
= 200, che poi sarà uguale al rapporto
amplificatore differenziale
R2
R1
di un
Esercizio 7 – Potenziometro dimmer
(anche se nell'IMG non si vede bene, le resistenze sopra e sotto sono tutte RE)
PUNTO UNO, IPOTESI SENZA CARICO:
R1+R2 mi dà RP, resistenza del potenziometro visto che sono due
resistenze in serie.
Ho effettuato questa suddivisione di RP in modo da poter rendere R2 la resistenza che poi
sarà in carico con quella del carico quando lo andremo a calcolare. Dunque R1 sarà la
resistenza che all'aumentare del cursore diminuirà, mentre R2 aumenterà all'aumentare del
cursore
6)
Ho che R2 è la parte di resistenza sotto al “dimmer”, per cui R2 sarà
uguale a (X/L)RP
Quindi
R1 + (X/L) RP = RP
R1 = RP – (X/L) RP
R1 = ( (L – X)/L )RP
7)
Da cui, se non c'è il carico, secondo il partitore di tensione (dovrebbe
essere ovvio, alla fine è una semplice serie di resistenze, il problema
è che non lo risulta perchè il potenziometro è disegnato molto male e
non si capisce la sua struttura):
X
RP
R2
L
V0=
VAL=
VAL
RP  R E R E
2R ERP
8) Se invece il carico c'è:
R2 RL
R2  P A R RL
R2 RL
V 0=
V A L=
VAL
R1 R2  P A R RL R E  R E
R2 RL
2R ER1
R2 RL
Esercizio 8 – Fotoresistore con Ponte di
Wheatstone
1) Bilancio il ponte in modo tale che l'uscita sia 0 a 10 di illuminazione
2) Il ponte è bilanciato quando RL R1 = RL Rlux, ovvero quando R1 = Rlux
3) Quindi metto l'illuminazione al minimo, mi calcolo la resistenza tramite la
formula, e do a R1 lo stesso valore.
4) Inoltre mi calcolo VB con tale valore di R1
5) Quindi mi calcolo VA con il valore di illuminazione massimo, e calcolo
l'offset
6) Porto l'Offset a 10 tramite un guadagno calcolato da un amplificatore
differenziale ed ho risolto il congegno
Esercizio 9 – Condizionamento di un
sensore di posizione angolare
Domanda:
per rimuovere l'offset di tensione di 5.4V da quella globale del trasduttore
cosa ci metto nell'amplificatore differenziale?? La tensione del trasduttore
ed un generatore di tensione da 5.4V??? O un secondo trasduttore con
pendolo fermo?? Un esercizio può prevedere aggiunte del genere?
Risposta:
la soluzione è esattamente simile a quella dell'esercizio uscito ieri: un capo
dell'amplificatore lo colleghi al trasduttore e l'altro ad un partitore di
tensione con i valori delle resistenze e dell'alimentazione scelti in maniera
tale che su quella maglia ricada una tensione di offset di 5,4 volt
Esercizio 10 – Condizionamento di una
termoresistenza tramite generatore di
corrente costante
Come disegnato sul quaderno va bene???
E' giusta la formula del partitore di tensione così???
A cosa mi serve la tensione di alimentazione degli operazionali?
Esercizio 11 – Progettazione di filtro
passivo
− Si supponga di elaborare un segnale con una banda di 10 Hz
− A cui sovrappongo un segnale di 150 Hz
1) PROGETTARE UN FILTRO PASSIVO TALE CHE
L'ATTENUAZIONE del rumore SIA DI 20 DB
2) CALCOLARE LO SFASAMENTO IN CORRISPONDENZA
DELL'AMPIEZZA MASSIMA
1)
Calcolo a(ttenuazione), che sarà uguale a:
1
1
2 Pi Greco Disturbo =
2 Pi Greco 150 =2 Pi Greco 15
Decibel ∈logaritmi
10
(ricordiamo che i decibel/logaritmi seguono la corrispondenza 20db => 10, 40db=> 100,
ovvero ho che:
 db 
20
a=10
, che poi si dovrà mettere come denominatore del rumore, come precedentemente illustrato,
e riferirsi alle varie formule del filtro, come:
a=
1
RC
1=
b
b
W=
a
sa
2)
Inoltre se la tensione in uscita è dimezzata, allora T corrisponde a
-6dB, Se la potenza in uscita è dimezzata, allora T corrisponde a
-3dB.
3)
In sintesi: nel passare da una frequenza f ad una k volte più
grande, la risposta diminuisce di 20log10(k) dB. Se k=2, la risposta
diminuisce di circa 6dB: si dice che il filtro ad un polo garantisce una
attenuazione di 6dB per ottava, o anche (più raramente) di 20 dB
per decade.
4) Dunque 2 π 15 è approssimativamente 90, che sono i radianti al
secondo
5) Essendo come abbiamo visto per i filtri passivi del primo ordine
che b/a = 1, allora banda passante sarà uguale a 90
6) La funzione di trasferimento W(s) in s , essendo pari a b/a + s,
sarà uguale a 90/90+s
7)
A me però, visto che sono in corrente alternata, serve la risposta in
frequenza con
s=jω
ω = pulsazione di disturbo (quindi frequenza per 2 pi greco)
8)
Quindi riscrivo la funzione di trasferimento in frequenza
W ω  per ω=2 pi greco 150 =
9)
90
90  j 2 pi greco 150
Risostituisco 90 con 30 π per fare delle semplificazioni e ottengo:
10)
Ora mi servono modulo e fase della funzione di
trasferimento
(ricordiamo che il modulo e la fase della risposta armonica
caratterizzano il comportamento in frequenza del sistema: per
ogni fissata frequenza esprimono la modifica in modulo e fase
che subisce un segnale periodico puro nel transito attraverso il
sistema.)
11) Da
cui, si può stilare un piccolo diagramma di Bode delle fasi:
Infine, prendo il semplice 30 π che avevo prima, e lo sfrutto per creare il
mio filtro passa-basso tramite un circuito RC
Esercizio 12 – Coppia di un motore a
corrente continua
Assegnato un motore a corrente continua con:
R = 2 Ohm
Kt = 1,2 Nm/A
Vminx = 120 V
Supposto che il motore giri ad una velocità di 900 rpm = visto che sono
giri al minuto sarebbe 900 * π su 60 = 30 π
- Calcolare la coppia massima erogata dal motore.
Ho semplicemente che
Cm =
Kt
1.2
Vi Ke Velocità =
120 −1.2 Moltiplicato 30 pi greco =risultato numerico
Resistenza
2
Esercizio 13 - convertitore
tensione/corrente
Un sensore di temperatura S, realizzato con materiale semiconduttore,
produce in uscita una corrente proporzionale alla temperatura.
Nelle applicazioni pratiche si pone il problema di convertire il segnale di
uscita dal sensore in una tensione adattata tipicamente alle specifiche dei
convertitori ADC.
Tra i possibili circuiti di conversione corrente-tensione si consideri il
seguente:
Nell'ipotesi che:
1) Il sensore di temperatura S presenti una caratteristica I = KT con K
= 1 microAmpere/°C
2) Il convertitore I/V fornisca all'uscita un livello di tensione Vout
compreso tra 0 e 5V per variazioni di temperatura tra 20 e 50 gradi e
per una TENSIONE DI ALIMENTAZIONE di 12 Volt
Dimensionare opportunamente le resistenze R1 ed R2 del convertitore
desiderato.
Svolgimento:
1) Abbiamo che, vista la caratteristica del sensore I = KT, devo
semplicemente moltiplicare la temperatura per un microampere ed
otterrò la corrente che esso emette a quella temperatura (così poi da
valutarne un condizionamento opportuno).
Quindi 10 alla meno sei per 20° = 20 microAmpere
Quindi 10 alla meno sei per 50° = 50 microAmpere
2) Vista la configurazione attuale ho che l'amplificatore, per definizione
definisce nel calcolo di correnti e tensioni la presenza di un corto circuito
virtuale, ovvero posso ridisegnare il circuito come:
, da cui risulta ovvio che Vout = R2 i2, dove i2 è la corrente che scorre
nel ramo di retroazione dell'amplificatore.
Mentre vista la resistenza virtualmente infinita vista in ingresso
nell'amplificatore ho che
i1+i2 = I
3) i1 = Val/R1 (normale rapporto corrente-tensione)
i2 = Vout/R2 (idem)
4) Per i dati del problema, ho che la temperatura a 20° produce una
tensione in uscita pari a 0.
Quindi per il rapporto tensione/corrente anche i2 sarà 0
I quindi è sostanzialmente i1
Quindi i1 = I a 20°, ovvero, come detto sopra 20 microAmpere
5) Quindi ancora, visto che i1 = VAL/R1
R1 = VAL/20 microAmpere = 12 V / 20 MicroAmpere =
= 3/5 * 10 alla 6 = 0.6 MegaOhm
6) Adesso usiamo T a 50° per calcolare R2
Quando la temperatura sale a 50 gradi, Vout, che è 5V, che abbiamo visto
essere R2i2
7) Se Vout = R2i2, allora i2 = Vout/R2 = 5V/R2
8) Prendendo dalla formula precedente ho che essendo I = i1 + i2, sarà
uguale a Val/R1 (che ormai ho) + 5V/R2.
R2 qui è l'unica incognita e risulta facile trovare il risultato
Esercizio 14 – Rete di trasduttori ed
amplificatori
1) Per verificare l'escursione del traduttore in Millivolt,
semplicemente moltiplico l'escursione del campo magnetico per la
variabile S
2) Ottengo i valori efficaci delle tensioni MIN e MAX semplicemente
dividendo per 2radical2
3) Vout sarà il semplice (Veff – Vref) R4/R3. Ho tutti i dati, posso
procedere al calcolo ed alla verifica
4) Punto 2 : La frequenza del segnale, come dice la traccia, è di
qualche centinaio di HERTZ
5) Per verificare se passa “bene” il segnale, devo verificare la
frequenza di taglio nell'atto del filtraggio, e devo verificare se sia
compatibile
6) La frequenza di taglio è semplicemente uno su due pi greco R
(quindi 150 kappaohm, come in figura), per C (quindi 10 alla meno sei
come in figura). Risultato ovvio
Formulario:
•Numeri complessi, corrispondenza coordinate polari / cartesiane:
a  jb=r cos θ  j r sen θ
•Modulo e fase di un numero complesso:
Modulo r=  a 2b 2
Fase θ =arctg b / a 
•Inverso di un numero complesso:
a
a∗com plessconiugat a
•Rapporto tra numeri complessi (si consideri sempre che j al quadrato è -1):
a
a
complessoconiugb
= ∗

b
b
complessoconiugb
•Trasformata di una derivata nel tempo di una funzione f(x):
s f x
•Trasformata di un integrale nel tempo di una funzione f(x):
f x
s
•Trasformata di un condensatore:
1
I  s
sC
•Trasformata di un induttore:
sLI  s 
•Funzione di trasferimento:
Out  s
Ing  s
•Risposta in frequenza:
W  s=W  jω
Modulo = guadagno in ampiezza del segnale in ingresso
Fase = sfasamento del segnale in ingresso
•Compensazione termocoppia:
•Resistenza di un termoresistore a temperatura T:
R(T) = R0(1+aT) = R0 + R0aT
oppure, se invece di avere R0 ho ad esempio R25°
R(T) = R25(1 + a(T - 25))
•Sensibilità di un termoresistore:
R0a
•Tensione in uscita da un Ponte di Wheatstone

3
4
−
VAL
3 1 24
•Tensione in uscita da un RTD condizionata tramite ponte
E=
ST
VAL
R0  R
•Interpolazione per fattori mancanti in tabelle di termocoppia
V =V1
V2 −V1
T −T1
T2 −T1
•Relazione caratteristica di un termistore
1
=AB log  R C log  R 3
T
•Relazione caratteristica di un manometro a colonna
p1 ∗Area = p2 ∗Area Densità ∗Area ∗ΔAltezza ∗Forza di Gravità
p1 − p2 =Densità ∗Δ Altezza ∗Forza di Gravità
•Cella Capacitiva
C =Costante Dielettrica Relativa ∗Costante dielettrica nel vuoto
Area
Distanza
•Cella Capacitiva condizionata con Ponte di Wheatstone
1
sC 1
1
Va=
VA L s=
V AL s
1
1sRC 1
R
sC 1
1
sC 2
1
Vb=
VA L s=
V AL s 
1
1sRC 2
R
sC 2
1
1
−
VAL  s
1 sRC1 1sRC2
1
1
E =
−
VAL  s
1  jωRC1 1 jωRC2
E =
•Variazione della resistenza in funzione della variazione dell'allungamento in un
estensimetro
ΔR=R −R0 R0 2R0
ΔL
L0
•Gain Factor di un estensimetro (è quasi sempre circa 2)
ΔR / R
ΔL / L
•Ponte di Wheatstone Estensimetrico
ε+ = R0 + ΔR
ε- = R0 – ΔR
Tensione in uscita =
=
VAL
ΔR
R0
VAL
R0  ΔR
R0 −ΔR
−VAL
R0 ΔRR0 − ΔR
R0 −ΔRR0  ΔR
(R0 o R è la stessa cosa)
•Sensore di pressione idrostatica:
Altezza liquido =
pressione fondo serb − pressione pelo libero
densità X gravità
•Potenziometro dimmer:
Tensione tra terminali mobili =VALimentazione
Lunghezza parziale X
Lunghezza totale L
•Accelerometro-massa-molla-smorzatore:
massa x accelerazione = fmolla  fsmorzatore
fmolla =coefmolla lunghtotale −distanzamassariferimento

fsmorzatore =coeattrito veltotale −velmassariferimento 
•Accelerometro-posizione relativa:
xrel =lunghtotale −distanzariferimento
xrel ' =veltotale −velmassariferimento
•Accelerometro-funzione di trasferimento:
Posizione relativ auscita
=L 
Accelerazioneingresso
Xr
x '' r
d
k
x ' r x r
m
m
•Accelerometro-pulsazione naturale:
•Accelerometro-smorzamento:
=
1
d
k
2
s  s
m
m
=
•Effetto di una capacità parassita C12 in un accoppiamento capacitivo
V2  s=
C2G
V1 s 
C12C2G
•Amplificatore in configurazione invertente
Resistenza ingresso = Ri
Nell'amplificatore non scorre alcuna corrente
Resistenza uscita = 0
Rapporto tensione/tensione = Vu = - Vi(Rf/Ri)
•Amplificatore in configurazione non invertente
Resistenza ingresso = infinito
Resistenza uscita = 0
Rapporto tensione/tensione = Vu = Vi(1+Rf/Ri)
•Amplificatore in configurazione differenziale
Ponendo Rg = Rf e R1 = R2
Rapporto tensione/tensione = Vu =
R2
v1−v2
R1
•CONNESSIONE differenziale tra amplificatori (tensione di nodo comune)
Vout = Guadagno(Vin +
tncmune
CMRR
)=
GdVin 
Gd ecm =GCM
CMRR
nell'ipotesi che l'impedenza in ingresso sia molto maggiore delle resistenze R1 ed R2,
e che l'impedenza del nodo comune sia infinita.
•Amplificatore da strumentazione
•Amplificatore in configurazione buffer
Vout =
Vin
Rc
Ra  Rc
•Circuito partitore di tensione
Vout =
R2
Vin
R1 R2
•Filtro primo ordine passabasso passivo
Funzione di trasferimento = W(s) =
b = banda
a = attenuazione
s = variabile complessa
b
=1
a
t =RC
1
=t
a
banda passante =[0,
!a !
] Hz
2π
b
sa
banda passante =[ 0,
1
] Hz
2π t
•Passaggio da attenuazione in decibel ad attenuazione “a”:
1
10

db

20
2 π Rum oreda attenuare
oppure un ottava per 6 decibel
•Filtro secondo ordine passabasso passivo
1
=R1C1
a1
1
=R2C2
a2
Funzione trasferimento:
Smorzamento=
b
s a1sa2
2
a1
2  a2
Pulsazionenaturale= a2
Con poli reali e quindi smorzamento positivo o uguale a 0:
Banda =[ 0,
! p1 !
]
2π
Con poli credo complessi e quindi smorzamento negativo:
Il filtro di second'ordine ha un'attenuazione di 40 db per decade, e 12 per ottava.
•Adattamento d'impedenza
•Convertitore corrente/tensione 1:
•Convertitore corrente/tensione 2:
•Filtro attivo passa basso invertente:
Guadagno = -R2/R1
Limite di banda = [0,
1
2πR2C
Guadagno = 1 + (R2/R1)
Limite di banda = [0,
1
2πRC
]
•Filtro a retroazione negativa multipla
V 0=
1
−Y1 Y3
Yx =
,
con
Zx
Y3 Y4 Y5 Y1Y2 Y3Y4 
•Filtro a retroazione positiva semplice
VOut =
1
Ra
Y1 Y4
Rb
, dove Ra/Rb = k
Vin = Y5 (Y1+Y2+Y3+Y4) + Y4(Y1+Y2(1-k)+Y3)
(e quindi la f.d.t è il rapporto di queste due quantità)
•Multiplexer (throughput):
Velocità di acquisizione (o t.put) = numero ingressi x frequenza campionamento
•Multiplexer (tempo di conversione):
T.d.c = somma dei tempi di commutazione + assestamento + conversione del
convertitore a/d
Deve essere minore del reciproco del throughput
•Campionamento di una sinusoide senza S&H (onde evitare problemi di
quantizzazione) :
1
Tempo di acquisizione necessariamente < 2numeringressi π f , con f frequenza del
segnale
1
Frequenza segnale necessariamente < 2numeringressi π ta , con ta tempo di acquisizione
•Codice binario uscente da un convertitore A/D
Codice =Intero 
Tensriferimento n 1
2  
Tensfondoscala
2
,
1
per Tensriferimento < Tensfondoscala * 1 2 n1
Codice=2 n−1
per Tensriferimento > o = Tensfondoscala *
1−
1
2
 n1
•Errore di quantizzazione di un convertitore A/D
Tensfondoscala/2^n
•Risoluzione di un convertitore A/D
100/2^n
•Rapporto risoluzione sensore/convertitore
1
mi serve un n di bit tale che 2n < R, risoluzione del sensore per unità quindi
n
2 
1
R
1

R
1
nlog10 2 log10  
R
n
log10  2 log10 
20∗n∗0,3 20∗log10 
1

R
(moltiplico entrambi per 20)
6n
1
dB
R
Quindi se ho la risoluzione in dB divido per sei ed ottengo un buon numero di bit del
convertitore
Se ho un numero di bit del convertitore moltiplico per sei ed ottengo la risoluzione in
dB necessaria per il sensore
•Convertitore a resistenze pesate
La resistenza raddoppia per ogni numero di bit
(2 bit = R e 2R)
(3 bit = R, 2R e 4R)
(etc.)
Vout =
±Vriferimento  n−1 
[2
∗Bit n−1]man manoa scendere fino a 1∗Bit0
2 n−1
•Convertitore R/2R
Ogni commutazione a 1 devia verso il ramo di uscita una corrente di peso
proporzionale al proprio
Soluzione a n = 3 bit (quindi non formula generica come nel convertitore
pesato):
−Vr
Rr
 n−1
∗
∗2
∗Bit n −1 si riduce a scendere fino ad arrivare a 1∗Bit 0
24
R
•Coppia rotante
t = Forza che agisce x dlunghezza spira proiettata sull'asse x
•Forza di Lorentz
F= Corrente * Vettore con direzione e verso della corrente e modulo uguale alla
lunghezza del conduttore (chiamiamolo L)* Campo magnetico
•Coppia rotante (deduzione)
t = Campo magnetico * L * Corrente * dlungspira
dlungspira = lunghezza spira per coseno dell'angolo theta che si forma
t = Campo magnetico * L * Corrente * lspira * cosTheta
•Coppia complessiva
tcomp = ∑ t per h da 1 ad N
quindi ∑ Campo magnetico ∗L∗Corrente ∗lspira ∗cosθ
quindi
Campo magnetico ∗L∗Corrente ∗lspira ∗∑ varicosθ
∑ varicosθ =k
Campo magnetico ∗L∗lspira = flusso
k ∗ flusso =Kt
da cui
tcomp = Kt * Corrente
•Forza elettromotrice
fem = L * Vettore velocità * Campo Magnetico
vettore velocità =velocità ∗sen 90 °θ 
fem = L * Velocità * Campo Magnetico * sen(90° + θ)
sen 90 ° Theta =cos θ 
fem = L * velocità * Campo Magnetico * cos(θ)
velocità =velocità angolare ∗lspira
fem = L * velocità angolare * lspira * Campo Magnetico * cos(θ)
Campo magnetico ∗L∗lspira = flusso
fem = flusso * velocità angolare * cos(θ)
Femcomplessiva = ∑
fem
Femcomplessiva = flusso * velocità angolare * ∑ cos θ 
∑ cos θ ∗ flusso = Ke
Femcomplessiva = Ke * velocità angolare ω
•Equazioni caratteristiche del motore brushed
Ke = Kt
V = RI + L di/dt + FEM
V = RI + FEM (a velocità costante Ldi/dt = 0)
Coppia = Kt I
Coppia (altra formula) = Ke ω + j ω + Cr
Coppia (a velocità costante) =
Kt
V − Ke∗velocità angolare 
R
Velocità a vuoto (velocità raggiunta dal motore in assenza di coppia di carico) =
V/Ke
Ke
Funzione di trasferimento =  sJ K e R L s K e Kt
•Motore Brushless (angolo elettrico)
angolo elettrico alfa = angolo elettrico theta * numero coppie polari
•Motore Brushless (potenza con tre fasi e coppia)
P (elettrica)= E1 I1 + E2 I 2 + E3 I 3, ma anche
P (meccanica)= Coppia X Velocità angolare
da cui,
Coppia =
E1 I1 E2 I 2 E3 I 3
Velocità angolare
•Motore Brushless Trapezio (flusso max)
Flusso max = Numero conduttori X Raggio Statore X Lunghezza assiale
rotore/statore X Integrale tra meno e più pi greco mezzi del campo magnetico = Primi
tre fattori uguali, mentre l'integrale è uguale al valore assunto dal campo magnetico al
traferro per pi greco
•Motore Brushless Trapezio (FEM indotta nella prima bobina)
FEM =
−derivata flusso
dt
FEM =
−derivata flusso
dtheta
∗

dtheta
dt
FEM =
−derivata flusso
∗ω
dtheta
Esprimendo quest'ultima formula in funzione del flusso massimo ho che la FEM
è un'onda quadra di ampiezza
2FlussoMassimo
∣ω∣
π
•Motore Brushless Trapezio (FEM indotta nelle due fasi in conduzione)
Forma trapezoidale di ampiezza pari a:
4FlussoMassimo
∣ω∣
π
•Motore Brushless Trapezio (Bilancio di potenza)
Coppia * ω = 2Ei Ii
•Motore Brushless Trapezio (Espressione della coppia)
Coppia =
2Ei Ii
FlussoMassimo
=8
I =Kt I
ω
π
•Motore Brushless Trapezio (Equazione caratteristica in caso standard)
Collegamento a stella quindi I1 + I2 + I3 = 0
•Motore Brushless Trapezio (Equazione caratteristica in caso di riluttanze
invarianti con l'angolo )
•Motore Brushless Generico (Funzione di forma generica della FEM)
E = omega Ki (Theta)
Con le Ki che variano (appunto, funzioni di forma)
•Motore Brushless Sinusoidale (Distribuzione sinusoidale di campo magnetico)
B(Generico Angolo di generico punto sul traferro, Angolo di rotazione del rotore) =
Ampiezza di B per coseno di (GADGPST - ARDR)
•Motore Brushless Sinusoidale (Conduttori contenuti in un angolo infinitesimo)
•Motore Brushless Sinusoidale (Flusso per spira costituita dai dn conduttori in
serie)
•Motore Brushless Sinusoidale (Forza controelettromotrice in spira costituita dai
dn conduttori in serie)
•Motore Brushless Sinusoidale (Forza controelettromotrice complessiva)
•Motore Brushless Sinusoidale (Funzioni di forma in caso di r coppie polari, ma
sempre tre fasi)
Fasi sfasate di due pigreco terzi
•Motore Brushless Sinusoidale (Forma da imporre alle correnti di fase)
•Motore Brushless Sinusoidale (Coppia risultante)
Tre mezzi p K I
PARTE II
• I 5 linguaggi
TESTO STRUTTURATO
LADDER DIAGRAM
DIAGRAMMA A BLOCCHI FUNZIONALI
LISTA ISTRUZIONI (ASSEMBLATIVO)
SFC
•Dichiarazione variabili (Testo strutturato)
Variabile1,Variabile2 : tipo
•Operatori (Testo strutturato)
x := 0
Gli altri come i booleani, aritmetici, etc., sono tutti fortemente intuitivi
•Costrutti di testo strutturato (selezione)
IF – THEN – END_IF
IF – THEN – ELSIF – THEN – ELSE – END_IF
CASE Variabile OF Valore : Istruzioni ELSE Istruzioni END_CASE
•Costrutti di testo strutturato (iterazione)
FOR Variabile = Valore TO Variabile = Valore BY Step DO Istruzione END_FOR
WHILE Condizione DO Istruzioni END_WHILE
•Contatti (ovviamente LD)
NA = Contatto standard di un rung in ladder
NC = Contatto negato di un rung in ladder
•Istruzione di salto (Ladder diagram)
---> Label
---<RETURN>--- (per uscire da un blocco)
•Spezzaggio di un rung (Ladder diagram)
--->LABEL> (vai)
>LABEL> (prosegui da)
•Istruzioni basso livello (Lista istruzioni)
ETICHETTA:(opzionale) OPERATORE OPERANDO
LD (Load)
ST (Store)
S (Set)
R (Reset)
ADD, SUB, MUL, DIV (Operazioni aritmetiche)
JMP (Jump)
CAL (Call di un blocco funzionale)
RET (Return da un blocco funzionale)
N (si trova dopo un operatore, nega il risultato)
•POU
Variabili
Funzioni
Blocchi Funzionali
Programmi
•T/R/C
Task: regola l'esecuzione di un programma a base ciclica periodica o una tantum
Risorsa: entità in grado di eseguire un programma (esempio, PLC)
Configurazione: elemento del linguaggio corrispondente ad un dispositivo
corrispondente a una o più risorse
•FUNZIONE (definizione testuale)
FUNCTION Nomefunzione : tipofunzione
VAR_INPUT Definizione variabili in ingresso
END_VAR
Corpo della funzione, eventuali valori di default alla funzione
END_FUNCTION
Può essere scritta in qualunque linguaggio eccetto SFC
•FUNZIONE (definizione grafica)
•Costrutti di controllo per funzioni definite graficamente
EN in ingresso per attivare il blocco
ENO in uscita quando la funzione è stata eseguita correttamente
•Blocco funzionale
Come la funzione, ma dipende anche da variabili interne e definibile anche in SFC
FUNCTION_BLOCK Nomeblocco
VAR_INPUT Definizione variabili in ingresso
END_VAR
VAR_OUTPUT Definizione variabili in uscita
END_VAR
Corpo della funzione, eventuali valori di default alla funzione
END_FUNCTION_BLOCK
•Flip Flop SR
•Flip Flop RS
•Contatore a incremento
•Contatore a decremento e bidirezionale
• CU = ingresso sui cui fronti di salita il contatore è incrementato
• CD = ingresso sui cui fronti di salita il contatore è decrementato
• R = reset (porta a zero il conteggio)
• PV = valore del conteggio di ingresso
• LD = carica il contatore con il valore PV
• Q = segnala che il contatore ha finito il conteggio (ha raggiunto
il valore del conteggio per il CTU oppure zero per il CTD)
• QD = segnala che il contatore CTUD ha raggiunto lo zero
• QU = segnala che il contatore CTUD ha raggiunto il valore PV
• CV = valore raggiunto dal contatore
Il limite di conteggio si supera mettendone in cascata
•Timer Pulse
•Timer On Delay
•Timer Off Delay
•Chiamata ad un blocco funzionale
•Programma
Sono delle specie di superblocchi funzionali, ma
- Posso definire le variabili direttamente in memoria
- Posso accedere direttamente agli input-output fisici del sistema
- Non possono istanziare sé stessi e vengono dichiarati a livello di risorsa
PROGRAM Nome
VAR_INPUT Definizione variabili in ingresso
END_VAR
VAR_OUTPUT Definizione variabili in uscita
END_VAR
Corpo della funzione, eventuali valori di default alla funzione
END_PROGRAM
•Assegnazione di una variabile ad un blocco di memoria (esterno)
Nomevariabile :=%X.1 (esempio di locazione di memoria)
•Task
Decidono l'esecuzione del programma
BOOL = esegui quando sale la variabile
INTERVAL DI TIPO TIME = esegui ogni time
NESSUNA VARIABILE = ciclico continuo
PRIORITA' = decide l'ordine di esecuzione. Se non settata è nulla. Decide il PLC se
un task può interromperne un altro
TASK Nome (SINGLE := Flag, o INTERVAL :=20ms, PRIORITY = 4);
Si associa ad un programma con WITH
Un programma non associato ad un task viene eseguito ciclicamente a priorità
minima
•Risorsa
RESOURCE Nome ON Processore
e poi si definiscono eventuali variabili globali
•Configurazione
Corrisponde alla definizione di tutto il software che va caricato su un PLC
• Lo scopo della configurazione è:
– definire le risorse a disposizione e allocare su di esse i programmi
– indicare la priorità di esecuzione dei programmi
– definire le variabili globali accessibili da tutti i programmi
CONFIGURATION
Definizione variabili globali
Definizione risorse
Definizione programmi e Task
END_CONFIGURATION
•Blocco Azione nell'SFC (qualificatori)
N = Non memorizzata, da eseguire fintanto che la fase è attiva, ed una volta quando
è disattivata
P = Una sola volta quando è attivata
D + Time = Ritardata di time quando la fase è ancora attiva, fino alla fine
dell'attivazione, ed una volta quando è disattivata
L + Time = Per il tempo Time + ancora una volta alla disattivazione
S+R = Set-Reset di un'azione memorizzata. Resta in esecuzione o meno
DS + Time = Azione ritardata e poi memorizzata se dopo il delay Time la fase è
ancora attiva
SL + Time = Azione Memorizzata e poi eseguita per il tempo X
•Blocco Azione nell'SFC (definizione grafica)
•Definizione testuale di connessione azione-fase
STEP nome_fase:
var_booleana(N); (* azioni senza *)
altra_var_booleana(P); (* corpo *)
AZIONE_COMPLESSA(L,t#30s,ind); (*a parte*)
END_STEP
•Fase:
Abilitata = Tutte le fasi a monte di essa sono attive
Superabile = Tutte le fasi a monte di essa sono attive e condizione associata è vera
Una fase superabile viene anche superata
•Traduzione tramite equazioni booleane
Un SFC può essere tradotto in equazioni booleane facendo un'equazione per ogni
fase: una di attivazione ed una di disattivazione (quindi attivazione non
superabilità).
Attivazione: La fase ha senso se alta la variabile delle transizioni a monte e quella
delle condizioni di uscita delle relative
Disattivazione: La fase ha senso se bassa la variabile della fase e (and, quindi
prodotto) not (condizioni di uscita alte and eventuali fini di altre fasi
sicnronizzate)
L'equazione poi finale sarà un “or” delle equazioni di attivazione e
disattivazione. Poi servono le equazioni delle azioni da eseguire
TROPPO LUNGO E COMPLESSO
•Traduzione SFC-LADDER (fasi)
Inizializzazione (setta ad uno le bobine delle fasi iniziali e poi jumpa ad azioni)
Valutazione delle transizioni (bobina fase + bobina condizione genera la bobina
transizione)
Aggiornamento della condizione (bobina fase setta le transizioni successive e
resetta le transizioni precedenti)
Esecuzione delle azioni (una fase fa scattare un'azione (possono esserci tanti or di
bobine)
•Traduzione SFC-LADDER (variabili temporali)
Le azioni che nell'SFC sono ritardate, si fanno introducendo dei blocchi funzionali
TIMER ON DELAY
Esercizio 1
Esercizio 2
Esercizio 3