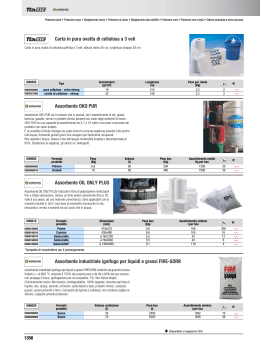
Luce dagli atomi
La nascita della spettroscopia e gli
albori della rivoluzione quantistica
8 h 3
u ( , T ) 
c3
1
h
e kT
1
Isaac Newton
(1642-1727)
1704
Oltre i limiti dello
spettro visibile
IR: 1800 (Herschel)
UV: 1801 (Ritter)
Frederick William Herschel
(1738-1822)
Ultravioletto: effetti fotochimici
Infrarosso: effetti termici
Jean Augustine Fresnel (1788 -1827)
Joseph von Fraunhofer (1787-1826)
Spettro ad alta risoluzione della radiazione solare
Gustav Robert Kirchhoff
(1824-1887)
Robert Wilhelm Eberhard von Bunsen
(1811-1899)
“Chemical Analysis by Observation of Spectra” -Annalen der Physik und der Chemie
(Poggendorff), Vol. 110 (1860), pp. 161-189 (dated Heidelberg, 1860)
Cesio (1860)
Rubidio (1861)
Saggi alla fiamma
Litio
Sodio
Potassio
Cesio
Calcio
Stronzio
Bario
Rame
7
3
Li
6.94
23
11
Na
22.99
39
19
K
39.10
85
37
Rb
85.47
Cs
133
55
132.91
40
20
Ca
40.08
88
38
Sr
87.62
Ba
138
56
137.33
63
29
Cu
63.55
Leybold, Köln, 1941
Franz Schmidt&Haensch, Berlin S., 1902
Franz Schmidt & Haensch, Berlin, ca. 1916
e( , T )
Potere emissivo: energia emessa dall’unità di
area alla temperatura assoluta T in un
intervallo unitario di frequenze. [J/m2]
a( , T )
Potere assorbente: frazione dell’energia incidente
assorbita dall’unità di area alla temperatura
assoluta T in un intervallo unitario di frequenze.
0  a( , T )  1
a( , T )  0
Specchio perfetto
a( , T )  1
Corpo nero
Legge di Kirchhoff
e( , T )
  ( , T )
a( , T )
Il rapporto tra il potere emissivo ed il
potere assorbente e’ indipendente dalla
natura del corpo e risulta quindi una
funzione universale della frequenza e
della temperatura assoluta.
 ( , T )
è il potere emissivo di un
corpo nero
c
 ( , T )  u ( , T )
4
u ( , T )
densità di energia
[J/(m3 s-1)]
Corollario della legge di Kirchhoff: ogni corpo in
equilibrio termico assorbe ed emette radiazioni alla
stessa frequenza.
Origine delle righe di Fraunhofer nello spettro solare
Cavità assorbente (corpo nero)
Distribuzione
spettrale della
radiazione di cavità
Wilhelm Wien (1864 -1928)
Legge dello spostamento di Wien
maxT  c3
c3  2,897756 mK 
Joseph Stefan (1835 -1893)
Legge di Stefan-Boltzmann
Ludwig Boltzmann
(1844 -1906)
c
 (T ) 
4


0
ca 4
u ( , T )d 
T  T4
4
  5,6705110
8
 W 
 2 4
m K 
John William Strutt
(Lord Rayleigh)
James Jeans
( 1842 -1919)
(1877 -1946)
Formula di Rayleigh Jeans
8
u ( , T )  3 kT
c
2
Max Planck (1858 -1947)
E  nh
n  0,1,2...
Formula di Planck (1900)
8 h 3
u ( , T ) 
c3
1
h
e kT
u ( , T ) 
1
8 hc

5
1
hc
e kT
1