Anno scolastico 2001-02 Liceo Scientifico “G.B. Pertile” di Asiago Progetto “Il cielo come laboratorio”, organizzato dal Dipartimento di Astronomia dell’Università degli Studi di Padova Enrico Benso Marco Ciatto Valentina Polato Patrick Rebeschini Giulia Valente INTRODUZIONE AL PROGETTO Il progetto pilota di astrofisica si è sviluppato in quattro lezioni, ciascuna delle quali con scopi e finalità eterogenei. La prima lezione, tenutasi a Thiene, ha fornito un supporto teorico ed in parte anche pratico utile per il lavoro che si sarebbe dovuto svolgere ad Asiago. Gli obbiettivi dei successivi due incontri all’osservatorio astrofisico di Asiago erano di raccogliere dati da osservazioni dirette, per poi elaborarli al computer, ma le condizioni atmosferiche non hanno consentito di procedere in tal modo. L’attività che ci ha coinvolti maggiormente è stata quindi la ricerca in rete, grazie alla quale abbiamo raccolto dati, informazioni storiche e scientifiche che ci hanno portati alla stesura della nostra relazione. Il lavoro in toto è stato presentato alla Specola, l’osservatorio patavino, dove ciascun gruppo ha esposto pubblicamente il frutto delle proprie ricerche e del proprio lavoro. PAROLE CHIAVE gravitazione, Newton, Galileo, Keplero, moto gravi, cannone alta montagna, sistema solare, pianeti, precessione perielio Mercurio INDICE 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Le tre leggi della dinamica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Le tre leggi di Keplero . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . La legge della gravitazione universale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . La terza legge di Keplero partendo da Newton . . . . . . . . . . . . . . . . . . . . . . Equivalenza tra il moto dei gravi e il moto della Luna intorno alla Terra . Sviluppi ulteriori della gravitazione (il problema dei tre corpi) . . . . . . . . . Problemi e critiche alla gravitazione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Il Sistema Solare . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.1 Classificazione dei pianeti del Sistema Solare . . . . . . . . . . . . . . . . . . . . . . 9.2 Distanze dei pianeti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Esempio applicazione terza legge di Keplero . . . . . . . . .. . . . . . . . . . . . . . . . Bibliografia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Pag. 2 » 2 » 3 » 3 » 3 » 4 » 5 » 5 » 6 » 6 » 8 » 9 » 10 1 1. Introduzione La teoria della gravitazione universale nasce ufficialmente nel 1687, anno in cui viene dato alle stampe l’opera principale di Isaac Newton (1642 - 1727), i “Principi Matematici della Filosofia Naturale” (vd. copertina nell’immagine sottostante). Questo libro è il risultato di una disputa iniziata alcuni anni prima nell’ambito della Royal Society, una associazione culturale fondata da scienziati, tra l’astronomo Edmund Halley ed il fisico Robert Hooke. Il tema della disputa, proposta da un altro eminente personaggio, l’architetto Christopher Wren, stava nello scoprire e dimostrare la relazione tra la forza attrattiva del Sole verso un pianeta e la distanza pianeta-Sole. C’era la convinzione che la relazione fosse di proporzionalità inversa al quadrato della distanza. In altre parole, al raddoppiare della distanza la forza diminuisce di quattro volte; al triplicare la distanza la forza diminuisce di nove volte e via dicendo. In formule: Serie di ritratti di Isaac Newton (incisione del maggio 1778) F ? 1/r2 dove F è la forza attrattiva ed “r” la distanza tra il pianeta ed il Sole. Tuttavia, nonostante questa convinzione, né Halley né Hooke erano capaci di dimostrare che questo fosse il risultato giusto. Halley allora ricorse all’aiuto di Newton che a quell’epoca ricopriva la cattedra di professore di matematica all’università di Cambridge. Il colloquio con Newton risultò molto proficuo per Halley perché Newton confermò che la legge matematica aveva quell’espressione perché Newton stesso alcuni anni prima l’aveva dimostrato per proprio conto. Stimolato dal quesito posto da Halley, Newton decise di rendere pubblici i suoi studi sia sulla gravitazione che sulla meccanica in generale. Tre anni dopo il colloquio tra Newton ed Halley veniva pubblicato, appunto i “Principia”. Tale testo può essere considerato a tutti gli effetti il primo vero e proprio trattato di fisica della storia, dove tra l’altro vengono enunciate le tre leggi della dinamica e la legge della gravitazione universale. 2. Le tre leggi della dinamica Nell’ambito dei suoi studi Newton ovviamente non partì da zero. Il primo che si era interessato di gravitazione fu naturalmente Galileo Galilei (1564 - 1642) con i suoi studi sulla caduta dei gravi. Gli studi di Galileo lo portarono a scoprire un fatto sorprendente che contraddiceva la fisica aristotelica: tutti i corpi cadono sulla Terra con la stessa accelerazione e di conseguenza, partendo da medesime altezze essi arrivano al suolo con la stessa velocità e quindi in tempi uguali. Ovviamente se proviamo a fare l’esperimento con la piuma ed il sasso, è quest’ultimo ad arrivare per primo. Questo capita perché oltre alla forza di gravità sono presenti altri fattori quali l’attrito. Se l’esperimento viene compiuto in condizioni ideali, allora entrambi i corpi giungono a terra allo stesso tempo. La fisica aristotelica affermava che il corpo di massa maggiore aveva una velocità di caduta superiore a quello di massa minore. Galileo smentì facilmente tale ipotesi. Galileo intuì anche il principio di inerzia, enunciato da Newton nei Principia. Dallo studio dei testi di Galileo e di Cartesio Newton enunciò le tre leggi della meccanica, con cui si aprono i Principia: - 1ª legge o principio d’inerzia:Ogni corpo permane nel suo stato di quiete o di moto rettilineo uniforme a meno che non sia costretto a mutare tale stato da forze impresse. - 2ª legge: F = m • a, dove “F” è la forza impressa ad un corpo, “m” la sua massa ed “a” l’accelerazione impartita al corpo. - 3ª legge o principio di azione e reazione: Ad ogni azione ne corrisponde una uguale e contraria. 2 3. Le tre leggi di Keplero Il testo di Newton continua con tutta una serie di dimostrazioni di teoremi di geometria e di definizioni che lo stesso Newton utilizza per dimostrare la dipendenza della forza attrattiva dal quadrato della distanza tra i due corpi. Newton aveva dimostrato tale dipendenza in modo analitico ma era stato “costretto” ad inventarsi una sua matematica per tale dimostrazione. La matematica che inventa Newton ora noi la chiamiamo “calcolo differenziale” e si studia in genere nell’ultimo anno di scuola superiore. Tuttavia nei Principia Newton non può pretendere di dimostrare tale legge con la sua nuova matematica così che la dimostrazione è geometrica. Inoltre la sua dimostrazione implica anche che le tre leggi di Keplero siano corrette dal punto di vista della teoria della gravitazione universale. Si ricorda qui che l’astronomo tedesco Keplero studiando il problema relativo alla forma dell’orbita del pianeta Marte enuncia nella sua opera del 1619 Astronomia Nova inizialmente due delle sue tre leggi a cui seguirà qualche anno più tardi anche la terza: - 1ª legge: I pianeti si muovono lungo orbite ellittiche in cui il Sole occupa uno dei due fuochi. - 2ª legge: La velocità del pianeta lungo la propria orbita non è costante: è maggiore quando il pianeta si trova perielio e minore quando si trova all’afelio. La velocità dei pianeti è tale che il raggio vettore che unisce il pianeta al Sole descrive in tempi uguali aree uguali. - 3ª legge (per tutti i pianeti): Occorre specificare (2ª legge) che il perielio è la distanza minima tra il pianeta ed il Sole mentre l’afelio è la distanza massima, inoltre (3ª legge) “r” è il semiasse maggiore dell’orbita (in una ellisse si hanno due assi di simmetria), “T” è il periodo di rivoluzione del pianeta attorno al Sole mentre “k” è una costante. L’aspetto singolare di queste tre leggi è che Keplero aveva verificato la loro validità solo per Marte e la Terra, generalizzando poi il risultato anche agli altri pianeti, senza nessuna prova osservativa. Inoltre le tre leggi sono il risultato esclusivo delle osservazioni di Keplero e del suo maestro Tycho Brahe; sono cioè delle leggi empiriche che non hanno nessun fondamento fisico. 4. La legge della gravitazione universale Nella teoria newtoniana della gravitazione le tre leggi di Keplero sono la naturale conseguenza della dipendenza della forza dal quadrato della distanza. In altre parole: se la forza attrattiva dipende dall’inverso del quadrato della distanza allora la traiettoria del corpo non può che essere una ellisse e viceversa. Grazie a Newton le leggi di Keplero acquistano anche un fondamento fisico. Newton va oltre e dimostra che la forza di gravità oltre che dalla distanza tra i corpi dipende in modo diretto anche dalle masse dei corpi stessi. Si arriva così alla notissima legge delle gravitazione universale, reperibile in qualsiasi testo di fisica: dove F è la forza gravitazionale attrattiva tra due corpi, M ed m le masse dei corpi ed r la distanza tra loro. Nella formula compare anche G che è la costante di gravitazione universale, un numero piccolissimo: 5. La terza legge di Keplero partendo da Newton Qui di seguito sono enunciati i passaggi che, partendo dalla legge della gravitazione universale di Newton, portano alla terza legge di Keplero: 3 Uguagliamo la forza di gravità alla forza centripeta. Ipotizzando le orbite come circolari (in buona approssimazione), eguagliamo la velocità ricavata dai passaggi precedenti con la velocità tangenziale. Ecco la terza legge di Keplero 6. Equivalenza tra il moto dei gravi e il moto della Luna intorno alla Terra Nei Principia Newton utilizzando il lavoro di Galileo sulle traiettorie dei proiettili ipotizza un esperimento ideale con cui mostra che la legge di caduta dei corpi spiega anche il moto dei pianeti attorno al Sole. Tale esperimento va sotto il nome di “cannone da alta montagna”. Newton immagina di porre su una alta montagna un cannone che spara proiettili via via più veloci, cioè con velocità iniziali sempre maggiori. Dagli esperimenti di Galileo si era visto che tutto ciò aveva come conseguenza di aumentare la “gittata” ideale del cannone: il proiettile toccherà terra sempre più lontano dal cannone. Nell’esperimento mentale di Newton si può pensare che ad un certo punto la velocità con cui viene sparato il proiettile sia tale che questo non tocchi più terra e si ponga in orbita alla stessa quota della montagna compiendo un percorso circolare. In pratica il proiettile pur obbedendo alla legge di caduta dei gravi e quindi cadendo continuamente sulla Terra non la raggiungerà mai, a meno che non cambino le condizioni di partenza. Questo appena descritto è il metodo con cui vengono messi in orbita i satelliti artificiali. Uno shuttle fa la parte della montagna, portando in quota il satellite che viene poi “sparato” ed inizia il suo percorso. Anche la Luna si comporta allo stesso modo: sta cadendo continuamente sulla Terra. Se si annullasse la forza di gravità, la Luna seguirebbe una traiettoria 4 tangenziale alla sua orbita perdendosi nello spazio, se invece si annullasse la sua rivoluzione lei cadrebbe lungo la verticale, verso la Terra. Da questo esperimento ideale Newton giunse alla conclusione che il corpo lasciato cadere, il proiettile, e la Luna si comportano tutti allo stesso modo: cadono sulla Terra per effetto della gravità quindi una stessa causa (la gravità) spiega un fenomeno terrestre ed uno celeste. La fisica della Terra può essere usata per spiegare i moti dei corpi celesti, unificando in tal modo le due classi di fenomeni. In senso rigoroso questa non è una unificazione di forze della natura ma solo una unificazione di classi di fenomeni. Da tutto il lavoro di Newton la gravità risulta essere una “azione a distanza” cioè i corpi si attraggono pur senza venire in contatto fisico. Tutto ciò veniva preso come un dato di fatto senza che venisse spiegato. Verso la fine dell’800 la teoria dell’elettromagnetismo di Maxwell introdurrà il concetto di “campo di forza” che verrà esteso anche alla gravità. Così come i fenomeni elettromagnetici vengono spiegati tramite l’effetto di un “campo di forza” elettromagnetica anche la gravità viene vista come un campo di forza che agisce a distanza. Occorrerà attendere il lavoro di Einstein del 1915 sulla Relatività Generale per avere una nuova teoria della gravitazione che completerà quella di Newton sostituendo al concetto di campo di forza il concetto di “curvatura” dello spaziotempo. Ma questo argomento esula dal tema trattato. 7. Sviluppi ulteriori della gravitazione (il problema dei tre corpi) Newton ancora nei Principia va oltre alla legge di gravitazione così come è stata espressa poche righe sopra. Egli capisce che tale legge si può estendere ad un numero qualsiasi di corpi che si attraggono, complicando molto il problema del ricavare la traiettoria del corpo in questione. Newton inizia ad analizzare il problema dei “tre corpi” nella fattispecie Terra-Sole-Luna. Scopre così che descrivere l’orbita della Luna attorno alla Terra, tenendo conto dell’influenza gravitazionale del Sole è un problema che va oltre alla matematica che lui stesso aveva inventato. Solo verso la fine del ‘700 i grandi matematici francesi, primo fra tutti Lagrange svilupperanno quella che ora viene chiamata “meccanica celeste” cioè lo studio delle perturbazioni che i vari pianeti del sistema solare generano a vicenda modificando e complicando notevolmente i calcoli delle orbite al punto che le soluzioni possono essere solo approssimate e mai esatte. Tuttavia proprio in virtù delle perturbazioni gravitazionali dei pianeti, nel 1846 viene scoperta una di queste perturbazioni nell’orbita del pianeta Urano. La perturbazione corrisponde ad un corpo e ne viene calcolata la sua orbita, si puntano i telescopi e viene scoperto il pianeta Nettuno. Tale scoperta rappresenta il trionfo completo della teoria della gravitazione di Newton. A buon diritto si verifica come le leggi della fisica valgono sia sulla Terra che nel cielo. 8. Problemi e critiche alla gravitazione La teoria di Newton estesa ai problemi di più corpi riesce a rendere conto di tutte le varie anomalie del moto dei pianeti tranne una: la precessione del perielio di Mercurio. In altre parole l’orbita di Mercurio non si chiude esattamente al punto di partenza ma ad ogni rivoluzione si sposta leggermente verso la direzione da cui arriva, cioè “precede” il punto di chiusura dell’orbita. Anche la Luna subisce questo effetto solo che per la Luna tale precessione è giustificata dalle perturbazioni del Sole ed altre note, mentre nessun effetto perturbativo su Mercurio giustifica il valore trovato: 43" ogni secolo. Un angolo piuttosto piccolo, ma pur sempre un neo nella teoria di Newton. Anche per spiegare questo effetto occorrerà attendere la teoria della Relatività Generale di Einstein. All’epoca della pubblicazione dei Principia i detrattori di Newton lo accusavano di avere introdotto, con la gravità, delle forze occulte perché lui non spiega cosa sia la gravità. Newton si limita solo a fornire una espressione matematica che funziona e che fino all’inizio del nostro secolo avrà una totale validità. Occorre però sottolineare che nessun altro sarà capace di spiegare in termini qualitativi cosa sia la gravità. Solo Einstein ne sarà capace e per molti decenni tale spiegazione sarà un qualcosa di troppo complicato per i fisici suoi contemporanei. 5 9. Il Sistema Solare Il Sistema Solare è un insieme di corpi celesti in rotazione attorno al Sole. Ne fanno parte, oltre al Sole stesso, 9 pianeti, 61 satelliti, alcune migliaia di asteroidi, ed un numero imprecisato di comete. Partendo dal Sole, troviamo per primi i pianeti interni, Mercurio e Venere, poi la Terra e infine i pianeti esterni: Marte, Giove, Saturno, Urano, Nettuno e Plutone. Tra l'orbita di Marte e quella di Giove c'è la fascia degli asteroidi. Dal punto di vista dinamico, il Sistema Solare è un insieme molto complesso e particolare. Tutti i pianeti ruotano nello stesso verso, cioè in senso antiorario rispetto ad un ipotetico osservatore posto sul polo nord del Sole. Le loro orbite giacciono quasi tutte sullo stesso piano, cioè sono inclinate al massimo di 2,5 gradi rispetto al piano dell'eclittica, ad eccezione di quelle di Mercurio (7 gradi) e di Plutone (17 gradi). Le orbite sono pressochè circolari, tranne quelle di Plutone (che ha un'eccentricità pari a 0.25) e di Mercurio (0.20). Le orbite dei pianeti interni L'estensione totale del Sistema Solare è di circa 6 miliardi di Km, pari a 39,3 U.A.. I corpi del Sistema Solare occupano in realtà un volume molto piccolo rispetto alle dimensioni complessive. Il Sistema Solare è quindi praticamente "vuoto": se il Sole fosse una sfera del diametro di un metro, la Terra avrebbe le dimensioni di un pisello e sarebbe posta a 108 metri di distanza da esso, Giove avrebbe le dimensioni di un'arancia, posta a 550 metri, ed infine Plutone disterebbe 4 km e misurerebbe meno di un millimetri di diametro. Le orbite dei pianeti esterni 9.1 Classificazione dei pianeti del Sistema Solare Le caratteristiche che distinguono i vari pianeti sono quelle fisiche e quelle relative al loro moto di rivoluzione attorno al Sole e di rotazione attorno al proprio asse. Le caratteristiche fisiche sono: dimensioni, massa, densità media; intensità di un eventuale campo magnetico; composizione chimica; presenza e composizione dell'atmosfera. Quelle relative al moto sono: le dimensioni dell'orbita, l'eccentricità, l'inclinazione del piano orbitale e Il Sole e i pianeti, dell'asse di rotazione rispetto al piano dell'eclittica, il periodo approssimativamente nella scala di orbitale e il periodo di rotazione. dimensioni reale Infine, i vari pianeti si distinguono per l'eventuale presenza ed il numero di satelliti. Sotto entrambi gli aspetti, i pianeti del nostro Sole sembrano formare due sistemi distinti: una sorta di sistema solare interno, composto dai PIANETI TELLURICI o ROCCIOSI (Mercurio, Venere, la Terra e Marte) e uno esterno, che comprende i PIANETI GIGANTI (Giove, Saturno, Urano e Nettuno). Plutone 6 sembra per molti versi un pianeta anomalo, che non fa parte di nessuno dei due sottosistemi. PIANETI ROCCIOSI O TELLURICI: I pianeti terrestri. Le dimensioni sono in scala I pianeti rocciosi hanno dimensioni relativamente modeste (meno di 15.000 Km di diametro) e densità abbastanza alte (da 3 a 5, dove 1 è la densità dell'acqua). Essi sono composti di un nucleo ferroso circondato da un mantello basaltico. Rispetto ai pianeti giganti, il loro moto di rivoluzione è più veloce e la loro rotazione è più lenta. I pianeti rocciosi sono piuttosto diversi tra loro per quanto riguarda l'atmosfera (quando presente), la superficie del suolo, il campo magnetico e i parametri orbitali, in contrasto con la relativa uniformità dei pianeti giganti. PIANETI GIGANTI: I pianeti gioviani. Le dimensioni sono in scala I pianeti giganti devono il loro nome alle notevoli dimensioni (hanno diametri maggiori di 50.000 Km). Essi hanno densità prossime ad 1 e si dividono a loro volta in pianeti gassosi (Giove e Saturno) e pianeti di ghiaccio (Urano e Nettuno). I pianeti gassosi sono composti da un nucleo roccioso circondato da un mantello liquido, a sua volta ricoperto da uno spesso strato di gas. I pianeti di ghiaccio sono composti invece da un nucleo di roccia, ricoperto da uno strato di ghiaccio, il tutto circondato da un'atmosfera. I periodi di rivoluzione dei pianeti giganti sono molto più lunghi rispetto a quelli dei pianeti tellurici, e vano da circa 12 anni (Giove) a quasi 165 (Nettuno). Viceversa essi ruotano più rapidamente dei pianeti rocciosi: ne deriva una notevole forza centrifuga all'equatore, e quindi una forma più schiacciata. Giove, Saturno e Urano possiedono inoltre un insieme di anelli composti da polvere e frammenti di roccia e ghiaccio di varie dimensioni. Infine, tutti i pianeti giganti possiedono un gran numero di satelliti, mentre quelli rocciosi ne hanno al massimo due. Giove e Saturno hanno la particolarità di emettere 2 volte e mezzo più energia di quanta non ne ricevano dal Sole. Questa energia deriva loro da una lenta contrazione gravitazionale, che riscalda il loro nucleo. Inoltre nella loro atmosfera il rapporto idrogeno-elio è molto simile a quello solare; questo fa pensare che i due pianeti siano in realtà due "stelle mancate": se fossero più massicci, la pressione e la temperatura del gas al loro interno sarebbero sufficienti ad innescare le reazioni termonucleari e a farli diventare stelle. PLUTONE Plutone e il suo satellite Caronte Plutone è il meno conosciuto di tutti i pianeti. Esso sembra un caso a parte rispetto agli altri, sia per la sua orbita anomala, sia per tipo e dimensioni. Esso infatti, pur essendo situato nella regione dei pianeti giganti, è molto piccolo e di tipo roccioso. Si pensa che Plutone possa essere un ex satellite di Nettuno, sfuggito alla sua attrazione gravitazionale per sistemarsi su un'orbita indipendente attorno al Sole. 7 9.2 Distanze dei pianeti Le distanze dei pianeti rispetto al Sole seguono la legge di Titius-Bode, che è stata determinata empiricamente nel 1772. In base ad essa, le distanze dei vari pianeti dal Sole si ottengono moltiplicando la distanza del precedente per un coefficiente pari a 1,75. Se prendiamo come unità di misura la distanza Terra-Sole, gli altri pianeti avranno distanze rispettivamente pari a: PIANETA TEORIA (Titius-Bode) Mercurio Venere Marte Asteroidi Giove Saturno Urano Nettuno Plutone 0.4 0.7 1.6 2.8 5.2 10.0 19.6 38.8 77.2 DISTANZA REALE 0.387 0.723 1.524 2.767 5.203 9.539 19.189 30.060 39.439 Anche la fascia degli asteroidi segue questa legge, occupando il posto compreso tra Marte e Giove. Nettuno e Plutone costituiscono invece delle eccezioni, in quanto la loro distanza ha un grosso scarto rispetto a quella prevista. Questo confermerebbe una volta di più la natura anomala di Plutone. Corpi minori Oltre ai pianeti ci sono una miriade di corpi minori nel Sistema Solare, essenzialmente suddivisi in tre classi. Gli asteroidi sono piccoli oggetti rocciosi delle dimensioni comprese tra pochi cm e 1.000 Km. Essi orbitano a migliaia in una fascia compresa tra le orbite di Marte e di Giove. Le comete sono corpi celesti che ruotano a grande distanza dal Sole, lungo orbite molto eccentriche. Esse sono sostanzialmente costituite da un aggregato di roccia e ghiaccio di dimensioni minori di 10 Km. Il loro aspetto caratteristico è dovuto al fatto che, quando passano vicino al Sole, la superficie del loro nucleo di ghiaccio vaporizza a causa dell'elevata temperatura. Il gas che si produce forma cosi' un alone diffuso, quasi sferico, detto chioma. La radiazione del Sole e il vento solare esercitano su questo gas una pressione. Essa deforma la chioma spingendo il gas in direzione opposta al Sole e dando origine alla caratteristica coda, una striscia di gas lunga decine o anche centinaia di milioni di chilometri. La cometa West Le meteoriti sono i resti di corpi solidi, metallici o pietrosi, penetrati nell'atmosfera terrestre ad alte velocità. L'attrito con l'atmosfera fa si' che essi si riscaldino e si disgreghino: i più piccoli vengono ridotti in polvere, mentre i più grandi non vengono distrutti completamente e possono raggiungere il suolo. Una metorite condritica ritrovata in Antartide 8 10. Esempio applicazione terza legge di Keplero (Calcolo della massa del Sole attraverso la terza legge di Keplero) r = distanza media dal sole T = periodo di rivoluzione Ms = massa del Sole Sostituiamo i valori di “r” e “T” di tutti i pianeti del sistema solare nella seguente formula (ricavata dalla terza legge di Keplero): Ottenendo in tal modo i seguenti valori di “Ms”: ? ? Mercurio: r = 57.6 • 109 m T = 88 • 86400 s Ms = 1.95556 • 1030 Kg ? ? Venere: r = 108.2 • 109 m T = 224.7 • 86400 s Ms = 1.98832 • 1030 Kg ? ? Terra: r = 149.6 • 109 m T = 365.26 • 86400 s Ms = 1.9888 • 1030 Kg ? ? Marte: r = 227.9 • 109 m T = 687 • 86400 s Ms = 1.9876 • 1030 Kg ? ? Giove: r = 760.3 • 109 m T = 11.86 • 86400 • 365.26 s Ms = 1.99102 • 1030 Kg ? ? Saturno: r = 1427 • 109 m T = 29.46 • 86400 • 365.26 s Ms = 1.9889 • 1030 Kg ? ? Urano: r = 2870.1 • 109 m T = 84.01 • 86400 • 365.26 s Ms = 1.9899 • 1030 Kg ? ? Nettuno: r = 4498.6 • 109 m T = 164.8 • 86400 •365.26 s Ms = 1.991 • 1030 Kg ? ? Plutone: r = 5900 • 109 m T = 247.7 • 86400 • 365.26 s Ms = 1.9884 • 1030 Kg In buona approssimazione questi valori di “Ms” si avvicinano al valore reale della massa del sole: Ms = 1.99 •1030 Kg 9 11. Bibliografia TESTI Fisica 1 – Fondamenti di meccanica, M.E. Bergamaschini, P. Marazzini, L. Mazzoni, Carlo Signorelli Editore, 1996, Milano. SITI INTERNET http://ipertesi.url.it/freew/fisica1.htm http://www.brera.unimi.it/Atti-Como-99/Banfi.pdf http://www.lorenzoroi.net/astro/CorsoAstro2.pdf http://www.racine.ra.it/planet/testi/uniforze.htm http://www.racine.ra.it/planet/testi/newton.htm http://www.phy.ntnu.edu.tw/java/Kepler/Kepler.html 10
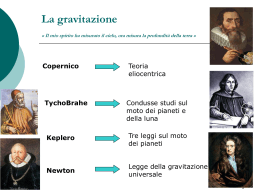
Scaricare