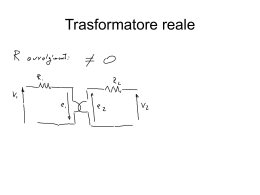
INDUTTORI BIPORTA
Il funzionamento degli induttori biporta fa riferimento alla modellizzazione dei fenomeni di
accoppiamento magnetico tra due circuiti che sono fisicamente separati. Il flusso magnetico
prodotto da uno dei due circuiti mediante variazioni temporali di corrente nel circuito stesso,
induce, secondo la legge di Faraday, una tensione nell’altro circuito. Tale induzione di tensione fa
riferimento al flusso magnetico comune alle due bobine avvolte su un supporto magnetico o anche
disposte in aria. Per fissare le idee si consideri un particolare esempio attraverso il quale sarà
possibile identificare i legami funzionali tra le due coppie di correnti e flussi delle due bobine.
Si consideri un toroide intorno a cui sia disposto un avvolgimento costituito da N1 spire di materiale
conduttore, come mostrato in figura:
Si riterranno, inoltre, soddisfatte le seguenti ipotesi di lavoro:
• il toroide deve avere una sezione retta S costante e circolare;
• il toroide è costituito da materiale con permeabilità magnetica µ costante con μ μ0 ;
• le spire dell’avvolgimento sono disposte in modo serrato tra loro lungo tutto lo sviluppo del
toroide e a simmetria radiale;
• il toroide deve avere una struttura filiforme, ossia deve essere soddisfatta la condizione:
d 2 − d1 d1 .
Queste ipotesi garantiscono che:
• le linee di flusso del campo magnetico generato dalla corrente che viene fatta scorrere
nell’avvolgimento siano contenute all’interno del toroide;
• il campo magnetico è diretto tangenzialmente ad ogni circonferenza con centro in O e con
diametro compreso tra d1 e d2 (il verso del vettore campo magnetico dipenderà dal verso di
scorrimento della corrente e può essere determinato con la regola della mano destra);
• il campo magnetico è costante in modulo lungo tutto il toroide.
Si consideri, allora, un cammino medio C (come mostrato in figura) di diametro: d =
e si applichi il teorema di Ampere a tale cammino chiuso, si ottiene:
v∫ H1 ⋅ d l = N1i1 ⇔ H1π d = N1i1 ⇒ H1 =
C
d1 + d2
2
N1i1
πd
ove H1 rappresenta il campo magnetico dovuto ad i1 mentre N1i1 rappresenta il numero di
concatenamenti di i1 con C.
1
Noto il valore del campo magnetico si può ottenere il campo di induzione magnetica come segue:
B1 = μ H1 =
μ N1
i
πd 1
e quindi l'espressione del flusso del campo magnetico generato dalla corrente i1 e concatenato ad
una generica spira dell’avvolgimento di sezione S. Tale flusso, nella generica sezione S del toro,
varrà:
ϕ 1 = ∫ B1 ⋅ ds = B 1 S =
S
μS
N 1i 1
πd
che si può scrivere come:
ϕ12 = Λ12 N1i1 dove in generale si ha Λ =
1 μS
=
ℜ πd
dove Λ è detta permeanza mentre ℜ è detta riluttanza magnetica.
Queste grandezze in generale dipendono dal mezzo che è attraversato dalle linee del flusso
magnetico e dal percorso effettuato. Per cui se si suppone che ci siano anche delle linee di flusso
generate dalla corrente i1 e che si chiudono concatenandosi con le spire della prima bobina
attraverso un cammino che non passa per il toroide considerato si ha un secondo contributo al flusso
totale di una generica spira dell’avvolgimento di sezione S, esso è dato da:
ϕ11 = Λ11 N1i1
dove la differenza rispetto al caso precedente è data dal fatto che il cammino sul quale si calcola il
campo H è diverso dal caso precedente (si ha quindi una diversità di percorso ed una conseguente
variazione anche della permeabilità magnetica µ in funzione del percorso stesso), è chiaro che in
questo caso si stanno rilasciando le ipotesi iniziali secondo le quali si supponeva che le linee di
flusso del campo magnetico generato dalla corrente i1 siano contenute all’interno del toroide. In
altre parole, il considerare anche il secondo contributo risponde alla supposizione di considerare un
flusso disperso per il campo magnetico.
Se si pone ora un secondo avvolgimento sul toroide come mostrato nella figura in basso, dove per
chiarezza di disegno il secondo avvolgimento è disegnato separato dal primo, ma che in realtà è da
considerarsi sovrapposto al primo. In maniera analoga a quanto fatto per il primo avvolgimento, si
può ottenere il flusso del campo magnetico generato dalla corrente i2 attraverso una generica
sezione S del toroide, esso è pari a:
ϕ21 = Λ 21 N 2i 2
(Nota: tale flusso viene calcolato considerando unicamente il secondo avvolgimento).
ed un flusso:
ϕ22 = Λ 22 N 2i 2
che non segue il cammino lungo il toroide, ma che si chiude sul secondo avvolgimento senza
passare per il primo. In definitiva si ha:
2
ϕ11 = Λ11 N1i1 flusso dovuto a i1 che interessa solo il primo avvolgimento;
ϕ12 = Λ12 N1i1 flusso dovuto a i1 che interessa il primo ed il secondo avvolgimento;
ϕ21 = Λ 21 N 2i 2 flusso dovuto a i2 che interessa il primo ed il secondo avvolgimento;
ϕ22 = Λ 22 N 2i 2 flusso dovuto a i2 che interessa solo il secondo avvolgimento.
Nella figura riportata in alto sono indicati per meglio identificare la situazione in esame i precorsi
dei flussi ϕ11 e ϕ12 con le linee tratteggiate.
A questo punto si supponga di far passare una corrente i1 diversa da zero nel primo avvolgimento e
di mantenere il secondo avvolgimento in condizione di circuito aperto; si può così ricavare il flusso
del campo magnetico generato dalla corrente i1 e concatenato, rispettivamente, al primo e al
secondo avvolgimento come segue:
2
2
⎧i1 ≠ 0 ⎧⎪Φ11 = N1 (ϕ11 + ϕ12 ) = Λ11 N1 i1 + Λ12 N1 i1
⇒⎨
⎨
⎩i 2 = 0 ⎩⎪Φ12 = N 2ϕ12 = Λ12 N1 N 2i1
Allo stesso modo si supponga di far passare una corrente i2 diversa da zero nel secondo
avvolgimento e di mantenere il primo avvolgimento in condizione di circuito aperto; si può così
ricavare il flusso del campo magnetico generato dalla corrente i2 e concatenato, rispettivamente, al
primo e al secondo avvolgimento come segue:
⎧⎪Φ 21 = N1ϕ 21 = Λ 21 N1 N 2i 2
⎧i1 = 0
⇒⎨
⎨
2
2
⎩i 2 ≠ 0 ⎩⎪Φ 22 = N 2 (ϕ 22 + ϕ 21 ) = Λ 22 N 2i 2 + Λ 21 N 2i 2
Se si considera, quindi, la situazione nella quale si fa passare una corrente i1 diversa da zero nel
primo avvolgimento ed una corrente i2 diversa da zero nel secondo avvolgimento, il flusso del
campo magnetico generato dalla corrente i1 e dalla corrente i2 concatenato, rispettivamente, al
primo e al secondo avvolgimento si ottiene, applicando il principio di sovrapposizione, infatti, il
sistema in esame è lineare, come segue:
(
)
2
2
2
2
⎧
⎧i1 ≠ 0
⎪Φ1 = Φ11 + Φ12 = Λ11 N1 i1 + Λ12 N1 i1 + Λ 21 N1 N 2i 2 = Λ11 N1 + Λ12 N1 i1 + Λ 21 N1 N 2i 2
⇒⎨
⇒
⎨
⎩i 2 ≠ 0 ⎪⎩Φ 2 = Φ 21 + Φ 22 = Λ12 N1 N 2i1 + Λ 22 N 22i 2 + Λ 21 N 22i 2 = Λ12 N1 N 2i1 + Λ 22 N 22 + Λ 21 N 22 i 2
⎧Φ1 = L1i1 + Mi 2
⎨
⎩Φ 2 = Mi1 + L 2i 2
(
)
avendo posto:
3
L1 = N12 ( Λ11 + Λ12 )
M = Λ 21 N1 N 2 = Λ12 N1 N 2
L2 = N 22 ( Λ 22 + Λ 21 )
infatti, normalmente si ha: Λ 21 = Λ12 .
il sistema sopra si può scrivere come:
⎡ Φ ⎤ L M ⎤ ⎡ i1 ⎤
⎧Φ1 = L1i1 + Mi 2
o in forma matriciale: Φ = ⎢ 1 ⎥ = ⎡⎢ 1
⎨
⎥ ⋅ ⎢ ⎥ = L ⋅i
⎩Φ 2 = Mi1 + L 2i 2
⎣Φ 2 ⎦ ⎣M L2 ⎦ ⎣i 2 ⎦
dove la matrice L è detta matrice induttanza.
Nota: Come si può osservare, queste equazioni rappresentano la caratteristica di un induttore
biporta; infatti la rappresentazione è del tipo:
⎧fa (i 1 , i 2 ,ϕ 1 ,ϕ 2 ) = 0
⎨
⎩fb (i 1 , i 2 ,ϕ 1 ,ϕ 2 ) = 0
dove ciascuna delle funzioni fa e fb rappresentano un elemento definito nello spazio a 4 dimensioni
che a due a due sono correnti e flussi (i, φ).
La rappresentazione circuitale di un induttore biporta è la seguente:
La caratteristica sopra può essere facilmente espressa in termini di tensioni e correnti, infatti dalla
precedente si ricavano facilmente le relazioni tra tensioni e correnti di porta:
dΦ1
di1
di 2
⎧
⎪⎪ v1 = dt = L1 dt + M dt
⎨
⎪ v = dΦ 2 = M di1 + L di 2
2
⎪⎩ 2
dt
dt
dt
mediante le quali si può ottenere la seguente interpretazione circuitale equivalente di un induttore
biporta:
4
Oppure, supponendo che i due induttori accoppiati siano inizialmente scarichi (cioè con corrente
iniziale nulla), si può scrivere:
⎡ i1 ⎤
⎡ L2
1
⎢i ⎥ = det( L) ⋅ ⎢ − M
⎣ 2⎦
⎣
⎡t
⎤
v1 (τ ) dτ ⎥
⎢
∫
−M ⎤ ⎢ 0
⎥ = ⎡ Γ1
⋅ t
⎥
⎥ ⎢⎣ Γ 0
L1 ⎦ ⎢
⎢ ∫ v2 (τ )dτ ⎥
⎣0
⎦
⎡t
⎤
v1 (τ )dτ ⎥
⎢
∫
Γ0 ⎤ ⎢ 0
⎥
⋅
⎥
Γ 2 ⎥⎦ ⎢ t
⎢ ∫ v2 (τ )dτ ⎥
⎣0
⎦
dove si è posto:
⎡Γ
Γ = L−1 = ⎢ 1
⎣Γ0
Γ0 ⎤
L2
L1
M
Γ2 =
Γ0 = −
, con Γ1 =
⎥
Γ2 ⎦
det(L)
det(L)
det(L)
ove Γ indica la matrice delle inertanze.
Se si usa quest’ultima versione per le relazioni della caratteristica di due induttori accoppiati si
ottiene, invece, la seguente ulteriore interpretazione circuitale equivalente di un induttore biporta:
Questo elemento viene utilizzato spesso in circuiti in regime sinusoidale, per ottenere la relazione
caratteristica di questo elemento in regime sinusoidale si deve passare all’utilizzo dei fasori per le
variabili tensione e corrente. Si ha facilmente:
⎧⎪V1 = jω L1 I1 + jω MI 2
⎨
⎪⎩V2 = jω MI1 + jω L 2 I 2
che può anche essere messa in forma matriciale come la corrispondente relazione nel tempo.
⎡V1 ⎤
⎡ L1 M ⎤ ⎡ I1 ⎤
⎢ ⎥ = jω ⎢
⎥⎢ ⎥
⎣ M L2 ⎦ ⎣ I 2 ⎦
⎣V2 ⎦
5
Infine un’ultima osservazione. Dalle equazioni:
L1 = N12 ( Λ11 + Λ12 )
M = Λ 21 N1 N 2 = Λ12 N1 N 2
L2 = N 22 ( Λ 22 + Λ 21 )
si deduce che M 2 = Λ 2 N 2 N 2 ≤ L1 L2 = N12 N 22 ( Λ11 + Λ12 )( Λ 22 + Λ 21 )
allora si definisce coefficiente di accoppiamento la quantità:
21
k=
M
1
2
⇒ M =k L11L 22 con 0 ≤ k ≤ 1
L11L 22
che costituisce una misura dell’accoppiamento magnetico tra le due bobine.
Se k=0 allora M=0 e l’elemento circuitale definito in precedenza si comporta come due induttori
separati senza reciproca interazione.
Se k=1 allora M 2 = L1 L2 per cui si ha: Λ12 = Λ 21 = 0 il che vuol dire che tutte le linee di flusso del
campo magnetico generato da una delle due bobine si concatenano con l’altra bobina.
Infine, il considerare per M il valore assoluto dipende dal fatto che questa quantità come si vedrà
nel seguito può avere valori sia positivi sia negativi. Prima di fare questo si consideri la
caratterizzazione energetica di un induttore biporta.
Caratterizzazione energetica di un induttore biporta.
Si considera, ora, l'induttore biporta da un punto di vista energetico. Si supponga che all'istante t=0
le correnti sui due induttori accoppiati siano nulle, cioè:
i 1 (0) = 0
i 2 (0) = 0
e
⎧Φ = L1i1 + Mi 2
Dalle relazioni ⎨ 1
che esprimono la caratteristica di un induttore biporta, si ottiene:
⎩Φ 2 = Mi1 + L 2i 2
Φ 1 (0) = 0
e
Φ 2 (0) = 0 .
Essendo nulli i flussi, si assume questa condizione come quella a cui corrisponde energia magnetica
immagazzinata dal biporta uguale a zero all’istante t=0.
Considerando questa condizione si ricava ora l’energia assorbita dall’induttore biporta in un
intervallo di tempo [0,t].
La potenza per un elemento biporta è data per definizione da:
p(t) = v1 (t)i1 (t) + v 2 (t)i 2 (t)
di ⎞
di ⎞
⎛ di
⎛ di
p(t) = i1 (t)v1 (t) + i 2 (t)v 2 (t) = i1 (t) ⎜ L1 1 + M 2 ⎟ + i 2 (t) ⎜ M 1 + L 2 2 ⎟
dt ⎠
dt ⎠
⎝ dt
⎝ dt
quindi
6
p(t) = i1 (t)v1 (t) + i 2 (t)v 2 (t) = L1i1 (t)
= L1i1 (t)
di1
di
di
di
+ Mi1 (t) 2 + Mi 2 (t) 1 + L 2i 2 (t) 2 =
dt
dt
dt
dt
di1
d
di
+ M ( i1 (t)i 2 (t) ) + L 2i 2 (t) 2 .
dt
dt
dt
per cui l’energia in un intervallo infinitesimo dt è ottenuta da:
t
t
di
di ⎞
d
⎛
w(0,t) = ∫ p(t)dt = ∫ ⎜ L1i1 (t) 1 + M ( i1 (t)i 2 (t) ) + L 2i 2 (t) 2 ⎟ dt
dt
dt
dt ⎠
0
0⎝
integrando quest’ultima relazione tra gli estremi 0 e t e ricordando l’ipotesi per cui l’energia
magnetica nell’istante 0 è nulla, si può scrivere:
1
⎛1
⎞
w(t) = ⎜ L1i12 + Mi1i 2 + L 2i 22 ⎟
2
⎝2
⎠
che è la relazione che esprime l’energia fornita all’induttore biporta nell’intervallo [0,t].
Se, invece, si considera il funzionamento degli induttori mutuamente accoppiati nel funzionamento
in regime sinusoidale si ha che la potenza complessa è data da:
1
1
1
1
1
N = V1 I 1∗ + V2 I 2∗ = jω L1 I1 I1∗ + jω MI 2 I1∗ + jω MI1 I 2∗ + jω L 2 I 2 I 2∗ =
2
2
2
2
2
1
1
1
1
= jω L1 I12 + jω MI 2 I1∗ + jω MI1 I 2∗ + jω L 2 I 22 =
2
2
2
2
1
1
1
= jω L1 I12 + jω M I 2 I1∗ + I1 I 2∗ + jω L 2 I 22 =
2
2
2
1
1
= jω L1 I12 + jω MI1 I 2 cos (α1 − α 2 ) + jω L 2 I 22
2
2
(
)
(
)
infatti I 2 I1∗ + I1 I 2∗ = ( I 2 I1∗ ) + I1 I 2∗ = 2 Re ⎡⎣ I1 I 2∗ ⎤⎦ = 2 I1 I 2 cos (α1 − α 2 )
∗
dove α1 e α 2 sono le fasi delle due correnti.
Da quanto sopra descritto si evince come la potenza complessa per questo elemento sia di fatto una
quantità puramente immaginaria, in altri termini la potenza attiva è nulla, quindi si deduce
immediatamente che per un induttore biporta tutta la potenza che entra dovrà essere prima o poi
ceduta senza essere dissipata. L’induttore biporta è quindi un elemento reattivo ed ai fini energetici
si comporta come un induttore o un condensatore, per cui è anche un elemento passivo.
%%%%%%%%%%%%%%%%
Un modo per valutare se l’energia di un induttore biporta è o meno positiva fa riferimento alla
seguente osservazione.
Osservazione:
Si osserva che questa energia è quella immagazzinata dallo stesso induttore biporta, è una quantità
maggiore o al massimo uguale a zero, perché non essendoci nell’induttore biporta altri morsetti
(escludendo, ovviamente, le coppie di terminali che definiscono le due porte) attraverso i quali esso
può scambiare energia con i sistemi interagenti in maniera reversibile, né generatori, si ha che tale
energia potrà, al limite, essere restituita completamente al resto del circuito collegato all’induttore
7
biporta (in tal caso: W(t)=0) ma quest’ultimo non potrà mai cedere all’esterno una quantità di
energia superiore a quella che riceve.
Di conseguenza, osservando che l’espressione sopra può essere posta in forma matriciale come
segue:
W=
⎡L M ⎤ ⎡ i ⎤ 1
1
[i1 i 2 ] ⋅ ⎢ M1 L ⎥ ⋅ ⎢i1 ⎥ = iT Li ≥ 0
2
2
2⎦ ⎣ 2⎦
⎣
se ne deduce che l'energia magnetica immagazzinata dall’induttore può essere considerata una
forma quadratica semidefinita positiva e quindi tutti i minori principali estratti della matrice L
risulteranno essere non negativi, ossia:
L1 ≥ 0
L2 ≥ 0
Det ( L ) = L1L 2 − M 2 ≥ 0 ⇒ M 2 ≤ L1L 2
Dall'ultima relazione, si osserva che la mutua induttanza M può assumere anche valori negativi e
quindi sorge il problema di determinare il segno di M. Prima di far ciò, è opportuno introdurre il
seguente parametro:
k=
M
L11L 22
⇒ M =k L11L 22 con 0 ≤ k ≤ 1
k è detto coefficiente di accoppiamento: se è uguale a zero i due induttori non sono accoppiati, se
è uguale a 1 l'accoppiamento è perfetto ed M assume il suo valore massimo.
%%%%%%%%%%%%%%%%%%%%%%%%%
Segno di M
Per quanto riguarda ora la determinazione del segno di M è possibile verificare che tale segno
dipende dal senso di avvolgimento delle spire intorno al materiale magnetico. Si consideriamo, ad
esempio, il toroide rappresentato nella figura in basso e si supponga, per comodità, che le correnti
nei due avvolgimenti siano costanti (si tenga presente che si fa riferimento alla convenzione degli
utilizzatori):
Come si può verificare applicando la regola della mano destra, il flusso del campo magnetico
generato dalla corrente del primo avvolgimento è diretto in senso orario e poiché anche il flusso del
campo magnetico generato dalla corrente nel secondo avvolgimento ha la stessa direzione, si può
8
concludere che quest’ultimo rafforza il primo. Se invece si inverte il verso della corrente sul
secondo avvolgimento, cioè si considera una corrente sempre entrante, ma pari a -I2, il flusso del
campo magnetico generato da tale corrente sarà diretto in senso antiorario e quindi si oppone al
flusso del campo magnetico generato dalla corrente nel primo avvolgimento. Si può allora ritenere
che l'energia magnetica nel primo caso sarà maggiore di quella nel secondo caso, cioè:
1
1
L 11 I12 + M I1 I 2 + L 22 I 22
2
2
1
1
2)W (I1 , − I 2 ) = L 11 I12 − M I1 I 2 + L 22 I 22
2
2
W (I1 ,I 2 ) > W (I1 , − I 2 ) ⇒ M I1 I 2 > − M I1 I 2
1)W (I1 ,I 2 ) =
Evidentemente, affinché quest’ultima relazione sia soddisfatta M deve essere positivo. Si immagini
ora di cambiare il senso del secondo avvolgimento, come mostrato in figura:
Come si può verificare applicando la regola della mano destra, il flusso del campo magnetico
generato dalla corrente del primo avvolgimento è diretto in senso orario mentre il flusso del campo
magnetico generato dalla corrente nel secondo avvolgimento è diretto in senso antiorario; si può,
quindi, concludere che quest’ultimo si oppone al primo. Se, invece, si inverte il verso della corrente
sul secondo avvolgimento, cioè si considera una corrente sempre entrante ma pari a -I2, il flusso del
campo magnetico generato da tale corrente sarà diretto in senso orario e perciò rafforza il flusso del
campo magnetico generato dalla corrente nel primo avvolgimento. Si può allora ritenere che
l'energia magnetica nel secondo caso sarà maggiore di quella nel primo caso, cioè:
1
1
L11I12 + MI1I 2 + L 22 I 22
2
2
1
1
2)W(I1 , − I 2 ) = L11I12 − MI1I 2 + L 22 I 22
2
2
W(I1 , − I 2 ) > W(I1 ,I 2 ) ⇒ -MI1I 2 > MI1I 2
1)W(I1 ,I 2 ) =
Evidentemente, affinché quest’ultima relazione sia soddisfatta M deve essere negativo. Si è così
verificato che effettivamente il segno di M dipende dal senso di avvolgimento delle spire intorno al
materiale magnetico. In pratica si tiene conto del senso di avvolgimento delle spire contrassegnando
una delle estremità di ciascun avvolgimento. Viene poi utilizzata la seguente convenzione:
se le corrente nei due induttori accoppiati entrano o escono contemporaneamente dai due
contrassegni allora si avrà M>0:
9
Se invece la corrente in un induttore entra (esce) e la corrente del secondo induttore accoppiato esce
(entra) dal contrassegno, sarà M<0:
Regola della mano destra: se si avvolgono le dita della mano destra intorno alla bobina, nel verso
della corrente, il flusso generato da tale corrente ha il verso indicato dal pollice.
Induttori a tre porte
La generalizzazione di quanto detto sinora al caso di un induttore a tre porte (o anche ad n porte) è
banale. Esso sarà costituito da tre avvolgimenti sovrapposti (che comunque si disegnano
separatamente) come mostrato in figura:
La sua caratteristica può essere posta in forma matriciale come segue:
⎡ Φ1 ⎤ ⎡ L11
⎢Φ ⎥ = ⎢ M
⎢ 2 ⎥ ⎢ 12
⎢⎣ Φ 3 ⎥⎦ ⎢⎣ M13
M12
L 22
M 23
M13 ⎤ ⎡ i1 ⎤
M 23 ⎥⎥ ⋅ ⎢⎢i 2 ⎥⎥
L33 ⎥⎦ ⎢⎣ i3 ⎥⎦
10
In questo caso per determinare il segno dei tre coefficienti di mutua induttanza bisognerà osservare
l’andamento delle correnti sulle tre porte prese due a due, ossia applicare la suddetta convenzione
alle porte 1 e 2 per trovare il segno di M12, alle porte 2 e 3 per trovare il segno di M23 e alle porte 1
e 3 per trovare il segno di M13.
TRASFORMATORE IDEALE
Un dispositivo fisico molto importante è il trasformatore reale, che viene generalmente utilizzato
per variare opportunamente tensione e corrente in uscita rispetto alla tensione e corrente in ingresso
a parità di potenza trasmessa. Per studiare il comportamento di questo elemento si fa riferimento a
un suo modello semplificato che prende il nome di trasformatore ideale e che si basa sulle seguenti
ipotesi semplificative:
1) non ci sono flussi dispersi;
2) non ci sono perdite (in particolare, non ci sono correnti parassite né perdite per isteresi e inoltre i
due avvolgimenti sono consideranti con resistenza nulla);
3) il materiale magnetico è costituito da una permeabilità infinita e la sua struttura è filiforme.
Per le ipotesi fatte, si può ritenere che:
• le linee di flusso del campo magnetico generato dalle correnti nei due avvolgimenti siano
contenute tutte all’interno della struttura;
• il campo magnetico sia costante lungo ogni cammino chiuso scelto all’interno della
struttura;
• il flusso del campo magnetico risultante attraverso una generica sezione S del trasformatore
ideale sia costante per ogni sezione, non essendoci flussi dispersi.
Si consideri la rappresentazione di questo elemento circuitale riportata di seguito.
In riferimento a questa rappresentazione e sulla base delle precedenti considerazioni, si può
scrivere:
⎧Φ1 = N1ϕ
⎨
⎩Φ 2 = N 2ϕ
11
dove ϕ è il flusso del campo magnetico generato dalle correnti nei due avvolgimenti, Φ1 è il flusso
totale concatenato al primo avvolgimento, Φ 2 è il flusso totale concatenato al secondo
avvolgimento.
Tenendo poi presente che le resistenze dei due avvolgimenti sono nulle (e quindi non si hanno su di
essi cadute di tensione) con l’applicazione della legge di Faraday si ottiene:
dΦ1
dϕ
⎧
⎪⎪ v1 = dt = N1 dt
⎨
⎪ v = dΦ 2 = N dϕ
2
⎪⎩ 2
dt
dt
⇒
v2 N 2
=
=n
v1 N1
dove n è detto rapporto di trasformazione ed evidentemente può essere un numero maggiore o
minore di 1.
Questa equazione fornisce, per l’elemento considerato, la relazione che esiste tra le tensioni ai capi
dei due avvolgimenti.
Se ora si applica il teorema di Ampere al cammino medio Γ di lunghezza L e sempre considerando
le ipotesi precedenti, si ottiene:
v∫ H ⋅ d l = N1i1 + N 2i 2 ⇒ HL = N1i1 + N 2i 2
Γ
⇒
B
μ
L = N1i1 + N 2i 2 ⇒
L
ϕ = N1i1 + N 2i 2
μS
Nell’ultima espressione considerata si può notare che L, S e ϕ sono quantità costanti e di valore
finito, mentre μ è infinita per ipotesi, e si può scrivere:
N1i1 + N 2i 2 = 0 ⇒
i2
N
1
=− 1 =−
i1
N2
n
Questa equazione fornisce, per l’elemento considerato, la relazione che esiste tra le correnti nei due
avvolgimenti.
Nota: questa dimostrazione si può fare in modo più semplice se si fanno le seguenti considerazioni a partire dalla
formula B = μ H , infatti è sufficiente considerare che se si considera, come già detto nelle ipotesi, una permeabilità
infinita allora deve accadere che H sia nullo nel mezzo considerato, poiché solo in questo modo si può ottenere un
campo di induzione magnetica B di valore finito all’interno del mezzo e B deve avere valore finito poiché si è supposto
che nel mezzo ci sia un flusso magnetico finito e costante.
Le due equazioni considerate contemporaneamente definiscono il comportamento del trasformatore
ideale e vengono scritte nella forma seguente:
⎧ v 2 = nv1
⎪
⎨
1
⎪⎩i 2 = − n i1
⇔
⎡ 0
⎡ v2 ⎤ ⎢
⎢ ⎥= 1
⎣ i2 ⎦ ⎢−
⎣ n
n⎤
⎥ ⋅ ⎡ i1 ⎤
⎢ ⎥
0 ⎥ ⎣ v1 ⎦
⎦
Mediante queste equazioni si ottiene facilmente la seguente interpretazione circuitale equivalente
del trasformatore ideale:
12
i1
i2
+
v1
v2/n
+
–
–
-i1/n
+
v2
–
Si noti che queste relazioni sono “istantanee” ossia nota una variabile si ottiene immediatamente il
valore dell’altra senza dover conoscere il valore iniziale della stessa e l’andamento del tempo della
variabile corrispondente, come accade per gli induttori o i condensatori, per cui il trasformatore
ideale è di fatto un elemento resistivo. In particolare e come d’altronde si nota dal suo equivalente
circuitale si tratta di un resistore biporta.
Il simbolo circuitale di un trasformatore ideale è:
Proprietà del trasformatore ideale
Il trasformatore ideale gode delle seguenti proprietà:
1) è un elemento non energetico ovvero è trasparente rispetto alla potenza; infatti se si calcola la
potenza istantanea per un trasformatore, considerando la definizione di potenza per un elemento
biporta, si ha:
p(t) = v1 (t)i1 (t) + v 2 (t)i 2 (t) = v1 (t)i1 (t) -
i1 (t)
( nv1 (t) ) = 0
n
2) se si collega alla porta 2 un resistore di resistenza R, la porta 1 si vede una resistenza equivalente
R
pari a 2 dove n è il rapporto di trasformazione.
n
Per dimostrare quanto sopra si consideri la situazione circuitale rappresentata nella figura in basso.
13
In questo caso si ha:
⎧ v 2 = nv1
⎪
v R = v 2 ; i 2 = −i R e ricordando la relazione di lato del Trasformatore ideale: ⎨
1
⎪⎩i 2 = − n i1
si ottiene:
1
1
1
1
1 ⎛ 1 ⎞ 1
v1 = v 2 = v R = Ri R = R ( −i 2 ) = R ⎜ − i1 ⎟ = 2 Ri1
n
n
n
n
n ⎝ n ⎠ n
v
essendo poi per definizione R1 = 1 la resistenza equivalente alla porta 1 resta dimostrato quanto
i1
detto.
3) se si collega alla porta 1 un resistore di resistenza R, la porta 2 si comporta come un resistore di
resistenza pari a: n 2 R dove n è il rapporto di trasformazione.
Per dimostrare quanto sopra si consideri la situazione circuitale rappresentata nella figura in basso.
In questo caso si ha:
⎧ v 2 = nv1
⎪
v R = v1 ; i1 = −i R e ricordando la relazione di lato del Trasformatore ideale: ⎨
1
⎪⎩i 2 = − n i1
si ottiene:
v 2 = nv1 = nvR = nRiR = nR ( −i1 ) = nR ( ni2 ) = n 2 Ri 2
essendo poi per definizione R 2 =
v2
la resistenza equivalente alla porta 2 resta dimostrato quanto
i2
detto.
Pertanto, il trasformatore ideale è in grado di operare quella che viene detta trasformazione delle
impedenze, infatti quanto dimostrato ai punti 2) e 3) vale anche in regime sinusoidale se si
considera un’impedenza collegata alla porta 1 o 2 del trasformatore.
14
Esempio
(Perfetti E.12 p. 464)
Considerato il circuito disegnato in figura si valuti la tensione alla a-b.
Soluzione:
Le leggi di Kirchhoff che possono essere scritte per il seguente circuito sono:
v S = v R1 + v1 ; per la maglia a sinistra
v R 3 = v R 2 + v 2 ; per la maglia a destra
iR1 = i1 ; iR 2 = i2 ; iR 2 + iR 3 = 0 ; per l’equilibrio delle correnti.
Introducendo a questo punto, sia le relazioni di lato dei resistori, sia la relazione di lato del
trasformatore ideale si può scrivere:
per la prima equazione:
v S = R1iR1 + v1 → v S = R1i1 + v1
per la seconda equazione:
R 3iR 3 = R2iR 2 + v 2
-R 3iR 2 = R2iR 2 + v 2
→
⎛ 1 ⎞
⎛ 1 ⎞
- R 3 ⎜ − i1 ⎟ = R2 ⎜ − i1 ⎟ + nv1
⎝ n ⎠
⎝ n ⎠
→
→
⎛1 ⎞
⎛1 ⎞
R 3 ⎜ i1 ⎟ + R2 ⎜ i1 ⎟ = + nv1
⎝n ⎠
⎝n ⎠
-R 3i2 = R2i2 + nv1
→ v1 =
→
1
( R 3 + R2 ) i1
n2
considerando le ultime due equazioni ottenute si ha un sistema di due equazioni nelle incognite v1 e
i1 che può essere risolto semplicemente sostituendo l’espressione di v1 nella prima delle due
equazioni e si ha:
v S = R1i1 +
1
( R 3 + R2 ) i1
n2
da cui:
i1 =
vS
R1 +
1
( R 3 + R2 )
n2
15
che dal punto di vista numerico equivale a: i1 =
2
v S A.
9
1
1
1
e quindi: i2 = − i1 = − v S A e i3 = −i2 = v S A
9
9
n
ed infine il valore della tensione v ab , vab = v3 = R3i3 =
3
v S V.
9
TRASFORMATORE REALE
Il modello del trasformatore ideale è utile per approssimare bene il comportamento del
trasformatore reale in molti casi pratici. Tuttavia, se si vuole ottenere un modello più accurato del
trasformatore reale si devono rimuovere le ipotesi semplificative che sono state considerate in
precedenza ossia:
1) assenza di flussi dispersi (accoppiamento perfetto k=1)
2) assenza di perdite:
2.1 correnti parassite;
2.2 perdite per isteresi;
2.3 resistenza non nulla dei conduttori.
3) permeabilità infinita (µ→∞).
La rimozione della ipotesi 3) porta a dire che la riluttanza magnetica del nucleo deve essere diversa
L
da zero, come si nota dalla stessa definizione di riluttanza magnetica: ℜ =
.
μS
L
Inoltre, dalla relazione
ϕ = Ni ⇒ ℜϕ = Ni , ottenuta considerando una sola bobina avvolta N
μS
volte su un supporto ferromagnetico, si deduce che la corrente di induzione magnetica che produce
il flusso ϕ non può più essere considerata praticamente nulla come accade quando si considera
ℜ ≈ 0 ; ci deve essere, quindi, una corrente di magnetizzazione di valore finito nel primario per
produrre il flusso di induzione.
Il problema, quindi, è quello di identificare questa corrente.
Nel trasformatore ideale la relazione che esiste tra le tensioni di porta e il flusso che si instaura nella
struttura considerata è data da:
dΦ1
dϕ
⎧
⎪⎪ v1 = dt = N1 dt
v
N
⇒ 2 = 2 =n
⎨
v1 N1
⎪ v = dΦ 2 = N dϕ
2
2
⎪⎩
dt
dt
che nel caso in cui si supponga di essere in regime sinusoidale porta alle relazioni:
16
⎪⎧V 1 = jϖ N1ϕ
⎨
⎪⎩V 2 = jϖ N 2ϕ
a seguito di questa relazione, si comprende come il flusso nel trasformatore sia sinusoidale nel
tempo e con questo lo è anche la corrente di magnetizzazione del primario, infatti il flusso è
proporzionale al campo di induzione magnetica attraverso la relazione ϕ = BS essendo S la
superficie tagliata dal flusso magnetico, mentre B è proporzionale al campo magnetico attraverso la
permeabilità magnetica ( B = μ H ), infatti nell’ipotesi che la permeabilità magnetica sia elevatissima
fa si che questa relazione che descrive il ciclo di isteresi sia lineare. Infine, la corrente è
proporzionale al campo magnetico attraverso la relazione HL = Ni che si ottiene dall’applicazione
del Teorema di Ampere, essendo L la lunghezza del percorso considerato.
Nel trasformatore reale invece l’assunzione di una permeabilità magnetica finita fa perdere la
linearità della relazione B = μ H che diventa non lineare secondo il tipo di ferro considerato e
quindi secondo la relazione propria del ciclo di isteresi per quel materiale. Come conseguenza la
corrente di magnetizzazione del primario risulta non lineare.
Questa corrente non lineare, però, può essere sviluppata secondo lo sviluppo in serie di Fourier in
una somma di sinusoidi, secondo una delle due forme equivalenti:
iϕ (t ) = 2 ⎡⎣ I1' sin(ωt ) + I 3' sin(3ωt ) + I 5' sin(5ωt ) + ...I1'' cos(ωt ) + I 3'' cos(3ωt ) + I 5'' cos(5ωt ) + ...⎤⎦
iϕ (t ) = 2 [ I1 cos(ωt + α1 ) + I 3 cos(3ωt + α 3 ) + I 5 cos(5ωt + α 5 ) + ...]
La seconda espressione degli sviluppi in serie di Fourier è utile quando è possibile, come nel caso
dei trasformatori di potenza, trascurare l’errore che si ha quando si assume la corrente
magnetizzante coincidente con la prima armonica: iϕ (t ) = 2 I1 cos(ωt + α1 ) .
In alternativa si può considerare la prima espressione degli sviluppi in serie di Fourier. In questo
caso si tiene conto dell’effettiva forma della corrente e si assume la corrente magnetizzante avente
la seguente espressione: i10 (t ) = 2 I10 cos(ωt + ϕ10 )
detta corrente a vuoto convenzionale e dove I10 =Iϕ =
(I ) +(I )
'
1
2
'
3
2
( ) +(I )
+ ... I1''
2
''
3
2
+ ...
è il valor efficace della corrente iϕ (t ) .
La corrente i10 (t ) è caratterizzata imponendo che essa abbia:
a) lo stesso valore efficace della corrente magnetizzante effettiva iϕ (t )
b) produca la stessa potenza media dissipata nel nucleo del trasformatore.
In questo modo, è possibile ancora utilizzare il metodo dei fasori per la determinazione di un
circuito equivalente del trasformatore reale che tenga conto della permeabilità finita.
Prima di fare questo, però, si assumano le seguenti convenzioni per il trasformatore ideale.
Si consideri la struttura di seguito:
17
Con i versi delle correnti e degli avvolgimenti scelti, il flusso generato segue il verso segnato in
figura per entrambi gli avvolgimenti, pertanto le forze elettromotrici indotte che si oppongono alle
variazioni di flusso hanno i versi esattamente i versi segnati in figura.
In questo caso le relazioni che si hanno tra le f.e.m. e i flussi che le generano sono date dalle
espressioni:
dΦ1
dϕ
⎧
⎪⎪e1 = − dt = − N1 dt
⎨
⎪e = − dΦ 2 = − N dϕ
2
⎪⎩ 2
dt
dt
essendo, come al solito, unico il flusso nella struttura del trasformatore ideale.
A questo punto, si nota come, questa scelta coincida con lo scegliere la convenzione del generatore
a ciascuna delle due porte del trasformatore. In particolare, se si assumono con E1 e E2 le due
f.e.m. al primario e al secondario del trasformatore in regime sinusoidale, rispettivamente, e il
1
parametro a = per definire il rapporto spire tra il primario e il secondario del trasformatore,
n
considerando il simbolo circuitale del trasformatore si ha:
I1
I2
E1
E2
E’ comunque da sottolineare che le f.e.m considerate non modificano di fatto la relazione di lato del
trasformatore considerate che è ovviamente sempre:
1
⎧
⎪V2 = V1
a
⎨
⎪ I = −a I
1
⎩2
essendo tensioni e correnti definite come fatto inizialmente secondo la convenzione dell’utilizzatore
ad entrambe le porte del trasformatore, ossia secondo quanto mostrato nella figura in basso.
18
I2
I1
V1
V2
questo dovrebbe rendere più chiara la differenza esistente tra le variabili di porta per descrivere da
un punto di vista circuitale il trasformatore ideale e le f.e.m. indotte in funzione, è ovvio, dei versi
di corrente e flusso di induzione magnetica.
In questo modo, inoltre, riprendendo lo schema seguendo le nuove convenzioni è possibile
distinguere tra le variabili di porta del trasformatore ideale e quelle del modello circuitale del
trasformatore reale, come è più evidente dallo schema sottostante dove il trasformatore ideale è
racchiuso nel rettangolo.
I1
+
V1
I2
a:1
E1
+
+
E2
V2
+
Guardando quest’ultimo schema diventa evidente che la relazione esistente tra le f.e.m. indotte le
variabili di porta e il flusso di induzione magnetica è espressa secondo la seguente relazione:
⎧⎪V 1 = − E1 = jϖ N1ϕ
⎨
⎪⎩V 2 = E 2 = − jϖ N 2ϕ
e, supponendo di rappresenta il flusso di induzione magnetica nel piano di Gauss con i fasori (si è
già detto che anche il flusso è variabile nel tempo con legge sinusoidale) si può ottenere il seguente
diagramma fasoriale.
− E1 = V1
E2 = V2
ϕ
Questo ci consente di comprendere meglio significato fisico della corrente magnetizzante.
Infatti, assunta per essa l’espressione i10 (t ) = 2 I10 cos(ωt + ϕ10 ) sinusoidale essa può essere
rappresentata nel diagramma precedente nel seguente, modo:
19
− E1 = V1
E2 = V2
ϕ10
ϕ
I10
Pertanto la corrente I10 può essere divisa nelle due componente in fase e in quadratura rispetto alla
tensione V1 . Dette I a e I m queste due componenti. rispettivamente, nella rappresentazione fasoriale
si ha:
− E1 = V1
E2 = V2
ϕ10
Im
I10
Ia
ϕ
Con questa scomposizione è comodo calcolare la potenza complessa al primario del trasformatore
quando il secondario è a vuoto. In questa condizione la corrente assorbita dal primario coincide con
la corrente di magnetizzazione e si ha:
N = V1 I1∗ = V1 I10∗ = V1 ( I a − jI m ) = V1 I a + jV1 I m = Pa + jQm
∗
Si nota, quindi, che la corrente I a fa riferimento ai fenomeni relativi alla dissipazione di potenza
nel primario, infatti da essa dipende la potenza attiva al primario ed è per questo che viene detta
componente attiva della I10 , mentre la corrente I m fa riferimento alla potenza scambiata, ma non
dissipata dal primario e quindi alla potenza reattiva, essa è pertanto detta corrente di
magnetizzazione della I10 .
In definitiva, la prima corrente tiene conto dei fenomeni dissipativi nel trasformatore, la seconda
tiene conto della corrente finita necessaria per mantenere un flusso finito nel trasformatore.
Da un punto di vista di modello circuitale si tiene conto della corrente I10 inserendo in parallelo al
primario del trasformatore un’ammettenza di opportuno valore di conduttanza e suscettanza, ossia:
G=
Pa
V12
e
B=
Qm
.
V12
Il circuito equivalente a questo punto diventa:
20
I1
+
V1
Ia
G
I2
a:1
I10
Im
B
E1
+
+
E2
V2
+
Sino a questo punto si è parlato di perdite nel condensatore e si è detto che queste perdite sono
espresse dalla conduttanza G, si cerca a questo punto di valutare con maggior dettaglio quello che
accade dal punto di vista fisico in relazione a quelle che vengono dette perdite nel ferro.
PERDITE NEL FERRO
Perdite per correnti parassite
Consideriamo una lamina di ferro (Fe) di dimensioni b x h x l con b di dimensioni trascurabili
rispetto ad h ed l, sulla quale é avvolto un avvolgimento costituito da N spire conduttrici di
resistenza trascurabile e ai cui capi é applicata una tensione v variabile nel tempo:
La corrente i nell’avvolgimento genera un campo di induzione magnetica B che, secondo la
regola del cavatappi, é entrante nel piano del foglio. Di conseguenza c’é un flusso dell’induzione
magnetica che si concatena con la generica sezione trasversale S della lamina:
ϕ = BS
21
Se la tensione v(t) varia nel tempo, varia anche la corrente i (t) e il campo di induzione magnetica
B e quindi anche il flusso dell'induzione ϕ (t ) é variabile nel tempo.
Se si suppone che la lamina di ferro sia costituita da tante lamine cave elementari e concentriche di
spessore infinitesimo dx e lunghezza l, che l’altezza di tali lamine cave sia comunque h e la loro
base trascurabile rispetto all’altezza, si può assumere che la lunghezza del contorno llamina sia:
llamina = 2h + 2b ≅ 2h
Sia Φ x il flusso di induzione magnetica che si concatena con la generica lamina cava elementare
individuata dall’ascissa x. Il flusso Φ x , che é variabile nel tempo, induce una f.e.m nella lamina
cava. Tale f.e.m é, a sua volta, responsabile di una corrente indotta ip nella lamina cava.
Il verso della corrente indotta ip deve essere tale da opporsi alla causa che l’ha generata, pertanto se
il flusso Φ x aumentando nella direzione entrante nel piano del foglio, la corrente indotta ip deve
generare un flusso di induzione opposto a Φ x e quindi uscente dal piano del foglio. Pertanto, il
verso di ip é immediatamente determinato con la regola del cavatappi ed è quello antiorario sulla
lamina come indicato in figura.
La corrente ip prende il nome di corrente parassita ed é responsabile delle così dette perdite per
correnti parassite che possono essere valutate nel modo seguente.
La tensione, supposta sinusoidale, v(t) applicata alla bobina che produce in campo B deve
eguagliare la caduta di tensione dovuta alla resistenza propria del materiale di cui è costituito
l’avvolgimento Ravv. e la forza elettromotrice prodotta dalla variazione del flusso di induzione
magnetica, quindi si ha:
dϕ
dϕ
+ Ravv.i (t ) ≅ N
dt
dt
essendo ϕ il flusso concatenato con una spira dell’avvolgimento e supponendo che la resistenza
dell’avvolgimento sia trascurabile.
Pertanto, si può affermare che sia il flusso ϕ , sia il flusso Φ x che attraversa una singola lamina di
dimensioni dx sono funzioni sinusoidali del tempo e possono essere ricavati dalle seguenti
espressioni:
v(t ) = −e(t ) + Ravv.i (t ) = N
ϕ = BS , Φ x = B 2hx
mentre dal punto di vista grafico essi sono espressi come segue:
22
Sia B ( t ) = BM sin ωt l’espressione nel tempo del campo B nella lamina, il flusso di induzione
magnetica nella singola lamina cava assume la forma:
Φ x = 2hxBM sin ωt
mentre la forza elettromotrice indotta è data da:
dΦx
ex ( t , x ) = −
= −2hxω BM cos ωt
dt
a questo punto si può calcolare la potenza dissipata per effetto Joule in questa singola lamina. Essa
sarà data, essendo la propagazione di tipo sinusoidale, dal rapporto tra il quadrato del valor efficace
della tensione a cui è sottoposta la singola lamina cava e la resistenza che essa offre al passaggio
della corrente generata da tale tensione, ossia:
Ex2
rx
essendo Ex il valor efficace della f.e.m indotta e rx la resistenza opposta dalla lamina elementare al
passaggio di corrente.
dP =
Il valor efficace della f.e.m indotta si può ottenere per definizione di valor efficace dall’espressione:
Ex =
2
E
1
⎡⎣ ex ( t ) ⎤⎦ dt = Mx
∫
TT
2
dove la EMx è il valor massimo della f.e.m. indotta e si ottiene facilmente dalla seguente
espressione:
EMx = max ⎡⎣ ex ( t , x ) ⎤⎦ = max [ −2hxω BM cos ωt ] = −2hxω BM
mentre rx si ottiene dalla formula:
23
rx =
ρ fellamina
ldx
con ρ fe la resistività specifica del ferro, poiché la corrente ip attraversa la superficie trasversale della
lamina data da ldx per tutta la sua lunghezza. In definitiva, si ha:
E 2 ( −2hxω BM ) ldx ( −2hxω BM ) ldx hlω 2 BM2 x 2 dx
dP = x =
=
=
2
2
rx
ρ fe
2 ρ l
2 ρ 2h
2
( )
2
( )
fe lamina
fe
Se si vuole conoscere la potenza dissipata nell’intera lamina iniziale a questo punto è possibile
integrare rispetto alla dimensione x la potenza appena calcolata.
b /2
b /2
P = ∫0 dP = ∫0
hlω 2 BM2 x 2
ρ fe
dx =
hlω 2 BM2
ρ fe
b /2
b /2
∫0
⎤
hlω 2 BM2 ⎡ x 3
hlω 2 BM2
−
=
0
x dx =
⎥
ρ fe ⎢⎣ 3
ρ fe
⎦0
2
⎡ b3 ⎤ hlb 2ω 2 BM2
⎢ ⎥=
24 ρ fe
⎣ 24 ⎦
e ricordando che hlb corrisponde al volume della lamina considerata si può definire la potenza
dissipa per unità di volume.
PF =
P b 2ω 2 BM2 4π fb 2 BM2 π 2 f 2b 2 BM2
=
=
=
vol
24 ρ fe
24 ρ fe
6 ρ fe
considerando direttamente il valore della frequenza f della tensione v(t) e non la sua pulsazione.
Da quanto visto in precedenza si può dedurre che la potenza dissipata nel ferro a seguito delle
correnti parassite sono inversamente proporzionali alla resistività ρ fe , di conseguenza un modo per
ridurle consiste nel cercare di aumentare ρ fe introducendo delle impurità a base di silicio.
La percentuale di tali impurità non supera il 2% ~4% in quanto si avrebbe un aumento inaccettabile
della fragilità dei lamierini che, nella costruzione delle macchine elettriche, vengono sottoposti a
processi di lavorazione per i quali si richiede malleabilità e duttilità.
Un altro fattore su cui si può agire per ridurre le ρ fe é lo spessore b dei lamierini: costruendo dei
lamierini molto sottili (0.5 mm. - 0.35 mm.) si riesce a ridurre discretamente le perdite per correnti
parassite nel ferro.
Dalla formula della potenza. si osserva, inoltre che a frequenze elevate corrispondono perdite
elevate.
Perdite per isteresi
Oltre alle perdite per correnti parassite, i lamierini di ferro che costituiscono le macchine elettriche
sono interessati alle perdite per isteresi dipendenti dalle proprietà magnetiche del ferro.
Microscopicamente, le sostanze ferromagnetiche sono costituite da dipoli magnetici ognuno dei
quali presenta un suo momento di dipolo magnetico.
Tali dipoli magnetici sono inseriti in entità più grandi del livello atomico dette dominii di Weiss.
Ciascun dominio é costituito da tanti dipoli magnetici i cui momenti di dipolo sono orientati tutti
nella stessa direzione e che sommandosi danno luogo ad un unico momento magnetico risultante.
24
Nel ferro vergine (mai sottoposto ad alcuna sollecitazione elettromagnetica) i momenti magnetici
associati ai dominii di Weiss sono orientati casualmente sicché il loro contributo totale é nullo.
In queste condizioni il ferro non mostra nessuna proprietà magnetica a livello macroscopico.
Sottoponendo un nucleo ferroso all’azione di un campo magnetico, accade che i momenti magnetici
associati ai dominii di Weiss tendono a orientarsi nella direzione del campo: a questo punto il loro
contributo totale non é più nullo ed il nucleo ferroso mostra un momento magnetico macroscopico.
Si dice che il nucleo ferroso si é magnetizzato.
Inizialmente, all’aumentare del campo magnetico H l’induzione magnetica B , che é un indice
dello stato di magnetizzazione del nucleo, aumenta proporzionalmente sicché il legame tra H e B
é lineare. Continuando ad aumentare il valore del campo H , man mano che il nucleo ferroso si
avvicina allo stato di saturazione nel quale tutti i dominii di Weiss sono tutti orientati nella
direzione di H , la magnetizzazione del nucleo aumenta sempre più lentamente e il legame tra H e
B non é più lineare.
Giunti alla saturazione, se si diminuisce il campo H fino a ridurlo a zero, il nucleo ferroso non si
smagnetizza del tutto, ma presenta una magnetizzazione residua che può essere annullata
applicando un campo -H opposto a quello di partenza (campo coercitivo -Hc).
Se si aumenta tale campo -H opposto a quello di partenza, ad un certo punto si raggiungerà la
saturazione opposta e da qui, diminuendo il campo fino ad annullarlo ci sarà una magnetizzazione
residua opposta che per poter essere annullata necessita dell’applicazione di un campo coercitivo Hc
... e cosi via fino a chiudere il ciclo.
Se si diagrammano i valori di B in funzione di H si ottiene, per quanto detto, un andamento di
questo tipo:
Tornando alla lamina di ferro su cui é avvolta la bobina costituita da N spire, essendo la corrente
nella bobina sinusoidale, anche il campo H da essa generato é sinusoidale e di conseguenza tale
lamina subisce un ciclo di magnetizzazione come quello descritto , cioè effettua un ciclo di isteresi.
La realizzazione di tale ciclo di magnetizzazione comporta un consumo di energia necessario per
vincere le forze di attrito che si sviluppano tra i dominii di Weiss quando questi ultimi scattano per
orientare il loro momento magnetico concordemente alla direzione del campo H .
25
Nelle macchine elettriche, l’energia necessaria per realizzare un ciclo di isteresi prende il nome di
perdite per isteresi. Si cerca ora di valutare l’energia necessaria per effettuare il ciclo di isteresi.
L’energia assorbita dall’avvolgimento può essere valutata integrando la potenza:
t1
t1
0
0
w(t0 , t1 ) = ∫t p (t )dt = ∫t v(t ) ⋅ i (t )dt
nel caso in esame la tensione è data da:
dϕ
dϕ
+ Ravv.i (t ) ≅ N
dt
dt
essendo ϕ il flusso concatenato con una spira dell’avvolgimento e supponendo che la resistenza
dell’avvolgimento sia trascurabile, come visto in precedenza. Pertanto, la valutazione dell’energia
infinitesima, si può fare considerando il contributo:
v(t ) = −e(t ) + Ravv.i (t ) = N
dϕ
i (t )dt = Ni (t )dϕ
dt
infine, ricordando che: ϕ = BS e che v∫ H ⋅ d l = Ni ⇒ Hl = Ni la formula precedente assume la
dw(t0 , t1 ) = v(t ) ⋅ i (t )dt = N
l
forma:
dw(t0 , t1 ) = Ni (t )dϕ = Hldϕ = hlSdB = volHdB
infatti, la quantità Sl esprime il volume della lamina considerata.
La quantità di energia per unità di volume, che serve per compiere il ciclo di isteresi, si può così
ottenere integrando l’energia infinitesima tra i valori che assume il campo B tra gli istanti di tempo
t0 e t1 che poi sono i valori che determinano il periodo della sinusoide della tensione di ingresso,
ossia se si assume che sia t0=0 e t1=T. In definitiva, si ha:
B1
w(t0 , t1 )
= ∫B HdB
0
vol
Nel caso in cui si assume che ci sia linearità tra i valori dei campi H e B ossia cha valga la
relazione: B = μ H è particolarmente semplice risolvere l’integrale precedente e si ha:
B1
B1 B
w(t0 , t1 )
1 B 2 1 BB 1 Bμ H 1
= ∫B HdB = ∫B dB =
=
=
= BH
0
0 μ
2 μ 2 μ
2 μ
2
vol
Questa espressione dell’energia fa comprendere come l’energia per unità di volume assorbita dal
materiale di cui è fatto il nucleo del trasformatore sia graficamente rappresentata dall’area racchiusa
dal ciclo di isteresi.
Per comprendere meglio questo concetto, si può focalizzare l’attenzione sulla prima parte del ciclo
di isteresi. Se si parte da un campo nullo e si prosegue sulla curva di prima magnetizzazione,
l’energia richiesta per unità di volume è quella sottesa alla curva, ossia è data dall’area compresa tra
la curva di prima magnetizzazione e l’asse delle ordinate (campo B ). Se poi si diminuisce il valore
del campo magnetico il punto di lavoro si muove sulla curva superiore del ciclo di isteresi per cui
l’energia che viene restituita è quella che corrisponde all’area sottesa a quest’ultima curva e quindi
compresa tra questa curva e l’asse delle ordinate (campo B ). A questo punto è chiaro come
l’energia che viene restituita, è solo quella rappresentata da quest’area che è chiaramente più
piccola di quella precedente. La differenza tra le due aree è l’energia dissipata nel materiale sotto
forma di calore. E’ per questo motivo che un materiale sottoposto a magnetizzazione alternativa
26
sinusoidale si riscalda, si parla quindi di energia perduta per isteresi in ogni ciclo. E’, inoltre,
intuitivo come le perdite per isteresi dipendano linearmente dalla frequenza.
Questa energia può essere calcolata come mostrato in precedenza, mentre nel caso in cui non ci sia
linearità dei campi H e B possono essere usate delle formule empiriche per calcolarla. Tra le più
note c’è la formula di Steinmetz:
wist = η BMn
dove η è un coefficiente che dipende dal particolare materiale considerato, mentre n è un numero
scelto empiricamente che può assumere valori da 1.5 a 2.5, in molti casi è usato il valore di 1.6.
A questo punto è possibile calcolare le perdite complessive nel ferro come somma delle perdite
dovute alle correnti parassite e quelle per isteresi, ossia come:
P = PF vol + Pist vol
dovendo moltiplicare le potenze per il volume effettivo del nucleo considerato.
In definitiva, considerando che la potenza spesa nel ciclo di isteresi si può calcolare a partire
w
η Bn
dall’energia dividendola per il periodo della sinusoide della tensione di ingresso ( Pist = ist = M ),
T
T
si ha:
P=
π 2 f 2b 2 BM2
η B n vol π 2 f 2b 2 BM2
vol + M
vol + η fBMn vol
=
T
6 ρ fe
6 ρ fe
Infine, si può notare, che l’energia complessivamente dissipata nel ferro é proporzionale alla
frequenza f. All’aumentare di f aumenta l’energia dissipata, inoltre per f=0 l’energia
complessivamente dissipata si riduce alla sola energia dissipata per isteresi.
A questo punto ci si pone un ultimo quesito circa le perdite nel ferro, ossia se queste perdite
dipendono dalla temperatura.
27
La risposta é affermativa se si considerano le perdite per correnti parassite e quelle per isteresi
singolarmente.
Globalmente, invece, si può affermare che, con buona approssimazione, le perdite nel ferro non
dipendono dalla temperatura. Infatti, se la temperatura aumenta, aumenta il moto di agitazione
termica dei domini di Weiss nel ferro e ciò facilita il loro orientamento nella direzione del campo:
minori forze di attrito, minore energia dissipata per vincerle, minori perdite per isteresi.
Al contrario, all’aumentare della temperatura aumenta la potenza dissipata per effetto Joule e
dunque aumentano le perdite per correnti parassite.
Tuttavia, dal punto di vista energetico, i due fenomeni si compensano sicché , globalmente, l’effetto
é nullo. Analogo discorso se la temperatura diminuisce.
Presenza del flusso disperso
Nella trattazione svolta sino a questo punto per giungere al modello del trasformatore reale si sono
rimosse le ipotesi di permeabilità infinita e di assenza di perdite, in particolare di perdite dovute alle
correnti parassite e perdite per isteresi. A questo punto, si può rimuovere l’ipotesi di assenza di
flussi dispersi.
Tonando alla trattazione generale di due induttori accoppiati, il flusso complessivo è stato calcolato
utilizzando quattro distinti contributi, come si seguito riportati.
ϕ11 = Λ11 N1i1 flusso dovuto a i1 che interessa solo il primo avvolgimento;
ϕ12 = Λ12 N1i1 flusso dovuto a i1 che interessa il primo ed il secondo avvolgimento;
ϕ21 = Λ 21 N 2i 2 flusso dovuto a i2 che interessa il primo ed il secondo avvolgimento;
ϕ22 = Λ 22 N 2i 2 flusso dovuto a i2 che interessa solo il secondo avvolgimento.
e i flussi per ciascuno dei due avvolgimenti sono stati calcolati considerando la somma di ciascuno
dei contributi ai due avvolgimenti ottenendo:
⎧Φ1 = Λ11 N12i1 + Λ12 N12i1 + Λ 21 N1 N 2i 2 = ( Λ11 N12 + Λ12 N12 ) i1 + Λ 21 N1 N 2i 2
⎪
⎨
2
2
2
2
⎪⎩Φ 2 = Λ12 N1 N 2i1 + Λ 22 N 2i 2 + Λ 21 N 2i 2 = Λ12 N1 N 2i1 + ( Λ 22 N 2 + Λ 21 N 2 ) i 2
questa espressione ha quindi consentito di giungere alla relazione caratteristica degli induttori
mutuamente accoppiati:
⎧Φ1 = L1i1 + Mi 2
⎨
⎩Φ 2 = Mi1 + L 2i 2
dove i coefficienti di auto e mutua induzione sono dati dalle seguenti espressioni:
L1 = N12 ( Λ11 + Λ12 ) , M = Λ 21 N1 N 2 = Λ12 N1 N 2 ,
L2 = N 22 ( Λ 22 + Λ 21 ) .
Quella che inizialmente è stata una suddivisione del flusso in modo da identificare i diversi
contributi ai due avvolgimenti, dei flussi prodotti separatamente dalle due correnti che li
attraversano, adesso può essere riconsiderata separando il flusso che interessa il primo e il secondo
avvolgimento dividendolo concettualmente in altri due contributi. Considerando ciascuno dei due
avvolgimenti si può individuare il flusso che interessa entrambi gli avvolgimenti e quello che
interessa uno solo dei due. In altri termini si può scrivere:
28
⎧Φ1 = Λ11 N12i1 + ( Λ12 N12i1 + Λ 21 N1 N 2i 2 )
⎪
⎨
2
2
⎪⎩Φ 2 = Λ 22 N 2i 2 + ( Λ12 N1 N 2i1 + Λ 21 N 2i 2 )
dove i contributi in parentesi corrispondono ai flussi che interessano entrambi gli avvolgimenti,
mentre i primi termini di ciascuna espressione è legata al flusso che interessa solo il primo ed il
secondo avvolgimento, rispettivamente.
A questo punto si comprende come i coefficienti di autoinduzione precedentemente definiti,
possano concettualmente essere anch’essi considerati costituiti da due contributi:
L1 = N12 Λ11 + N12 Λ12 , L2 = N 22 Λ 22 + N 22 Λ 21
individuando due termini e isolando in modo esplicito il termine che fa riferimento al così detto
flusso disperso in quanto interessa un solo avvolgimento e poi si chiedo in aria.
Definite le quantità: Lm = N12 Λ12 , L1d = N12 Λ11 , L2 d = N 22 Λ 22
i coefficienti di auto e mutua induzione e il coefficiente di accoppiamento possono essere quindi
riscritti secondo le seguenti espressioni:
L1 = L1d + Lm ,
L2 = L2 d + N 22 Λ 21 = L2 d +
M = Λ 21 N1 N 2 = Λ 21
k=
M
=
L1 L2
essendo n =
N 22 2
N 22
Λ
=
L
+
L = L2 d + n 2 Lm
N
d
1
21
2
2
2 m
N1
N1
N2 2
N = nLm
N1 1
nLm
( L1d + Lm ) ( L2 d + n 2 Lm )
N2
N1
In questa schematizzazione, L1d e L2d sono dette induttanze di dispersione del primario e del
secondario rispettivamente e risultano proporzionali al flusso disperso, mentre Lm è detta
induttanza di magnetizzazione ed è associata al flusso principale che si trova nel nucleo del
trasformatore.
E’ da sottolineare che mentre per Lm il calcolo del suo valore è piuttosto semplice poiché esso si
ottiene una volta calcolata la permeanza nel mezzo attraversato dal flusso principale con la formula
μS
Λ12 = Λ 21 =
, il calcolo delle induttanze L1d e L2d è molto più complesso, questo calcolo esula
l
comunque dalla presente trattazione.
Quanto fatto sino ad ora, ovviamente può essere riportato in regime sinusoidale per cui si ha:
⎪⎧V1 = jω L1 I1 + jω MI 2 = jω L1d I1 + jω L m I1 + jω nL m I 2
⎨
2
⎪⎩V2 = jω MI1 + jω L 2 I 2 = jω nL m I1 + jω L 2d I 2 + jω n L m I 2
ossia
29
⎧⎪V1 = jω L1d I1 + jω L m ( I1 + nI 2 )
⎨
⎪⎩V2 = jω L 2d I 2 + jω nL m ( I1 + nI 2 )
Questa trattazione ci consente di capire quali modifiche devono essere introdotte nel modello
circuitale del trasformatore ideale per giungere a quello reale. Infatti, le equazioni sopra possono
essere rappresentate attraverso il seguente schema circuitale.
I1
jϖ L1d
+
V1
I 2'
Im
jϖ Lm
B
jϖ L2d
a:1
E1
I2
+
+
E2
V2
+
La prima equazione corrisponde alla legge di Kirchhoff scritta per la maglia più a sinistra nello
schema e dove la corrente I 2' corrisponde alla corrente del secondario riportata al primario del
1
⎧
⎪V2id = V1id
si ha:
trasformatore ideale, infatti, dalle relazioni valide per i trasformatore ideale: ⎨
a
⎪ I = −a I
1id
⎩ 2id
1
I1id = − I2id = −n I2id da cui I2' = n I2id = n I2 , avendo I1id direzione opposta a I2' e essendo I2id
a
coincidente con I2' e dove il pedice id indica la differenza tra le tensioni e le correnti del
trasformatore ideale e quelle di porta del trasformatore reale.
Allo stesso modo, dallo schema circuitale si ha che la tensione V2 deve eguagliare la somma delle
tensioni sull’induttore di induttanza L2 d e tensione che si ha alla seconda porta del trasformatore
ideale. Ossia si ha:
1
V2 = jω L 2d I 2 + V2id = jω L 2d I 2 + V1id = jω L 2d I 2 + nV1id =
a
= jω L 2d I 2 + njω L m I m = jω L 2d I 2 + jω nL m ( I1 + nI 2 )
E’ evidente che questa seconda equazione corrisponde alla seconda espressione trovata in
precedenza.
In questa trattazione sono state trascurate le perdite, pertanto è necessario inserire nel circuito
appena ottenuto gli elementi che ne tengono conto. Le perdite dovute alle correnti parassite e alle
P
perdite per isteresi possono essere tenute in conto inserendo nel modello la conduttanza G = a2 ,
V1
come visto in precedenza. Esiste, però, un ultimo contributo da dover tenere in considerazione,
ossia quello dovuto alle perdite nel rame rilasciando così l’ultima ipotesi che era fatta per il
trasformatore ideale: resistenza nulla dei conduttori. Se si assume che i due valori di resistenza R1 e
R2 rappresentino le resistenze offerte dagli avvolgimenti del primario e del secondario
rispettivamente lo schema circuitale completo del trasformatore reale diviene:
30
I1
jϖ L1d
R1
+
I 2'
I10
Ia
V1
Im
B = jϖ Lm
G
jϖ L2d
a:1
E1
R2
I2
+
+
E2
V2
+
I valori delle grandezze che compaiono in questo schema dipendono dalla tipologia e
dall’applicazione del trasformatore. Tuttavia, si può affermare che la reattanza di magnetizzazione
ω Lm è molto maggiore delle reattanze di dispersione e delle resistenze degli avvolgimenti. Questo è
ovvio poiché rappresentano fenomeni indesiderati che nella costruzione dei trasformatori si cerca di
minimizzare. Inoltre, nei trasformatori di piccole dimensioni utilizzati ad esempio in applicazioni
audio, le potenze dissipate sono modeste sia per le basse tensioni di ingresso sia per i materiali usati
che hanno elevata permeabilità magnetica, ma bassa conducibilità. In questi casi la conduttanza G
può essere considerata nulla e le perdite sono associate alle sole resistenze degli avvolgimenti.
E’ evidente, comunque, che al contrario del trasformatore ideale la potenza dissipata dal
trasformatore reale non è nulla ed in particolare, anche nell’approssimazione di considerare
trascurabile la conduttanza G, vale:
2
2
P = R1 I1 + R2 I 2 .
Funzionamento sotto carico
Si consideri il circuito equivalente del trasformatore reale al quale è collegata al secondario una
generica impedenza di carico Z , come riportato nella figura in basso. In tale figura, inoltre, è stato
invertito, rispetto al circuito precedente, il verso della corrente I 2 e di conseguenza il verso della
corrente I 2' .
I1
+
V1
jϖ L1d
R1
Ia
G
I 2'
I10
Im
B = jϖ Lm
jϖ L2d
a:1
E1
R2
I2
+
+
E2
V2
Z
+
Ricordando quanto già fatto per il trasformatore ideale si ha:
v∫ H ⋅ d l = N1i1 + N 2i 2 ⇒ HL = N1i1 + N 2i 2
Γ
⇒
B
μ
L = N1i1 + N 2i 2 ⇒
L
ϕ = N1i1 + N 2i 2
μS
⇒ ℜϕ = N1i1 + N 2i 2
si deduce immediatamente che anche per il trasformatore reale si può scrivere la relazione:
31
ℜϕc = N1 I1 + N 2 I2
essendo I1 e I 2 le correnti al primario e secondario con i versi in figura, φc il flusso medio comune
e ℜ la riluttanza del circuito magnetico.
Ora, se si assume che φc e ℜ sia indipendenti dalle condizioni di carico si ha che la relazione sopra
può anche essere scritta nel caso di funzionamento a vuoto, ossia quando alla porta 2 non è
collegata alcuna impedenza. In questo caso, però, le correnti I1 e I 2 risultano entrambe nulle e
l’unica corrente esistente è la corrente a vuoto convenzionale I10 , pertanto la equivalente relazione
tra le correnti e il flusso medio comune è data da:
ℜϕc = N1 I10 .
Considerando le due espressioni precedenti si ha:
N1 I10 = N1 I1 + N 2 I2 .
Se si ricorda che la corrente del primario è data dalla somma della corrente a vuoto convenzionale
'
I10 e della corrente del secondario riportata al primario I 2' , ossia I1 = I10 + I2 , si può scrivere:
(
)
N1 I10 = N1 I10 + I2' + N 2 I2
da cui si deduce facilmente che:
I2' = −
N2
I2
N1
mentre
N2
I2 .
N1
Si nota quindi che nel trasformatore reale la presenza della corrente a vuoto convenzionale I10
impedisce di trovare un semplice rapporto tra le correnti al primario e al secondario.
Tuttavia in molti trasformatori la corrente I10 risulta essere percentualmente molto piccola rispetto a
I1 e I 2 , per cui non si commette un grosso errore se si assume il suo contributo nullo. In questo
caso si ha:
I1 = I10 −
N1 I1 + N 2 I2 ≈ 0
e si ha nuovamente un rapporto semplice identico a quello del trasformatore ideale tra le due
correnti I1 e I 2 :
I1
N
=− 2
I2
N1
Per quanto riguarda le tensioni, invece, riferendosi direttamente al circuito equivalente è facile
vedere che si ha:
32
⎪⎧V1 = − E1 + ( R1 + jX 1d ) I1
⎨
⎪⎩V2 = E2 − ( R2 + jX 2 d ) I 2
Da queste equazioni è facile vedere che anche il rapporto tra le tensioni è chiaramente diverso da
quello del trasformatore ideale, si ha infatti il seguente rapporto di trasformazione:
K=
V1 − E1 + ( R1 + jX 1d ) I1
N
=
≠ 1
V2
N2
E2 − ( R2 + jX 2 d ) I 2
Nel funzionamento a vuoto tuttavia si ha che la corrente al secondario è nulla mentre quella al
primario è data solo dalla corrente a vuoto convenzionale si ottiene:
K=
− E1
jω N1ϕ
V1 − E1 + ( R1 + jX 1d ) I10
N
=
≈
=
= 1
V2
− jω N 2ϕ N 2
E2
E2
Il penultimo passaggio si ottiene ricordando le espressioni delle tensioni del primario e secondario
del trasformatore ideale.
Reti equivalenti semplificate
Spesso piuttosto che utilizzare il circuito equivalente del trasformatore ideale così come ottenuto in
precedenza si usano circuiti a esso equivalenti ma più semplici, detti appunto reti equivalenti
semplificate del trasformatore reale.
Considerando il circuito ottenuto in precedenza collegando un carico alla porta 2 del trasformatore
si può ricavare il seguente circuito:
jϖ L1d
R1
I1
I10
Ia
V1
G
jϖ L '2 d
I 2'
Im
B = jϖ Lm
Z '
V2'
R2'
Tale circuito è ottenuto considerando le impedenze equivalenti viste al primario del trasformatore
ideale contenuto nel modello considerato. Si consideri, infatti, il circuito visto al primario del
trasformatore ideale come mostrato nella figura in basso.
I 2'
+
V2'
jϖ L2 d
a:1
E1
R2
I2
+
+
E2
V2
Z
+
33
L’impedenza vista al primario cioè la relazione tra il fasore della tensione V2' e il fasore della
corrente I 2' è data da
Z eq
n
2
dove Zeq = Z + R2' + jω L'2 d è l’impedenza complessiva collegata al
secondario del trasformatore ideale. Pertanto si ottengono le ovvie relazioni:
Z ' = Z / n 2 ,
X 2' d = jω L'2 d = jω L2 d / n 2 .
R2' = R2 / n 2 , L'2 d = L2 d / n 2 ,
Considerando che in genere le cadute sul primario del trasformatore reale sono piuttosto piccole. E’
possibile semplificare ulteriormente la rete, passando prima a un circuito nel quale la tensione
V1 del primario è direttamente applicata al ramo trasversale del modello e poi mettendo in serie le
resistenze e le reattanze del primario e del secondario.
+
I10
Ia
V1
+
Im
I 2'
I1
V1
jϖ L '2 d
I10
Ia
R2'
Re
Xe
+
Im
V2'
B = jϖ Lm
G
Z '
V2'
B = jϖ Lm
G
+
jϖ L1d
R1
I 2'
I1
Z '
Infine, nel caso in cui sia possibile trascurare anche la corrente a vuoto convenzionale I10 è
possibile eliminare nel modello il ramo trasversale ottenendo il seguente circuito.
I1
V1
Re
Xe
I 2'
V2'
Z '
In questo circuito l’impedenza costituita da Re e X e è normalmente indicata con Zcc = Re + X e e
prende il nome di impedenza di cortocircuito, mentre il coseno del suo argomento cos ϕcc prende il
nome di coseno di corto circuito.
34
In ultimo, quanto appena esposto può essere ripetuto se si riportano le grandezze del primario al
secondario, in questo caso con passaggi del tutto analoghi a quelli mostrati in precedenza si giunge
alla seguente rete equivalente con ovvio significato dei simboli riportati in figura.
I1''
R2e
X 2e
V1''
I2
V2
Z
Rendimento
Il rendimento di un trasformatore secondo la classica definizione di rapporto tra la potenza in uscita
rispetto a quella in ingresso è estremamente elevato, spesso si è vicini a 0.99. Questo rende difficile
da un punto di vista pratico considerare questa definizione per il rendimento di un trasformatore.
Infatti, in questo caso:
i) gli errori della strumentazione per calcolare le potenze in ingresso e in uscita potrebbero
essere tali da fornire valori di rendimento superiori all’unità;
ii) nel caso dei trasformatori più grandi con potenze anche dell’ordine dei MVA la misura
diretta sarebbe difficile perché si dovrebbe disporre di carichi adatti ad assorbire tali
potenze.
Pertanto in un trasformatore il rendimento detto rendimento convenzionale è dato dal rapporto tra la
potenza trasferita al carico e la somma della potenza trasferita al carico e quelle perdute nel rame e
nel ferro:
ηc =
V2 I 2 cos ϕ2
V2 I 2 cos ϕ2 + PCu + PFe
Se si esprimono le perdite nel rame in funzione della resistenza equivalente al secondario si ha:
PCu = Re 2 I 22 . Sostituendo questa espressione nella formula del rendimento si ha la formula dalla
quale è possibile calcolare la condizione che produce il massimo rendimento, imponendo che la
derivata del rendimento rispetto alla corrente I 2 sia nulla.
Questa condizione si verifica per PFe = Re 2 I 22 ossia quando le perdite nel Ferro sono identiche a
quelle nel rame ( PFe = PCu ). E’ evidente che tale condizione dipende dalla corrente del carico è
quindi importante comprendere come il rendimento dipenda da questa grandezza. Per far questo si
consideri I 2 n la corrente nominale del carico e Iη il valore della corrente I 2 per la quale si ottiene il
massimo rendimento, ossia proprio la corrente che soddisfa la condizione PFe = Re 2 Iη2 e di
conseguenza si ha:
Iη =
PFe
Re 2
allora si può definire il rapporto tra Iη e I 2 n :
35
λ=
Iη
I 2n
=
1
I2n
PFe
=
Re 2
PFe
=
Re 2 I 22n
PFe
PCun
essendo PCun la potenza persa nel rame nel caso in cui sia assorbita dal carico proprio la corrente
nominale.
Si noti che se le perdite nel ferro sono uguali a quelle nel rame quando il carico assorbe la corrente
nominale si ha λ = 1 , in questo caso la corrente che corrisponde al massimo rendimento è proprio
quella nominale. Tuttavia, mentre le perdite nel rame sono dipendenti dalla corrente I 2 , le perdite
nel Ferro sono di fatto dipendenti dalla tensione di alimentazione del trasformatore, pertanto il
P
P
rapporto Fe può essere diverso da 1. Ad esempio, se Fe = 0.8 si ha λ ≈ 0.89 il che vuol dire che
PCun
PCun
la corrente I 2 per cui si ha il massimo rendimento è l’89% di quella nominale, cioè Iη = 0.89 I 2 n . Se
il carico assorbe una corrente diversa da quella nominale il rendimento sarà inferiore a quello
massimo. Per tener conto di questa dipendenza è possibile considerare le curve che rappresentano il
P
I
rendimento proprio in funzione del rapporto 2 tracciate per fissato valore del rapporto Fe e
PCun
I 2n
fissato cos ϕ 2 . Un esempio qualitativo di queste curve è riportato nella figura in basso.
In questa figura la curva inferiore fa riferimento a
riferimento a
PFe
= 0.15 , mentre curva superiore fa
PCun
PFe
= 0.75 .
PCun
Per i trasformatori, inoltre si definisce anche il rendimento giornaliero, come:
ηg =
∑ i V2 I 2 cos ϕ2 Δti
∑ i V2 I 2 cos ϕ2 Δti + ∑ i Re 2 I 22 Δti + 24 PFe
dove gli intervalli di tempo Δti rappresentano i singoli intervalli in cui si può considerare il
trasformatore funzionante a pieno carico. In questo caso la condizione che deve essere soddisfatta
per ottenere il massimo rendimento è data da:
PFe
R I 2 Δti
∑
i e2 2
.
=
24
36
Prove sui trasformatori
Da quanto esposto in precedenza è possibile dedurre che per calcolare il rendimento di un
trasformatore le perdite nel Ferro e nel Rame sono parametri fondamentali. Dato un trasformatore
reale queste possono essere ricavate sperimentalmente effettuando due prove.
La prima prova è detta prova a vuoto. Essa è effettuata con lo schema di misura riportato in basso.
In questa prova ai morsetti del primario del trasformatore è applicata la tensione V1 , mentre i
morsetti del secondario sono lasciati aperti.
I10
+
V1
W
A
f
+
V1
V2
T
V2
In questa situazione di funzionamento nel trasformatore circola esclusivamente la corrente I10 , per
cui nel secondario non ci sono perdite, mentre quelle per effetto Joule nel primario possono ritenersi
trascurabili. Quindi, si può ritenere che ci siano solo le perdite nel Ferro le quali sono dipendenti
approssimativamente al quadrato della tensione V1 applicata in ingresso e al valore della frequenza
considerata per l’alimentazione.
In definitiva, si può ritenere valida la relazione P10 = PFe , essendo P10 le perdite dovute alla sola
corrente I10 , e la sua valutazione si ha semplicemente dalla misura del wattmetro W.
W = P10 = V1 I10 cos ϕ10
Gli ulteriori strumenti di misura indicati nella figura prima riportata, fanno poi riferimento alla
possibilità di sfruttare le condizioni operative di questa prova per identificare altre grandezza. Ad
esempio, le misurazioni dei due voltmetri V1 e V2, consentono di identificare il rapporto di
trasformazione, mentre la misura dell’amperometro consente di valutare il modulo della corrente
I10 che, con il contributo dello sfasamento rispetto alla tensione V1 fornisce i parametri G e B del
ramo trasversale del modello circuitale del trasformatore. Infatti, si ha:
cos ϕ10 =
P10
, I a = I10 cos ϕ10 ,
V1 I10
I m = I10 sin ϕ10 ,
G=
Ia
,
V1
B=
Im
.
V1
La seconda prova che si effettua è detta prova in cortocircuito. In questo caso la prova si effettua
secondo lo schema riportato nella figura seguente.
37
I1n
Vcc
I 2n
In questa prova i morsetti del secondario sono cortocircuitati mentre ai morsetti del primario del
trasformatore è applicata la tensione V1 che viene di solito indicata con Vcc ed è detta tensione di
cortocircuito. Questa è definita come la tensione che, con il secondario in cortocircuito, fa circolare
nel trasformatore le correnti nominali. Tale tensioni di solito risulta essere molto più bassa
(dell’ordine del 7-8%) di quella nominale. In questa situazione di funzionamento la corrente I10
diventa molto piccola, infatti essa è dipendente dalla tensione applicata al primario. Quindi, le
perdite nel trasformatore risultano essere solo quelle nel rame potendo trascurare quelle nel Ferro e
possono direttamente calcolarsi dalla lettura del wattmetro W.
W = Pcc = PCu = R 2e I 22
ricordando il circuito equivalente semplificato del trasformatore con i parametri riportati al primario
in cui le perdite nel rame sono tenute in conto dal resistore R 2e e in cui la corrente I 2 risulta essere
coincidente con quella in ingresso alla porta del circuito equivalente.
Gli ulteriori strumenti di misura indicati nella figura prima riportata, fanno poi riferimento alla
possibilità di sfruttare le condizioni operative di questa prova per identificare altre grandezza. In
questo caso, infatti le misurazioni dei due amperometri A1 e A2, consentono di identificare il
rapporto di trasformazione, mentre la misura del voltmetro consente di valutare il modulo della
tensione Vcc che permette di calcolare i parametri R 2e e X 2e del circuitale equivalente semplificato
del trasformatore con i parametri riportati al primario. Infatti, si ha:
R 2e =
Pcc
, Vcc = I 2 R 22e + X 22e .
2
I2
Parallelo di due trasformatori
Il servizio dell’utenza in bassa tensione (230V nel caso monofase, 400 V nel caso trifase) può
essere affidato a più di un trasformatore. Questo consente di garantire la continuità del servizio nel
caso di guasto di uno dei trasformatori (almeno due) e di farli funzionare in condizioni di pieno
carico, avendo di conseguenza un rendimento molto elevato. Infatti, nelle situazioni di carico ridotto
è possibile non far intervenire uno o più dei trasformatori presenti.
La connessione di più trasformatori deve essere fatta in parallelo, come riprodotto nella figura in
'
e
basso. In cui i due trasformatori sono caratterizzati dalle loro impedenze riportate al primario, Z 2e
Z '' e dai loro rispettivi rapporti di trasformazione n’ e n’’, mentre Z è l’impedenza che
2e
rappresenta il carico.
38
+V
1
+V
2
'
Z 2e
T’
Z
''
Z 2e
T’’
Per poter effettuare questa connessione devono, però, essere soddisfatte alcune condizioni:
a) la corrente a vuoto di ciascuno dei condensatori deve essere nulla;
b) la corrente erogata al carico si deve ripartire opportunamente tra i trasformatori;
c) il contributo di ciascuno dei trasformatori alla corrente del carico deve essere minimo.
Questa condizioni fanno riferimento alle necessità di:
a’) rendere nulle le perdite a vuoto;
b’) sollecitare i trasformatori in modo proporzionale alle relative potenze;
c’) minimizzare le perdite in condizioni di carico.
Considerata, quindi, la situazione precedente essa può essere ricondotta all’analisi del seguente
circuito equivalente:
Z 2' e
n 'V1
Z 2'' e
n ''V1
+
+
Z
–
I 2'
Iz
–
I 2''
dove i due generatori di tensione rappresentano il valore della tensione V2 che avrebbero i due
trasformatori al secondario in funzione dello specifico rapporto di trasformazione quando si ha in
ingresso la stessa tensione V1 . E’ facile vedere che in questo caso la corrente di circolazione a vuoto
è data da:
39
I 2' = − I 2'' =
n 'V1 − n ''V1
Z 2' e + Z 2'' e
da questa relazione è evidente che la condizione a) è soddisfatta solo nel caso in cui i due
trasformatori hanno lo stesso rapporto di trasformazione n’=n’’. Inoltre, poiché occorre che sia
n 'V1 − n ''V1 = 0 è necessario che i due morsetti del secondario di ciascun trasformatore sia collegato
in modo che le due tensioni n 'V1 e n ''V1 siano in fase viste dal carico.
'
''
Soddisfatta la condizione a) le due impedenze Z 2e
e Z 2e
risultano collegate in parallelo e una volta
collegato anche il carico il circuito prima considerato diventa:
nV1
Z 2' e
I 2'
Z 2'' e
I 2''
Z
Iz
Questo circuito rappresenta, quindi, la situazione di carico nella quale è richiesto che la corrente I z
si ripartisca nelle sue due componenti secondo lo stesso rapporto delle potenze nominali dei
trasformatori. In termini matematici si ha:
I 2' Pn' V2 I 2' n Z 2' e Vcc'
=
=
=
=
I 2'' Pn'' V2 I 2'' n Z 2'' e Vcc''
Infatti, per il passaggio dalla terza alla quarta eguaglianza è sufficiente considerare il circuito
equivalente semplificato del trasformatore con i parametri riportati al primario per notare che solo
'
''
e Z 2e
sono uguali si ha l’uguaglianza dei moduli delle correnti
se i moduli delle due impedenze Z 2e
nominali. Per il passaggio all’ultima eguaglianza si deve ricordare che la tensione di cortocircuito,
come detto nelle prove dei trasformatori, è proprio la tensione al primario che consente di far
scorrere le correnti nominali.
In definitiva il soddisfacimento della condizione b) richiede che i due trasformatori abbiano le
stesse tensioni di cortocircuito.
Infine, il soddisfacimento della relazione c) impone che le due correnti I 2' e I 2'' siano in fase. Questa
condizione è equivalente a dire che le due correnti devono essere egualmente sfasate rispetto alla
tensione di cortocircuito di ciascuno dei trasformatori, infatti la condizione b) impone che queste
due tensioni siano identiche, e quest’ultima condizione si realizza se le due impedenze Z ' e Z ''
2e
2e
hanno anche lo stesso argomento, ossia se ϕ = ϕ . Questa condizione da un punto di vista pratico
si traduce nel dover assumere che i due trasformatori abbiano lo stesso fattore di potenza di
cortocircuito:
'
cc
''
cc
40
cos ϕcc' = cos ϕcc'' .
Per concludere si mostra brevemente e in modo intuitivo come la richiesta che le due correnti I 2' e
I 2'' siano in fase comporti la riduzione dei loro valori efficaci. A tale scopo è sufficiente analizzare la
costruzione grafica riportata di seguito. Nel primo caso le due correnti I 2' e I 2'' non sono in fase e la
loro somma vettoriale corrisponde alla corrente I z , nel secondo caso si ottiene ancora la corrente
I z con una corrente I 2'' più piccola in modulo rispetto alla precedente, pur mantenendo inalterato il
modulo di I 2' .
Iz
I 2''
I 2'
I 2''
I 2'
Trasformatori trifase
Nei sistemi trifase le tensioni inizialmente rese disponibili dai generatori devono più volte essere
innalzate o abbassate. A tale scopo si possono utilizzare “banchi” di tre trasformatori monofase
distinti e opportunamente collegati.
Se considera, però, la disposizione di tre trasformatori con i nuclei accostati come nella figura
riportata di seguito.
Si intuisce la possibilità di dar luogo ad una struttura ferromagnetica unica tridimensionale a quattro
colonne in cui quella centrale è comune ai tre trasformatori, mentre le altre tre supportano gli
avvolgimenti. La rete magnetica così ottenuta può essere ridotta alla struttura piana della figura
seguente funzionalmente in modo del tutto identico a quella di partenza.
41
Se gli avvolgimenti sono alimentati da una terna simmetrica di tensioni sinusoidali i flussi relativi
alle altre tre colonne sono anche essi sinusoidali e costituiscono una terna simmetrica, ossia si ha:
Φ1 + Φ 2 + Φ 3 = Φ t = 0
La quarta colonna, necessaria per la richiusura delle linee di flusso può, dunque, essere eliminata
alla stessa stregua del quarto filo (neutro) in un sistema trifase simmetrico ed equilibrato, e in
definitiva si può ottenere, la struttura semplificata della figura riportata di seguito, che raffigura un
trasformatore trifase a 3 colonne.
Questa breve discussione fornisce anche le motivazioni che inducono a preferire un trasformatore
trifase a una terna di trasformatori monofase:
a) peso e ingombro ridotti;
b) costi inferiori;
c) manutenzione di una sola unità.
Tuttavia l’utilizzo dei trasformatori trifase comporta anche alcuni svantaggi:
a) peso maggiore della singola unità;
b) costo superiore delle unità di riserva;
c) maggiore onerosità economica delle riparazioni a causa della maggiore complessità della
macchina.
L'impiego di banchi monofase offre, inoltre, il vantaggio esclusivo di garantire una migliore
continuità di esercizio. In caso di guasto su una fase non è necessario sostituire l’intero
trasformatore trifase ma basterà far intervenire una singola unità monofase di riserva.
42
Tipo di avvolgimento
Gli avvolgimenti, distribuiti sul nucleo possono essere collegati, sia al primario che al secondario,
in una molteplicità di modi a seconda delle particolari esigenze operative.
Il tipo di connessione adottato per ciascun gruppo di avvolgimenti ha due importanti conseguenze:
a) il rapporto fra tensioni primarie e secondarie (stellate o concatenate) può essere diverso dal
semplice rapporto spire;
b) le tensioni secondarie non si limitano ad essere in fase o in opposizione rispetto alle
corrispondenti primarie.
In particolare, in relazione al punto b) ogni schema può venire caratterizzato dal cosiddetto gruppo
del trasformatore trifase, definito come la cifra che si ottiene dividendo per 30 l’angolo del quale la
terna delle tensioni stellate del secondario risulta essere in ritardo rispetto a quella del primario.
Gli angoli di sfasamento sono sempre multipli di 30°: anche se i gruppi possibili, almeno in linea di
principio, sono 12, da 0 (terne in fase) a 11 (terna primaria in ritardo di 330°), quelli consigliati dal
C.E.I. sono, però, i gruppi 0 e 6 (tensioni primarie in fase o in opposizione con quelle secondarie) e
i gruppi 11 e 5 (tensioni secondarie in ritardo di 330° o di 150° sulle primarie).
Collegamento triangolo-stella (Dy)
Tra i possibili collegamenti del primario e del secondario si analizza di seguito il caso in cui gli
avvolgimenti di primario sono connessi a triangolo e quelli del secondario a stella indicata
generalmente con le lettere Dy, secondo la convenzione di adottare per il primario le lettere
maiuscole (lato MT) e per il secondario quelle minuscole (lato BT).
Questa è la configurazione classica dei trasformatori utilizzati nel passaggio dalla media alla bassa
tensione nei sistemi di distribuzione dell’energia. Questa scelta è dovuta al fatto il collegamento a
triangolo sul primario tollera meglio i carichi squilibrati e la presenza di componenti armoniche
dovute a forme d’onda non perfettamente sinusoidali. Il collegamento a stella sul secondario,
invece, di fornire due diversi valori di tensione, quello concatenato tra ogni coppia di fasi e quello
stellato (tensione di fase) tra ogni fase e il neutro. Inoltre, il neutro sul lato BT del trasformatore
viene collegato all’impianto di terra nel caso di distribuzione TT o TN.
Il collegamento degli avvolgimenti è quello riportato nella figura di seguito.
T
S
R
+
+
+
Up
Us
0
+
+
+
t
s
r
43
In questo caso dette U p e U s la generica tensione ai capi degli avvolgimenti del primario e del
secondario rispettivamente. Se si fa, inoltre, l'ipotesi di considerare tensioni, correnti e flussi di
induzione perfettamente sinusoidali, trascurando le distorsioni armoniche dovute alla nota non
linearità della caratteristica magnetica del nucleo. Si ha che il modulo della U p coincide con il
modulo delle tensioni concatenate, mentre il modulo della U s coincide con il modulo delle tensioni
di fase, di conseguenza si può determinare il rapporto tra i moduli delle tensioni concatenate dei
sistemi trifase collegati al primario e al secondario del trasformatore. In pratica si ha:
U p = Vp ,
U s = Es ,
Vp
Vs
=
Up
3 Es
=
Up
3U s
=
1
a
=
3 n 3
Per quel che concerne, invece, le fasi di queste grandezze si ha quanto espresso dai diagrammi
fasoriali delle tensioni al primario e al secondario riportati di seguito.
R
r
ER
VRS
Er
0'
0
T
S
Vrs
s
30°
Er
ER
t
Come si vede in figura, la terna delle tensioni stellate secondarie risulta in fase con la terna delle
tensioni concatenate primarie: VRS e Er sono in fase e così, ovviamente accade per le altre tensioni
concatenate e stellate.
Mentre la terna delle tensioni concatenate secondarie è in anticipo di 30° sulle corrispondenti
primarie: Vrs è in anticipo di 30° rispetto a VRS . Come conseguenza, nella stessa relazione di fase
sono le due terne di tensioni stellate.
Lo schema di trasformatore esaminato appartiene, perciò, al Gruppo 11 o al Gruppo 5 (Dy11 oppure
Dy5). Infatti, se la terna di tensioni stellate del secondario risulta in anticipo di 30° rispetto alla
corrispondente terna del primario, essa è anche in ritardo di 330° rispetto a quella del primario e per
la definizione di gruppo si ha: 330°/30=11.
44