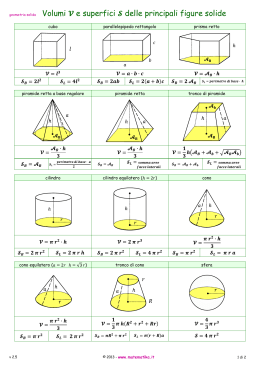
G. Sammito, A. Bernardo,
F. Cimolin, L. Barletta, L. Lussardi
Formulario di matematica
Geometria solida
……………………………………………………………………………………………………………………………………………………………………………
14. GEOMETRIA SOLIDA
Nel seguito: V volume, Al area laterale, Ab area di base, At area totale, 2 pb perimetro di base, C
circonferenza, d diagonale, h altezza, l lato, r raggio, ri raggio della sfera inscritta, rc raggio della sfera
circoscritta, a apotema (in alcuni casi può essere un semplice spigolo).
1. Parallelepipedo rettangono
V = Ab ⋅ c = a ⋅ b ⋅ c
Al = 2 pb ⋅ c
Ab = a ⋅ b
At = 2 Ab + Al = 2 ( ab + bc + ac )
d = a2 + b2 + c2
At − Al V
A
2 pb = l
=
c
2
c
Il baricentro è il punto di intersezione delle diagonali.
Al = At − 2 Ab
Ab =
2. Cubo
V = l3
ri =
l
2
Al = 4l 2
rc =
l
3
2
At = 6l 2
l = 3V =
d =l 3
At
=
6
Al
4
3. Prisma retto
Il prisma retto ha la superficie inferiore congruente e parallela alla superficie
superiore, le facce laterali sono rettangoli.
A
V = Ab ⋅ h
Al = 2 pb ⋅ h
At = Al + 2 Ab
2 pb = l
h
Al
At − Al
V
V
Ab =
Ab =
Al = At − 2 Ab
=
h=
2
h
2 pb Ab
h
4. Prisma obliquo
V = Ab ⋅ h
At = Al + 2 Ab
5. Piramide retta
1
Ab ⋅ h
3
2A
2 pb = l
a
V=
2 pb ⋅ a
2
2 Al
a=
2 pb
Al =
At = Ab + Al
h=
3V
h
3V
Ab
6. Tronco di piramide
1
V = ⋅ h ⋅ ( Ab + Ab′ + Ab ⋅ Ab′ )
3
2 Al
a=
2 p + 2 p′
Ab =
Al =
(2 p + 2 p′) ⋅ a
2
At = Al + Ab + Ab′
…………………………………www.matematicamente.it ………………………………… 1
Formulario di matematica
G. Sammito, A. Bernardo,
F. Cimolin, L. Barletta, L. Lussardi
Geometria solida
……………………………………………………………………………………………………………………………………………………………………………
7. Poliedri regolari
Area e volume si possono calcolare in maniera approssimata utilizzando i numeri fissi φ e σ
A = ϕ ⋅l2
V = σ ⋅ l3
Tetraedro
Esaedro
Ottaedro
Dodecaedro
Icosaedro
Poliedro
o cubo
Numero fisso per
l’area φ
Numero fisso per
il volume σ
1,73
6
3,464
20,64
8,66
0,118
1
0,471
7,663
2,182
Tetraedro: formato da 4 triangoli equilateri
l3 2
l 6
At = l 2 3
V=
ri =
12
12
rc =
l 6
4
l
Esaedro: formato da 6 quadrati è il cubo
l
Ottaedro: formato da 8 triangoli equilateri
l3 2
l 6
V=
ri =
At = 2l 2 3
3
6
Dodecaedro: formato da 12 pentagoni regolari
V=
(
l 3 15 + 7 5
)
(
At = 3l 2 5 5 + 2 5
)
4
Icosaedro: formato da 20 triangoli equilateri
V=
(
5l 3 3 + 5
)
12
At = 5l 2 3
l
h
tetraedro
rc =
ri =
ri =
l
l 2
2
(
l 10 25 + 11 5
)
20
(
l 3 3+ 5
)
rc =
rc =
12
(
l 3 1+ 5
)
4
(
l
2 5+ 5
4
)
8. Cilindro
V = Ab ⋅ h = πr 2 h
Ab = πr 2
At = Al + 2 Ab = 2π r (h + r )
C = 2π r =
Al
h
h=
Al
V
= 2
2π r π r
Al = C ⋅ h = 2πrh
V
Ab =
h
A
V
r= l =
2π h
πh
9. Cono
V=
Ab ⋅ h π ⋅ r 2 ⋅ h
=
3
3
At = Ab + Al = πr 2 + πra
C ⋅a
= πra
Ab = πr 2
2
A
A
3V
r= l =
a= l
πa
πh
πr
Al =
h=
3 ⋅V
π r2
…………………………………www.matematicamente.it ………………………………… 2
Formulario di matematica
G. Sammito, A. Bernardo,
F. Cimolin, L. Barletta, L. Lussardi
Geometria solida
……………………………………………………………………………………………………………………………………………………………………………
10. Tronco di cono
1
V = hπ ( r12 + r1r2 + r22 )
3
a = h 2 + ( r1 − r2 )
Al = π ⋅ a ⋅ (r1 + r2 )
Ab = πr12 + πr22
2
11. Sfera
4
V = πr 3
3
A = 4πr 2
r=
A 3 3V
=
4π
4π
Calotta sferica e segmento sferico
ad una base o sezione sferica
1
V = πh 2 (3r − h)
A = 2πrh
3
r1 = h ( 2r − h )
h
Settore sferico
Al = π r ( r1 + 2h )
2
V = π r 2h
3
r1
h
r1
r
r
Zona sferica e segmento sferico a due basi
⎞
π ⋅ h ⎛ h2
V =
⋅ ⎜⎜ + r12 + r22 ⎟⎟
A = 2πrh
2 ⎝ 3
⎠
Fuso sferico e spicchio sferico
π r3
π r2
V=
α
α,
Al =
270°
90°
α è misurato in gradi
Al è la parte di
superficie sferica
α
r
12. Altre figure particolari
Cilidro circolare retto a sezione obliqua
(a + b)
V = π r2
Al = π r ( a + b )
2
2
⎛
⎛ a − b ⎞ ⎟⎞
At = π r ⎜ a + b + r + r 2 + ⎜
⎟
⎜
2 ⎠ ⎟
⎝
⎝
⎠
Corona cilindrica
V = π h ( r12 − r22 )
Al = 2π h ( r1 + r2 )
At = 2π ( r1 + r2 )( h + r1 − r2 )
r1
a
r
b
r2
…………………………………www.matematicamente.it ………………………………… 3
Formulario di matematica
G. Sammito, A. Bernardo,
F. Cimolin, L. Barletta, L. Lussardi
Geometria solida
……………………………………………………………………………………………………………………………………………………………………………
Obelisco
Le superfici laterali sono trapezi, le superfici
superiore e inferiore sono rettangoli non simili.
h
V = ⎡⎣( 2a + c ) b + ( 2c + a ) d ⎤⎦
6
c
Cuneo
Superficie di base rettangolare, le superfici laterali
sono triangoli e trapezi isosceli.
bh
V = ( 2a + c )
6
c
d
h
h
b
b
a
a
Toro
V = 2π r r
2 2
2 1
r1
At = 4π r1r2
2
r2
Prisma obliquo triangolare
a+b+c
V = Ab
3
a
b
c
Ab
…………………………………www.matematicamente.it ………………………………… 4