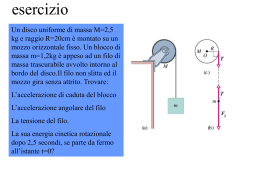
Problemi: dinamica
1. Un blocco di massa M = 3.3 kg scorre su una superficie orizzontale senza
attrito. Tale blocco è legato mediante una fune che passa attraverso una
puleggia ad un secondo blocco di massa m = 2.1 kg.
Fune e puleggia sono prive di massa. Mentre il blocco appeso cade, il
blocco scorrevole subisce una accelerazione verso destra. Si calcoli:
a) accelerazione del blocco M;
b) accelerazione del blocco m;
c) tensione della corda.
blocco M:
Fnet , x = Ma x = T = Ma
Fnet , y = Ma y = N − Mg = 0
blocco m:
Fnet , x = ma x = 0
Fnet , y = ma y = T − mg = −ma
i due corpi hanno stressa accelerazione
T = Ma
T − mg = −ma
⇒
a !!!
Ma = −ma + mg
a=
m
2.1 kg
g=
9.8m / s 2 = 3.8 m / s 2
m+M
(3.3 + 2.1) kg
T=
Mm
(3.3kg )(2.1 kg )
g=
9.8m / s 2 = 13 N
m+M
(3.3 + 2.1) kg
attenzione a
decimali e
cifre significative !!
2. Un blocco di massa M = 15.0 kg è sospeso mediante 3 corde legate ad
un nodo di massa mK , disposte come nel disegno. Le corde hanno massa
trascurabile e si può ignorare la forza di gravità sul nodo.
Quali sono i moduli delle tensioni nelle 3 corde ?
blocco
T3 − Mg = Ma y = 0
T3 = Mg = (15.0 kg )(9.8m / s 2 ) = 147 N
3 cifre significative
nodo
r r r
r
T1 + T2 + T3 = mK aK = 0
T1x + T2 x + T3 x = 0

T1 y + T2 y + T3 y = 0
− T1 cos 280 + T2 cos 47 0 + 0 = 0

 T1 sin 280 + T2 sin 47 0 − T3 = 0
− 0.88 T1 + 0.68 T2 = 0


0.47 T1 + 0.73 T2 − 147 N = 0
 T1 = 103.9 N = 104 N

T2 = 134.5 N = 134 N
[N.B. devo avere al massimo 3 cifre significative!]
3. Un blocco di massa m = 15 kg è trattenuto da una fune su un piano liscio
inclinato di un angolo θ=270.
a) determinare la tensione T e la forza N;
b) se ora taglio la fune, quanto vale l’accelerazione del blocco?
r r r
r
T + N + Fg = ma = 0
a)
decompongo in x e y:
T + 0 − mg sin θ = 0
0 + N − mg cos θ = 0
T = (15kg )(9.8m / s 2 ) sin 27 0 = 67 N
N = (15kg )(9.8m / s 2 ) cos 27 0 = 131N
b)
elimino la tensione T:
 Fgx = ma x

 Fgy = N
⇒
− mg sin θ = ma
a = − g sin θ = −(9.8m / s 2 ) sin 27 0 = −4.4m / s 2
N.B. il modulo di a è inferiore a g essendo dovuta
solo alla componente di Fg lungo il piano.
4. Un passeggero di massa m = 72.2 kg sta su una bilancia nella cabina di
un ascensore.
a) Trovare una soluzione generale per la lettura della bilancia,
valida per qualunque moto verticale della cabina.
b) che valori leggo sulla bilancia se l’ascensore è fermo o si muove
con moto uniforme di velocità v = 0.50 m/s ?
c) che valori leggo se l’ascensore risente di una accelerazione verso l’alto
o verso il basso pari ad a = 3.20 m/s2 ?
d) durante l’accelerazione verso l’alto quale è il modulo della forza netta
sul passeggero e qual è l’accelerazione impressa al passeggero dal punto
di vista del sistema di riferimento in moto? Il loro rapporto è m?
r r
r
a) N + Fg = ma
N − Fg = ma
N = m( g + a )
la lettura della bilancia
dipende da a
b) ar = 0
N = mg = (72.2 kg )(9.8m / s 2 ) = 708 N
r
c) a = 3.20m / s 2
N = m( g ± a )
939 N
= (72.2 kg )(9.8m / s 2 ± 3.20m / s 2 ) = 
477 N
r
r r
d) Fnet = N + Fg = mar
Fnet = N − Fg = m( g + a ) − mg = ma = 231N
accelerazione del passeggero rispetto a cabina è 0
⇒ F/a ≠ m NON vale la legge di Newton (sistema non inerziale)
Problemi: forze di attrito e ritardanti
5. Se le ruote di un’auto sono bloccate durante una frenata di emergenza
l’auto slitta sulla strada. Le tracce di frenata più lunghe (290 m) sono state
misurate nel 1960 in Gran Bretagna. Supponendo che il coefficiente di
attrito dinamico fosse µd = 0.60, calcolare la velocità dell’auto all’istante
di bloccaggio delle ruote.
L’accelerazione è costante
[le ruote sono bloccate]
applico le leggi del moto ad
accelerazione costante
v 2 = v02 + 2a ( x − x0 )
(1)
v=0
x − x0 = 290 m
devo determinare a [è una decelerazione]
L’unica forza idonea a provocare a è la forza di attrito:
Fnet ,a = ma x
f d = µd N
− f d = ma x
N = mg
Sostituendo in (1):
µ mg
fd
=− d
= − µ d g = −0.60 ⋅ 9.8m / s 2 = −5.9 m / s 2
m
m
v0 = 2 µ d g ( x − x0 )
a=−
= 2(0.60 )(9.8m / s 2 )( 290 m )
58 ⋅10 − 3
= 58 m / s =
km / h = 209 km / h
1 / 3600
6. Una donna tira a velocità costante una slitta carica di massa m=75 kg,
su una superficie orizzontale. Il coefficiente di attrito dinamico fra
i pattini e la neve è µd=0.10, e l’angolo φ è di 420.
a) qual è il modulo T della tensione della fune?
b) se la donna tira la fune in modo che T aumenti,
il modulo della forza di attrito aumenta, diminuisce o rimane uguale ?
a) Idea chiave: v è costante ⇒ a = 0
malgrado la slitta sia sotto tiro
la sua accelerazione è nulla !!
r
r r r
r
T + N + Fg + f d = ma = 0
decompongo in x ed y:
Tx + 0 + 0 − f d = 0

 Ty + N − Fg = 0
 T cos φ − µ d N = 0

T sin φ + N − mg = 0
ho un sistema di 2 equazioni nelle 2 incognite T ed N:
T cos φ
N=
µd
T cos φ
mg −
mg − N
µd
T=
=
sin φ
sin φ
T sin φ = mg −
T cos φ
µd
T ( µ d sin φ + cos φ ) = µ d mg
T=
(0.10)(75kg )(9.8m / s 2 )
µ d mg
=
= 91 N
µ d sin φ + cos φ (0.10)(sin 420 ) + cos 420
b) La forza di attrito è proporzionale ad N, quindi vedo come cambia N con T.
Uso l’equazione in y:
N = mg − T sin φ ⇒ al crescere ti T, N diminuisce.
[aumenta la componente di T verso l’alto che quindi
riduce la forza normale applicata dalla neve sulla slitta]
7. Una piccola sfera di massa m=3.00 g è rilasciata dalla quiete
a t = 0 in una bottiglietta di shampoo liquido. Sapendo che la
velocità limite è vT=2.00 cm/s, trovare:
a) il valore della costante b;
b) il tempo τ necessario per raggiungere 0.632 vl,
c) il valore della forza ritardante quando la sferetta raggiunge
la velocità limite
8. Una goccia di pioggia di raggio R=1.5 mm cade da una nuvola
che si trova ad altezza h = 1200 m sopra il terreno.
Il coefficiente aerodinamico D per la goccia vale 0.60.
Supponendo la goccia sferica ed assumendo per le densità
di aria e acqua i valori ρa = 1.2 kg/m3 ed ρw=1000 kg/m3
a) quale è la velocità limite della goccia ?
b) quale sarebbe la velocità raggiunta appena prima dell’impatto
con il terreno se non vi fosse alcuna forza di resistenza del mezzo ?
a)
idea chiave: la velocità limite viene raggiunta quando
la forza di gravità
bilancia la resistenza aerodinamica del mezzo
1
2
Fg = R = DρAvl
2
4
Fg = mg = ρ wVg = ρ w g ( πR 3 )
3
vl =
2 ρ w g 4πR 3
8 Rgρ w
=
=
Dρ a A
3Dρ aπR 2
3Dρ a
2 Fg
8(1.5 ⋅10 −3 m)(9.8m / s 2 )(1000kg / m 3 )
=
3(0.60)(1.2kg / m 3 )
7.410 −3 km
= 7.4 m / s =
= 27 km / h
1 / 3600h
b) idea chiave: senza la resistenza dell’aria la goccia risente della
accelerazione g [moto uniformemente accelerato]
v 2f = v02 + 2 g ( x f − xi ) = v02 + 2 gh
v f = 2 gh = 2(9.8m / s 2 )(1200m)
= 153 m / s ≈ 550 km / h
Problemi: forza centripeta/ moto circolare
9. Un oggetto di massa m1 percorre una
circonferenza di raggio R su un piano
R
privo di attrito, e sostiene un corpo
m1
di massa m2 sospeso ad un filo che passa
attraverso un foro al centro della circonferenza.
Se l’oggetto sospeso rimane in equilibrio,
m2
a) quale è la tensione della fune ?
b) quale è la forza risultante sul disco ?
c) quale è la velocità del disco ?
diagrammi delle forze:
r
T
r
Fg
m2
r r
T = Fc
m1
10. Un’automobile di massa m=1600 kg viaggia con velocità
costante su una pista circolare di raggio R = 190 m.
Quale è il valore minimo del coefficiente di attrito µs
(pneumatici-terreno) che impedisce alla macchina di slittare
verso l’esterno ?
idee chiave:
1) se l’auto percorre traiettoria
circolare è sottoposta a forza centripeta
2) unica forza orizzontale che agisce su
auto è attrito
⇒ forza centripeta = attrito
3) l’auto non slitta verso l’esterno
quindi è un attrito statico
4) se l’auto è sul punto di slittare il modulo della
forza di attrito è massimo
f s ,max
f s ,max
mv 2
=
R
= µs N
⇒
mv 2
= µs N
R
mv 2 mv 2
(20m / s ) 2
µs =
=
=
= 0.21
NR mgR (9.8m / s 2 )(190m)
se µs < 0.21 l’auto slitta
verso l’esterno
N.B. 4 µs ∝ v2 [ho bisogno di attrito maggiore
per mantenere auto veloce in curva]
4 µs non dipende da m [vale per ogni corpo]
11. Un ingegnere vuole progettare una rampa sopraelevata
per la strada, tale che le macchine non debbano fare
affidamento sull’attrito per affrontare la curva senza
slittare. Si supponga che l’auto percorra la curva a
48 km/h e che il raggio della curva sia 50.0 m.
Con quale angolazione deve essere sopraelevata
la curva ?
Idea chiave: la forza centripeta è data dalla forza di attrito
macchina-strada
12. Nel rotore del Luna Park una persona viene fatta ruotare
molto velocemente dentro un cilindro. La persona
rimane bloccata contro la parete quando il pavimento
del cilindro viene aperto.
Il coefficiente di attrito statico tra la persona e la parete
è µs ed il raggio del cilindro è R.
a) determinare il massimo periodo
di rotazione necessario perché
la persona non cada.
b) dare un valore numerico per
T se R=4.00m e µs =0.400.
Quanti giri al minuto deve
compiere il cilindro?
13. Un satellite geostazionario (o sincrono) orbita attorno alla Terra
seguendo un’orbita perfettamente sferica e con un periodo orbitale
coincidente con il periodo di rotazione della Terra attorno al
proprio asse. Si calcolino:
a) la quota del satellite rispetto al centro della Terra;
b) la sua velocità orbitale.
Idea chiave:
la forza centripeta che mantiene
il satellite in orbita è data dalla
forza di gravità Terra-satellite.

M T msat msat v 2
=
 Fg = G
2
r
r

 v = ωr = 2π r

T
MeteoSat
2
msat v 2 msat  2π 
4π 2
=
r  = 2 msat r

r
r  T 
T
M T msat 4π 2
G
= 2 msat r
r2
T
GM T T 2 = 4π 2 r 3
2
2
2
24
2
−11
GM
T
×
Nm
kg
×
×
×
(
6
.
6
10
/
)(
5.98
10
kg)(24
60
60s)
T
r =3
=3
2
4π
4π 2
= 4.225 ×106 m ≈ 42250 km
Sapendo che il raggio della terra è RT≈6370 km la quota del
satellite, sopra la superficie terrestre è
h = r − RT ≅ 35880 km
Ricavo la velocità orbitale del satellite:
M T msat msat v 2
G
=
r2
r
MT
(6.6 ×10 −11 Nm 2 / kg 2 )(5.98 ×10 24 kg)
v= G
=
≈ 3070m / s ≈ 3km / s
r
4.23 ×107 m
N.B. r e v NON dipendono dalla massa del satellite !!!