L’esperimento di Haynes e Shockley
Introduzione
L'esperimento proposto nel 1949 da J.R.Haynes e W.Shockley 1 per misurare la mobilità
di deriva di elettroni e lacune nei semiconduttori è estremamente semplice dal punto di
vista concettuale anche se presenta alcune difficoltà nella preparazione dei campioni,
nell'uso dei contatti a punta e nella rivelazione del segnale. Si tratta di un esperimento di
grande valore didattico perchè consente una visualizzazione diretta dei fenomeni di
deriva, diffusione e ricombinazione dei portatori in eccesso. Nella versione qui usata si
utilizza un sistema di iniezione ottica dei portatori in eccesso, che elimina la difficoltà
di un buon contatto iniettante.
1. L'esperimento originale di Haynes e Shockley.
L'esperimento di H S si basa su questo principio: in una sbarretta di semiconduttore
monocristallino drogato, viene creato un campo elettrico da un'estremità all'altra.
Successivamente viene inviato in un punto del campione un breve impulso di portatori
minoritari di carica, i quali vengono trasportati dal campo suddetto lungo la sbarra.
Se ne riveliamo il passaggio in un punto "a valle" della zona di emissione (prima che
essi si ricombinino e prima che il numero di urti da loro subìto diventi tale da
1
J.R.Haynes e W.Shockley, Phys.Rev. 75,691 (1949) e Phys.Rev. 81,835 (1951); A.Sconza and
G.Torzo Eur.J.Phys.8, 34-40 (1987); A. Sconza, G. Galet and G. Torzo Am. J. Phys, 68, 8087 (2000)
1
disperderli), studiando le caratteristiche dell'impulso letto, potremo trarre notizie su
velocità di deriva, vita media e coefficiente di diffusione del cristallo.
Figura 1: Schema dell’apparato originale di H-S
Lo schema originale dell’esperimento di Haynes e Shockely è rappresentato in figura 1.
Consideriamo una sbarretta di semiconduttore drogato P, lunga l (alcuni centimetri),
con due contatti ohmici saldati alle estremità.
All'interno del cristallo si produce un campo elettrico Es, detto campo di spazzolamento
(Es≤10V/cm), mediante un generatore di tensione pulsato schematizzato nella figura 1
come una batteria più un interruttore.
Due contatti a punta (elettrodi E e C) vengono appoggiati alla superficie del cristallo,
separati da una distanza d di alcuni millimetri. I contatti a punta sono (almeno
parzialmente) rettificanti e perciò vengono rappresentati come diodi.
Se si applica all'elettrodo E (emettitore) un impulso negativo di pochi microsecondi di
durata e di ampiezza sufficiente a polarizzare direttamente il diodo DE, si avrà iniezione
di elettroni nella regione del cristallo immediatamente sottostante alla punta E. Questo
fiotto di elettroni, sotto l'azione del campo di spazzolamento Es, comincerà a spostarsi
verso destra con velocità di deriva vd, e dopo un certo tempo t raggiungerà la zona del
cristallo sottostante alla punta C (collettore).
Questo secondo diodo DC è polarizzato inversamente (infatti il suo "catodo" è collegato
verso massa tramite la resistenza R ed il suo "anodo" è a contatto col cristallo che è
tutto a potenziale negativo) e quindi attraverso la resistenza R fluisce solo la debole
corrente inversa del diodo (elettroni dal semiconduttore P al metallo). L'arrivo del fiotto
di elettroni, aumentando la concentrazione dei portatori minoritari nella regione del
contatto C, provoca un aumento della corrente inversa e quindi un abbassamento del
potenziale all'estremo della resistenza connessa al collettore.
Sullo schermo dell'oscilloscopio, connesso ai capi della resistenza R, si osserva un
primo impulso negativo stretto e di ampiezza confrontabile con quella dell'impulso di
2
iniezione e, con un certo ritardo t, un secondo impulso negativo più largo e di ampiezza
minore.
Figura 2: Esempio di segnali ottenuti in Ge-N con iniezione a punta
Il primo picco è contemporaneo all'impulso di iniezione: esso è infatti il segnale di
propagazione del campo elettromagnetico che viaggia nel cristallo come in ogni
conduttore, alla velocità della luce (entro quel mezzo). Il secondo impulso invece
corrisponde al passaggio sotto il collettore del fiotto di elettroni: la sua forma
approssimativamente gaussiana e la sua ampiezza sono determinate dai fenomeni di
diffusione e ricombinazione.
Una interpretazione analitica della forma dell’impulso raccolto basata sulla soluzione
dell'equazione della diffusione dipendente dal tempo, si può trovare in letteratura (rif.
1). Tale descrizione procede lungo le linee seguenti.
Immediatamente dopo l'iniezione degli elettroni in eccesso, entro un tempo dell'ordine
di ε/σ (dielectric relaxation time dell'ordine dei 10-12 s tipicamente, ε=costante
dielettrica, σ=conducibilità), una concentrazione di lacune in eccesso neutralizza la
concentrazione degli elettroni in eccesso nella zona di iniezione. L'aumento della
densità di portatori riduce la resistenza del campione e provoca quindi una immediata
variazione del potenziale della punta C (di segno negativo e durata pari alla durata
dell'iniezione).
Successivamente gli elettroni in eccesso si muovono assieme alle lacune in eccesso
μ μ (p − n)
dalla punta E alla punta C con una mobilità effettiva μ* = e h
che, dal
μe n + μh p
momento che il cristallo è drogato P (p>>n), si riduce a μ*≈μe cioè alla mobilità dei
portatori minoritari (elettroni). Quando questa "nuvola" di portatori in eccesso
raggiunge il collettore C questo raccoglie i portatori minoritari e quindi ai capi di R si
produce un segnale negativo di forma (approssimativamente) gaussiana.
3
L’impulso raccolto ha una forma ed un’area che dipendono dal tempo, dalla distanza
percorsa (d) e dalla velocità di deriva.
Gli elettroni iniettati, infatti, man mano che derivano verso il collettore, diffondono in
tutte le direzioni per cui l'impulso rivelato si allarga sempre più al crescere del ritardo t.
Gli elettroni inoltre si ricombinano con le lacune che incontrano lungo il percorso, per
cui il numero di elettroni che raggiungono effettivamente il collettore decresce
esponenzialmente nel tempo secondo la legge:
N(t) = No exp (-t/τ)
[1]
dove τ è la vita media di ricombinazione dei portatori in eccesso.
La misura del ritardo t (tempo di volo) e della distanza d fra le punte fornisce la velocità
di deriva vd degli elettroni:
vd = d/t
[2].
2. Informazioni che si possono estrarre dalla misura dell’impulso raccolto.
Dalla misura dell'ampiezza VS dell'impulso di spazzolamento e della lunghezza l del
cristallo si ottiene il valore del campo di spazzolamento ES =VS/l e quindi della
mobilità μ degli elettroni
μ = |vd|/|ES| = d l / (t VS)
[3].
Dalla misura della larghezza a metà altezza Δt dell'impulso di collettore corrispondente
al passaggio dei portatori iniettati, si può ricavare il valore della costante di diffusione
D, mediante la relazione:
[4]
(vd Δt)2 = 11.08 D t
(valida se la durata dell'impulso di iniezione è trascurabile rispetto al ritardo t e alla
larghezza Δt). Infatti, come spiegato in Appendice 2, la diffusione determina uno
"sparpagliamento" gaussiano dei portatori iniettati. Questa distribuzione gaussiana di
larghezza a metà altezza Δx= 11.08Dt per effetto del campo di spazzolamento
"scorre" lungo il cristallo con una velocità di deriva vd e quindi impiega il tempo
Δt=Δx/vd a passare sotto il collettore .
Il rapporto D/μ obbedisce alla relazione di Einstein: D/μ=kT/e, (dove k è la costante
di Boltzmann, T la temperatura assoluta ed e la carica elementare) che a 300K dà
D/μ=0.026 Volt.
Dalle relazioni (4) e (2) si può ottenere una formula per calcolare direttamente D/μ:
basta sostituire vd2 con (d/t μES) e si ha:
VS d
D/μ =
(Δt/t)2
(5)
11.08 l
4
Dalla misura dell'area A racchiusa dall'impulso di collettore si può ottenere almeno
una stima della vita media τ dei portatori in eccesso; si ha infatti
∞
∞
0
0
∫
A = Vc (t ')dt ' = R Δi(t ')dt ' ∝R e η N,
∫
dove Δi(t’) = VC(t’)/R è l'aumento della corrente inversa del collettore quando viene
raggiunto dall’impulso, VC(t’) l'ampiezza dell'impulso, η l'efficienza con cui il
collettore raccoglie i portatori minoritari, e la carica elementare ed N il numero di
portatori iniettati che transitano sotto il collettore.
Poiché N diminuisce col tempo t secondo la relazione [1] si ha appunto:
A(t) = Aoexp(-t/τ)
[5].
Le stesse informazioni si possono ottenere per le lacune, usando un cristallo drogato N,
ed impulsi di spazzolamento e di iniezione positivi anziché negativi. La polarità dei
diodi equivalenti ai contatti a punta sarà rovesciata rispetto a quella di figura 1.
3. L’apparato con iniezione mediante effetto fotoelettrico.
E’ anche possibile creare i portatori in eccesso mediante un impulso di luce (sfruttando
l’effetto fotoelettrico interno), ad esempio usando luce prodotta da un diodo LASER e
immessa in una fibra ottica la cui estremità libera viene affacciata al cristallo di Ge al
posto della punta E.
Questo semplifica l'esecuzione dell'esperimento: si usa un solo contatto a punta
(collettore) evitando di dover aggiustare la tensione dell’impulso di iniezione (in
funzione della posizione del contatto emettitore sul cristallo ed in funzione della
tensione di spazzolamento) 2 , e si riesce a creare una maggior quantità di portatori in
eccesso in un tempo più breve (la durata dell'impulso di luce è regolabile tra 20 e 200
ns), con una miglior definizione del tempo di volo.
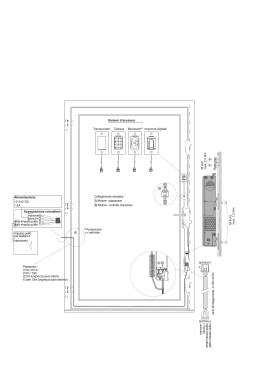
L’apparato (schematizzato in figura 3) è costituito da :
a) Campione semiconduttore a barra con due contatti ohmici alle estremità
b) Porta-campione con slitta per fibra ottica e slitta per contatto a punta ("collettore")
c) Impulsatore doppio per dare l'impulso di spazzolamento e l'impulso di luce con
amplificatore differenziale per sottrarre il segnale di spazzolamento
2
Come spiegato in dettaglio in A. Sconza, G. Galet and G. Torzo Am. J. Phys, 68, 80-87 (2000)
5
E’ inoltre necessario utilizzare un oscilloscopio: particolarmente efficace è l’uso di un
oscilloscopio digitale con capacità di mediare molti impulsi con banda passante di
almeno 60 MHz ed interfaccia per memorizzare la forma dell’impulso.
Figura 3: Schema a blocchi di apparato con iniezione ottica e collettore a punta
3.1. Il campione
Il campione semiconduttore è una sbarretta (all’incirca 4x4x30 mm) tagliata da un
monocristallo semiconduttore, con contatti ohmici alle due estremità. Conviene usare il
Ge perché i contatti terminali si realizzano facilmente a stagno. La preparazione dei
campioni di Ge richiede di levigare ("lappare") il cristallo su una superficie piana con
una carta abrasiva finissima (n.2000) e acqua fino a fargli assumere un aspetto
speculare e quindi lucidarlo con pasta diamantata, successivamente il cristallo va
immerso in CP4 3 per circa 1 minuto in modo da pulire chimicamente la superficie, e
quindi lavato in acqua distillata. A questo punto i due fili terminali si saldano a stagno
senza problemi (eventualmente con una goccia di disossidante Castolin).
Il Ge è un materiale molto costoso ed una sbarretta delle dimensioni indicate ha un
prezzo dell'ordine di circa 200 € (converrebbe usare il Si il cui costo è inferiore di un
ordine di grandezza, ma su cui è molto più difficile fare i contatti ohmici 4 ).
3
Il CP4 è una miscela di acido nitrico (60%), acido acetico (30%) ed acido fluoridrico (10%). E’ una
sostanza tossica, da usare con molta cautela evitando il contatto con la pelle e l'inalazione dei vapori.
4 Occorre infatti depositare sotto vuoto uno strato di Al (su Silicio P) o di Au (su Silicio N) alle estremità
della sbarretta, far diffondere il metallo entro il Si con un opportuno riscaldamento in atmosfera inerte ed
infine incollare i fili terminali mediante una resina conduttrice a base di argento (Silverpaint).
6
3.2. Il porta-campione con slitte scorrevoli per contatto a punta e fibra ottica
Il cristallo è fissato su un supporto isolante ed allineato con l’asse delle due slitte che
portano il contatto a punta e la fibra ottica.
Figura 4: Portacampione con slitte per fibra e punta
La fibra ottica (diametro 200 μm) è otticamente accoppiata al diodo laser e bloccata alla
slitta in posizione verticale a circa un millimetro dalla superficie del campione. E’
importante che la fibra sia centrata sul campione, e verticale rispetto ad esso, perché le
coppie prodotte in prossimità delle facce laterali si ricombinano rapidamente per effetto
dei difetti superficiali che agiscono da centri di ricombinazione.
Come punta si può usare un ago di acciaio da ricamo montato su supporto elastico,
oppure un aguzzo puntale a molla saldato su una basetta per circuiti stampati. E’
importante che si possa variare comodamente la posizione del contatto a punta per
trovare una regione del cristallo ove il coefficiente di raccolta sia elevato (questo
dipende dallo stato della superficie del campione).
3.3. L’impulsatore
Il campo di spazzolamento non può essere applicato costantemente al cristallo se si
vuole evitare di surriscaldarlo. Occorre quindi un generatore di impulsi di tensione con
ampiezza regolabile (fino a Vmax≈50V), di durata dell'ordine di alcune centinaia di
microsecondi e con frequenza di ripetizione tra 30 e 50 Hz 5 .
5
Il rapporto tra la potenza dissipata con una tensione di spazzolamento impulsata e quella dissipata con
polarizzazione in d.c. è pari al rapporto tra tempo di accensione t1 e tempo di spegnimento t2 (duty cicle)
e per impulsi brevi è ben approssimato dal prodotto t1×f (ove f è la frequenza di ripetizione).
7
Occorre poi un secondo impulsatore sincronizzato con il primo per produrre l'impulso
di accensione del LASER (iniezione di coppie elettrone-lacuna).
L'impulso di iniezione deve essere prodotto con un certo ritardo rispetto all'inizio
dell'impulso di spazzolamento in modo che i fenomeni transitori di modulazione della
conduttività elettrica del cristallo, dovuti ad una non perfetta ohmicità dei contatti
terminali, abbiano modo di esaurirsi prima della iniezione degli elettroni.
Per l'esperimento con cristalli di tipo N servono impulsi positivi mentre per i cristalli di
tipo P servono analoghi impulsi negativi. Per questo motivo si utilizza un alimentatore
di tensione con uscite “floating” (che possono cioè essere collegate alternativamente a
massa, per fornire l'impulsi di spazzolamento VS positivi o negativi) connesso al
campione tramite un interruttore elettronico. La polarità desiderata viene selezionata da
un deviatore a pannello.
3.3.1. Il generatore dell’impulso di spazzolamento
Il generatore dell’impulso di spazzolamento è ricavato da un Timer NE555, nella
configurazione free running (figura 5), che produce la temporizzazione(CLOCK),
seguito da un divisore 26. Il periodo di clock è dato dalla relazione T=ln2(R1+2R2)C.
Figura 5: Schema del Timer 555 configurato come multivibratore astabile
Il divisore è un 12-stage binary ripple counter CD4040 (figura 6), seguito da due porte
NAND (CD4082) che determinano il duty cycle dell’impulso di spazzolamento.
8
Il CD4082 è costituito da una serie di 12 FLIP-FLOP (uscite Qi) ciascuno dei quali
divide la frequenza di ingresso per 2 : quindi l’uscita Q0 ha frequenza f/2, l’uscita Q1
f/4, Q2 f/8 , Q3 f/16, Q4 f/32 e infine l’uscita Q5 è una onda quadra a frequenza f/64,
ovvero con periodo pari a 64 T.
La prima porta NAND a quattro ingressi (Q5-Q8) commuta ogni 24=16 periodi della
frequenza dell’uscita di Q5, e la seconda porta (sfruttando le uscite Q9 e Q10) commuta
ogni 26=64 periodi di Q5.
Tuttavia la durata dell’impulso positivo τs all’uscita della seconda porta, è uguale alla
durata dell’impulso positivo più breve tra tutti quelli dei segnali utilizzati agli ingressi
delle due porte, cioè la durata delll’impulso all’uscita Q5 (τs = 64 T), mentre resta a
tensione zero per tutto il tempo che serve a completare un periodo del segnale alla
frequenza più bassa (Q10).
Questo è il segnale VSL( ad ampiezza fissa) che comanda lo spazzolamento.
Quindi il tempo di spegnimento che segue l’impulso di polarizzazione del campione è
sempre 64 volte la durata dell’impulso.
La durata τs dell’impulso di spazzolamento, è regolata mediante il potenziometro P1
(R2 nello schema di figura 5) che varia il periodo T del multivibratore.
La durata dell’impulso di spazzolamento varia nell’intervallo 300-500 μs.
Figura 6: Divisore per 64 e formatore di impulso VSL
Il segnale di potenza VS per polarizzare il cristallo con la tensione di spazzolamento è
ottenuto accendendo (mediante foto-accoppiatore ottico per disaccoppiare i riferimenti
di massa) un interruttore a MOSFET che applica ai contatti ohmici alle estremità del
cristallo la tensione prodotta da un generatore con massa fluttuante (figura 7).
9
L’ampiezza della tensione di spazzolamento (tra 5 e 50V) è scelta tramite il
potenziometro P3 che controlla il regolatore di tensione TL783. La polarità
dell’impulso è scelta mediante il doppio deviatore SW2: nella posizione N (per cristalli
drogati N ove serve impulso positivo per osservare il moto delle lacune, portatori
minoritari) viene messa a massa comune la polarità negativa del generatore di tensione,
per cristalli drogati P viene invece messa a massa la polarità positiva, e si ottiene un
impulso negativo per osservare la deriva degli elettroni.
Figura 7: Schema semplificato (sopra) e a blocchi (sotto) del generatore di segnale Vs
La potenza W dissipata nel cristallo si calcola facilmente conoscendo la resistenza R del
campione tramite la relazione : W=(Vs)2/64R.
3.3.2. Il generatore dell’impulso per il diodo laser
Una linea di ritardo regolabile tramite il potenziometro P2 (figura 6), che varia la
costante di tempo RC all’ingresso di un monostabile (CD4538), fornisce il ritardo con
cui è dato il segnale di innesco (fronte di salita all’uscita Q negata) al circuito pilota per
l'accensione del diodo LASER (segnale LASERTRIG).
L’impulso all’uscita Q del monostabile è disponibile ad una boccola BNC sul pannello
frontale . Questo segnale ha il fronte di salita all’inizio dell’impulso di spazzolamento e
il fronte di discesa all’inizio dell’impulso LASER: in tal modo il trigger
dell’oscilloscopio può essere facilmente sincronizzato con l’inizio dello spazzolamento
o con l’inizio della iniezione di fotoni se si usa questo segnale come external trigger,
semplicemente scegliendo il fronte di salita o di discesa in modalità edge trigger ).
Il formatore di impulsi per il diodo LASER è schematizzato in figura 8.
10
Figura 8: Circuito formatore dell’impulso laser
Il segnale LASERTRIG, comanda la prima porta del Quad-NAND 74HC132, se essa
non è inibita dall’interruttore SW1 che pone a massa l’altro ingresso (comando di
ON/OFF dell’impulso di luce). All’uscita il segnale invertito viene derivato da un filtro
C-R. Lo spike risultante viene squadrato e di nuovo invertito dal secondo NAND.
L’impulso risultante (largo circa 2 µs) viene inviato ai due ingressi del terzo NAND,
direttamente ad una porta e tramite un filtro RC ed un inverter (74HC14) all’altra porta.
Gli ingressi del terzo NAND si trovano allo stesso livello da quando è arrivato
l’impulso prodotto dal secondo NAND solo per un intervallo di tempo pari al ritardo
τ=RC << 2 µs (regolabile tramite il potenziometro P4). All’uscita del terzo NAND
compare un impulso negativo di durata τ. Questo impulso viene usato per pilotare in
parallelo 4 moduli di potenza (costituiti ciascuno da un MOSFET TN0106A) abilitati o
disabilitati da altrettante porte NAND di potenza (74F3037).
Il parallelo di questi interruttori veloci è reso necessario dalla elevata corrente di picco
richiesta dal diodo LASER (circa 6 A per il modello C86150E della EG&G). La
corrente viene erogata da un banco di condensatori tra loro in parallelo alimentati dal
generatore fluttuante da 30V tramite un regolatore di tensione (LM317) ed il
potenziometro P5 che consente di variare la tensione di carica dei condensatori e quindi
la corrente totale che attraversa il diodo LASER in ogni impulso (e in definitiva il
numero di fotoni emessi).
Specifiche del diodo LASER C86150E (P/N PGAS1S09):
Lunghezza d'onda 905 ± 20 nm
11
Corrente massima 15 A
Potenza di picco (minima) 12 W
Tempo di funzionamento (massimo) 200 ns
Frequenza di ripetizione massima 5 kHz
3.3.3. Rivelazione del segnale di collettore
Per rivelare il segnale di collettore Vc serve un buon oscilloscopio con sensibilità
massima di alcuni milliVolt. E' necessario prelevare Vc attraverso un preamplificatore
differenziale che permetta di sottrarre dal segnale di collettore la frazione V* del
segnale di spazzolamento che si vede al collettore 6 , in modo che l'oscilloscopio
amplifichi solo il piccolo segnale dovuto all'iniezione di portatori in eccesso (figura 9).
Figura 9: A sinistra: impulso raccolto (traccia 1) e tensione di spazzolamento (traccia 2)
A destra: uscita del differenziale (traccia 1) e impulso di trigger (traccia2)
Lo schema del preamplificatore è riportato nella figura 10. Esso utilizza un
amplificatore operazionale OP07, che esegue la differenza fra la tensione VC
proveniente dalla punta (collettore) e la tensione αVS (con α regolabile fra 0 e 1)
proveniente dall’impulsatore di Sweep.
6
La frazione α è data dalla relazione α =xc/l , dove xc è la distanza del collettore dall'estremità del
cristallo posta a terra.
12
Figura 10: Preamplificatore differenziale
La scelta dei valori delle resistenze nel partitore di VC e nella rete di retroazione è fatta
in modo di ridurre di un fattore 3 le tensioni agli ingressi dell’AO (tensioni di
alimentazione ±15V).
4. Raccolta ed analisi dei dati
L’ampiezza dell’impulso raccolto al collettore dipende dalla "pulizia" della superficie
del cristallo. Infatti in cristalli di dimensioni modeste la ricombinazione avviene in
prevalenza negli strati superficiali ed è tanto più rapida quanto più numerosi sono i
difetti reticolari dovuti al taglio ed alle successive manipolazioni della superficie.
Importante è soprattutto il contatto a punta: se il segnale all'oscilloscopio appare
disturbato ed instabile , può essere utile affilare la punta dell’ago con carta vetrata fine,
o condizionare il contatto con vibrazione meccanica (spesso basta un gentile
tambureggiare con il dito sul portacampione per stabilizzare un contatto rumoroso).
4.1. Misura della distanza d tra emettitore e collettore
Si può fare direttamente con un calibro, o leggendo la scala millimetrata posta sopra le
slitte. Le distanze utili per l'esperimento vanno da un paio di mm a 10 mm o poco più.
Si riesce ad apprezzare 1/4 di mm per cui l'errore su d va da ≈10% a ≈2% .
4.2. Valore del campo di spazzolamento E
Si ottiene come rapporto tra la d.d.p. VS, prodotta dal primo impulsatore e visualizzata
su uno dei canali dell'oscilloscopio, e la lunghezza l del cristallo che si può misurare
mediante un calibro ventesimale. Nel far ciò si assume che il cristallo sia omogeneo, e
13
che inoltre le resistenze dei contatti terminali siano trascurabili rispetto alla resistenza
del cristallo 7
4.3. Misura del tempo di volo t
Nella determinazione del ritardo t fra i due impulsi e della larghezza a metà altezza Δt si
osserverà che, riducendo l’intensità (o la durata) dell'impulso di iniezione (a parità di
distanza d e di campo di spazzolamento Es) t e Δt diminuiscono un poco. Pertanto
conviene fare una serie di misure di t e Δt, riducendo gradualmente VL fino a che i
valori di t e Δt rimangono costanti (figura 11).
Figura 11: Segnali di collettore per diverse ampiezze della tensione di polarizzazione del laser VL. La
distanza tra fibra e collettore è 5 mm e l’intensità del campo di spazzolamento è ES=6V/cm.
Determinato in questo modo il massimo valore usabile dell’intensità dell’impulso
luminoso si può procedere ad una serie di misure di tempo di volo a distanza d fibracollettore costante al variare della tensione di spazzolamento VS. (Figura 12)
7 Per verificare la validità di queste ipotesi si può misurare con l'oscilloscopio come varia la d.d.p. V (x)
C
fra l'estremo del cristallo posto a terra e il collettore (togliendo l'iniettore) in funzione della distanza x fra
l'estremo del cristallo ed il collettore. Il campo di spazzolamento è definito punto per punto da E(x)=ΔVC
(x)/Δx. Se E(x) così misurato risulta costante al variare di x la prima assunzione è valida. Se inoltre il
valore così ottenuto coincide entro gli errori con VS/l anche la seconda assunzione è valida.
14
Figura 12: Esempio di serie di segnali di collettore registrati con diverse ampiezze della tensione
spazzolamento VS. La distanza tra fibra e collettore è 5 mm
Dai dati riportati in figura 12 si ricavano i valori riportati in tabella I: i valori delle aree
A e delle larghezze Δt sono stati ottenuti mediante interpolazione gaussiana
dell’impulso (cfr. Appendice 3).
Vs (V)
t (μs)
A (V μs)
Δt (μs)
Es (V/cm)
μ(cm2/Vs)
ln(A)
8
51.24
18.11
50.83
2.286
4355
3.928
10
43.67
15.17
78.19
2.857
4087
4.359
15
29.80
8.550
146.5
4.286
3993
4.987
20
23.64
6.057
210.3
5.714
3775
5.349
25
19.36
4.627
250.9
7.143
3688
5.525
30
16.30
3.620
276.5
8.571
3650
5.622
Tabella I: Misure ottenute con d costante al variare di VS
15
4.4. Valutazione della vita media di ricombinazione
Un grafico del logaritmo naturale dei valori A delle aree sottese dall’impulso in
funzione del tempo di volo è riportato in figura 13. La pendenza della retta che interpola
i dati misura il reciproco della vita media τ.
Figura 13: ln(A) in funzione di t: il reciproco della pendenza della retta interpolante misura la vita media
(costante di tempo del decadimento dell’area)
4.5. Una prima valutazione della mobilità
I valori della mobilità elettronica calcolati dai tempi di volo misurati a distanza fissa per
diversi valori del campo di spazzolamento mostrano una sistematica dipendenza dal
campo elettrico (figura 14) e forniscono un valor medio di (3924±270) cm2V-1s-1. Tale
valore è inoltre affetto dalla elevata incertezza nella misura di d (5.1 mm).
16
Figura 14 : la mobilità calcolata per d=0.51 cm per vari valori di VS.
4.5. Misure di mobilità a campo di spazzolamento costante
Si può eseguire una serie di misure dell’impulso di collettore mantenendo fisso il valore
della tensione di spazzolamento e variando invece la distanza d fibra-collettore (Tabella
II).
d (cm)
1.24
1.05
0.95
0.85
0.7
0.6
0.5
0.4
t (μs)
98
84
80
69
58
50
41
33
vd(cm/s)
12602
12499
11875
12318
12068
12000
12195
12121
μ (cm2/Vs)
4221
4187
3978
4126
4043
4020
4085
4060
Δt (um)
25.1
27.0
25.6
24.1
22.8
22.3
17.7
16.3
(d Δt) 2
9.62e-10
8.02e-10
5.91e-10
4.19e-10
2.54e-10
1.79e-10
7.81e-11
4.24e-11
t3
9.41e-13
5.93e-13
5.12e-13
3.29e-13
1.95e-13
1.25e-13
6.89e-14
3.59e-14
Tabella II: misure ottenute con Vs=10 V , variando la distanza d
I valori della mobilità in funzione della distanza fibra-collettore sono riportati nel
grafico di figura 15.
17
Figura 15: Mobilità calcolata da misure effettuate con VS=10V e con diversi valori di d
4.6. Valutazione del coefficiente di diffusione D
Si può ottenere, ricorrendo alla relazione [4] (vd Δt)2 = 11.08 D t, tramite la misura
della larghezza a metà altezza dell'impulso di collettore. Poiché vd =d/t tale relazione si
può anche scrivere:
( d Δt )2 / 11.08 = D t 3
[6]
e riportando il quadrato del prodotto d Δt in funzione di t3 per diversi valori del ritardo t
e della distanza fra le punte d si ha una retta la cui pendenza determina D (figura 16).
Conviene, in questo tipo di interpolazione, utilizzare dati ottenuti con diversi valori
della distanza d per evitare un rilevante errore sistematico introdotto dalla incertezza su
un singolo valore della distanza d.
Figura 16: Grafico di (d Δt)2 in funzione di t3
18
Dal grafico di figura 16 si vede che la proporzionalità è ben verificata e si ricava per il
coefficiente di diffusione degli elettroni De = (98±4) cm2/s.
Altrimenti si può calcolare il rapporto D/μ mediante la formula :
[7]
D/μ = (VSd/11.08 l ) (Δt/t)2
che si ottiene dalla [4] sostituendo vd2 con (d/t)μES. Il valore così trovato va
confrontato con quello fornito dalla relazione di Einstein D/μ= kT/e = 0.026 Volt (a
T=300K).
I dati di tabella I danno per D/μ un valore medio D/μ=(0.0258±0.0031) eV in buon
accordo con il valore 0.026 previsto .
4.7. Errore sistematico nella misura di μ
La dipendenza sistematica dal campo di spazzolamento dei valori calcolati per la
mobilità è dovuto alla diffusione e ricombinazione dei portatori, effetti che si fanno
sentire maggiormente per piccoli valori di VS (su tempi di volo più lunghi l’impulso si
allarga e l’ampiezza diminuisce maggiormente).
Una spiegazione qualitativa di questo effetto si ha pensando al fatto che se la vita media
fosse abbastanza grande si potrebbe osservare (per effetto della sola diffusione) un
picco molto largo al collettore persino con campo di spazzolamento nullo, ovvero si
misurerebbe a campo zero una mobilità infinita . Infatti se l’impulso diffonde soltanto,
(con velocità di deriva nulla) dopo un certo tempo si osserverebbe un aumento di
portatori al collettore, seguito da un decremento finale (distribuzione uniforme).
Una analisi quantitativa è stata effettuata da J.P McKelvey 8 , che ha ottenuto una
semplice formula correttiva:
μcorretta = μ ( 1 + x 2 -x)
nella quale il parametro x ha l'espressione:
2kTl
x=
(t / τ + 1/ 2)
eVS d
[9]
[10].
Assumendo per la vita media di ricombinazione il valore τ=20 μs, suggerito dalle
misure di area dell'impulso riportate in figura 13, si trovano valori di μcorretta che anche
ai bassi valori di VS sono molto meno dispersi attorno al valore medio (Figura 17). Il
valor medio risulta per μcorretta (3678±77) cm2V-1s-1.
8
J.P.McKelvey : Diffusion effects in drift mobility measurements in semiconductors, Journal of Applied
Physics 27,341 (1956)
19
Figura 17 : Mobilità di deriva in funzione della tensione VS (per d=0.51 cm). Tondi pieni: valori
misurati. Tondi vuoti: valori corretti con le relazioni (9-10)
4.7. Controllo della temperatura del campione
Se la durata dell'impulso di tensione è lunga (duty cycle maggiore del 10% circa) e la
tensione di spazzolamento elevata (>30 V circa) il campione si riscalda e quindi la
mobilità di deriva diminuisce.
La mobilità dipende dalla temperatura come μ = cost T-α , quindi Δμ(Τ)/μ ≈ -α ΔT/T.
Ad esempio per un campione di Ge drogato P , per il quale α≈2.3, si ha una
diminuzione della mobilità degli elettroni, che a T≈300 K vale μe=3900 cm2V-1s-1, Δμe
= α μe (ΔT/300) ≈ 30ΔT cm2V-1s-1 per un incremento della temperatura di circa 10
gradi.
20
Appendice 1 : Contatti metallo-semiconduttore (S. Wang, rif. 1)
Le superfici libere dei campioni di semiconduttore sono ricoperte da un sottile (1-2 nm)
strato di ossido. A causa della diversa struttura cristallina e del diverso passo reticolare
fra lo strato di ossido ed il semiconduttore sottostante si producono imperfezioni
strutturali e questi creano livelli energetici (stati superficiali) permessi entro la banda
proibita del semiconduttore, sia per elettroni che per lacune.
Se abbiamo un contatto metallo-ossido-Ge N gli stati superficiali catturano alcuni
elettroni liberi dall'interno del Ge, si forma quindi un doppio strato di cariche: negative
in superficie, positive (cariche fisse degli ioni donori) all'interno. Si crea cioè una
barriere di potenziale simile a quella di una giunzione PN ma con la differenza che le
cariche negative sono solo in superficie mentre quelle positive sono distribuite entro
uno strato esteso all'interno del semiconduttore.
Se dall'esterno si applica una tensione con il metallo negativo rispetto al semiconduttore
la barriera aumenta e quindi non si ha passaggio di corrente (di portatori maggioritari,
cioè elettroni). Viceversa se si fa positivo il metallo e negativo il semiconduttore la
barriera si abbassa e si ha corrente di diffusione. La situazione corrisponde ad un diodo
con l'"anodo" dalla parte del metallo ed il "catodo" dalla parte del semiconduttore.
Invece per un contatto metallo-ossido-Ge P gli stati superficiali catturano lacune
dall'interno del semiconduttore e le polarità del doppio strato e del diodo sono
rovesciate.
Appendice 2: Diffusione dei portatori in eccesso
Un fenomeno che contribuisce a ristabilire le condizioni di equilibrio in un
semiconduttore soggetto ad iniezione di cariche in eccesso è la diffusione .
Infatti se i portatori vengono iniettati localmente (cioè non uniformemente distribuiti nel
volume del campione) essi tendono a diffondere dalle regioni ove la concentrazione è
maggiore a quelle dove la concentrazione è minore.
In assenza di campi elettrici esterni, e per piccole perturbazioni, il fenomeno è descritto
da una semplice equazione di conservazione della carica: j = –D grad n, ove j è il
flusso [numero/(cm2 s)] di portatori, n la loro concentrazione (numero/cm3) e D è il
coefficiente di diffusione che ha le dimensioni di un'area per unità di tempo (cm2 s-1).
Risolvendo l'equazione di trasporto di Boltzmann, si ricava l'espressione approssimata :
D=<v>λ/3, dove <v> è la velocità media termica dei portatori e λ il loro cammino
libero medio. Poiché λ≈<v> tc dove tc è il tempo medio che separa due collisioni, e
<v>≈√(3kT/m) si può riscrivere D in funzione di tc : D≈kTtc/m .
Se poi si ricorda che anche la mobilità μ è funzione di tc e di m ( modello di Drude:
μ = etc/m), si ottiene la relazione di Einstein:
D/μ = kT/e
21
L'equazione di continuità per i portatori minoritari in presenza di generazione,
ricombinazione e diffusione, può essere scritta (con l’assunzione che di debole
perturbazione della densità di portatori all’equilibrio Δn<<no) nel caso
unidimensionale:
∂n/∂t = –(1/e) ∂J/∂x – n/τ +( G )
ove G è la velocità di generazione (ad esempio per iniezione ottica), τ la vita media
dovuta a ricombinazione e J la densità di corrente:
J = -e D∂n/∂x + e μ n Ex
J è la somma di un termine dovuto alla diffusione (proporzionale al gradiente di densità
lungo x) e di un termine di deriva (proporzionale alla componente Ex del campo
elettrico).
Risolvendo l’equazione di continuità nel caso di campo elettrico esterno nullo (Ex =0),
con iniezione di No cariche a t=0 nel punto x=0, il risultato è una funzione gaussiana:
n(x,t) = (No /√(4πDt)) exp {-t/τ} exp{-x2/(4Dt)}
funzione la cui larghezza a metà altezza Δx è:
(Δx)2=16 ln2 D t = 11.08 D t.
Appendice 3: Trasferimento dell’impulso per interpolazione gaussiana su PC
La forma dell’impulso che appare sullo schermo dell’oscilloscopio digitale può essere
memorizzata in un Personal computer se l’oscilloscopio è dotato di interfaccia (ad
esempio gli oscilloscopi Tektronix della serie TDS1000, GWInstek della serie
GDS2000 o Hameg HM507).
Figura 18: a sinistra singola acquisizione, a destra media su 64 acquisizioni
Il rapporto segnale/rumore può essere notevolmente aumentato se si dispone della
possibilità di mediare su molti impulsi raccolti, come mostrato in figura 18.
22
L’immagine sullo schermo dell’oscilloscopio digitale è una matrice bidimensionale ove
i pixel corrispondenti all’impulso sono colorati diversamente dagli altri. I formati più
comuni per trasferimento del contenuto dello schermo a PC sono di tipo grafico
(bitmapped, ad esempio BMP, jpg…) oppure numerico (valori separati da virgola, come
CVS o caratteri ASCII, tipo TXT). Nel secondo caso l’impulso viene memorizzato
come una matrice a due colonne, ove la prima colonna contiene i valori delle ascisse dei
pixel che descrivono la traccia (tempi) e la seconda i valori delle corrispondenti
ordinate (tensioni).
Un opportuno software per analisi grafica (ad esempio Origin o Kaleidagraph) può
consentire una facile manipolazione dei dati, includente la sottrazione di una retta
inclinata (baseline subtraction) nel caso l’impulso sia deformato dalla perturbazione
dovuta all’accensione del campo di spazzolamento, e una interpolazione mediante
funzione gaussiana.
La figura 19 mostra un esempio di analisi mediante Origin.
Figura 19: l’impulso raccolto analizzato in Origin, con indicazione dell’istante di trigger e della baseline
da sottrarre prima di eseguire l’interpolazione con una funzione gaussiana
Appendice 4: Dati sperimentali reperibili in letteratura
Ge*
Ge**
Si*
Si**
μe
Valori a 300K
μh
(cm2/Vs)
3900±100
3900
1400±100
1400
De
Dh
(cm2/Vs)
(cm2/s)
(cm2/s)
1900±50
1900
470±15
450
101
100
36
36
49
50
12
12
*) M.B.Prince, Phys. Rev. 92, 681 (1953) e Phys. Rev. 93, 1204 (1954) e G.W.Ludwig, R.L.Watters,
Phys. Rev. 101,1699 (1956). I valori dei coefficienti di diffusione D (cm2/s) sono stati ottenuti come
D=μ(kT/e).
23
**) http://www.ioffe.rssi.ru/SVA/NSM/Semicond/Si/electric.html#Basic
Riferimenti
1. S.Wang Fundamentals of Semiconductor Theory and Device Physics, Prentice Hall,
(1989)
2. J.P.McKelvey, J. App. Phys. 27,341 (1956)
3. H.B.Prince, Phys. Rev. 92,681 (1953) and Phys.Rev. 93,1204 (1954)
4. A.Sconza and G.Torzo Eur.J.Phys.8, 34-40 (1987)
5. A. Sconza, G. Galet and G. Torzo Am. J. Phys, 68, 80-87 (2000)
6. S. M. Sze, Physics of Semiconductor Devices John Wiley and Sons (1981)
24