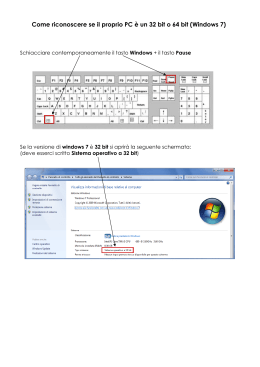
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
Codifica dei numeri REALI (RAZIONALI E IRRAZIONALI) con segno in base 2:
• Rappresentazione in virgola fissa (lezione precedente)
• Rappresentazione in virgola mobile (Foating Point)
Rappresentazione virgola mobile (Floating Point)
• La rappresentazione in virgola fissa non si presta a
rappresentare numeri molto grandi (es. 567 000 000000) o
molto piccoli (es. 0,0000000000000915)
• Per ovviare a ciò si utilizza la rappresentazione in virgola
mobile (floating point), detta anche a mantissa e
caratteristica.
• Questo tipo di notazione si basa sulla rappresentazione
esponenziale dei numeri, detta anche notazione scientifica.
• Secondo tale notazione un numero reale N può essere
espresso nella seguente forma:
N = (-1)s * m * 2esp
Dove
s = segno 0 => + 1=> m = mantissa
esp = esponente o caratteristica
1
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
Formato floating point standard IEEE 754
lo standard internazionale più diffuso e quello stabilito
dall'IEEE (Institute for Electrical and Electronics Engineering)
identificato dalla sigla IEEE 754. Questo standard prevede
tre formati principali di rappresentazione
• l’esponente deve essere polarizzato ossia
Al valore dell’esponente originario occore sommare un certo
valore fisso detto bias 2n-1-1
Formato
Singola
precisione
Doppia
precisione
Quadrupla
precisione
N bit
Segno
32
1
4 bytes
64
1
8 bytes
Esponente
8
Mantissa
23
bias
127
11
52
1023
128
1
8 bytes
15
112
16383
Facciamo esempio Singola precisione
• 1 bit per il segno
• 8 bit per l’esponente polarizzato biased 127 (si dice anche eccesso 127)
• 23 bit per la mantissa
normalizzata con la prima cifra significativa alla
sinistra del punto con hidden bit ovvero nella forma 1.XXXXXXXXX…X
1 prima della virgola viene omesso
2
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
Esempio 1
Rappresentare in singola precisione (32 bit) il numero reale 43,6875
IL NUMERO È POSITIVO BIT 31 = 0
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
0
Covertiamo la parte intera
DIVIDENDO
43
21
10
5
2
1
(43)1o=(101011)2
DIVISORE
2
2
2
2
2
2
QUOZIENTE
21
10
5
2
1
0
RESTO
1
1
0
1
0
1 (bit + significativo)
Covertiamo la parte frazionaria
(0,6875)1o
fattore1
0,6875
0,375
0,75
0,5
fattore2
2
2
2
2
prodotto
1,375
0,75
1,5
1
(0,6875)1o=(0,1011)2
3
parte frazionaria
0,375
0,75
0,5
0
parte intera
1 (bit + significativo)
0
1
1
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
Dunque (43,6875)10 = (101011,1011)2
Normalizziamo il numero binario ottenuto
In modo che la forma sia 1.xxxxxx
(101011.1011)2 = 1, 010111011*25
La parte intera non la considero (hidden bit o bit nascosto, o bit implicito)
MANTISSA 010111011
COMPLETO a 23 bit (aggiungo tanti 0 a destra )
01011101100000000000000
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
0
0 1 0 1 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Infine
ESPONTENTE = 5 in binario
Devo polarizzarlo aggiungendo bias 127 => 5 +127 = 132
(132)10 = (10000100)2
Risultato
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
01000010001011101100000000000000
4
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
Esempio 2
Rappresentare in singola precisione (32 bit) il numero reale -0,75
IL NUMERO È NEGATIVO BIT 31 = 1
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
1
Covertiamo la parte intera
(0)1o=(0)2
Covertiamo la parte frazionaria
(0,75)1o
fattore1
0,75
0,5
fattore2
2
2
prodotto
1,5
1
parte frazionaria
0,5
0
parte intera
1 bit + significativo
1
(0,75)1o=(0,11)2
Dunque (-0,75)10 = (-0,11)2
Normalizziamo il numero binario ottenuto
In modo che la forma sia 1.xxxxxx
(-0,11)2= - 1, 1*2-1
La parte intera non la considero (hidden bit o bit nascosto, o bit implicito)
5
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
MANTISSA 1
COMPLETO a 23 bit (aggiungo tanti 0 a destra )
10000000000000000000000
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
0
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Infine
ESPONTENTE = -1 in binario
Devo polarizzarlo aggiungendo bias 127 => -1 +127 = 126
(126)10 = (1111110)2
COMPLETO A 8 BIT (aggiungo 0 a sinistra)
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
00111111010000000000000000000000
6
INFORMATICA Dicembre 1BSA 2014 Docente Salvatore Mosaico parte 2
Rappresentazione casi particolari
Lo zero
Valore
zero
Infiniti
Nan (not a number)
Segno
0
0/1
Esponente
0
255
255
Mantissa
0
0
Diverso da 0
Zero
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
00000000000000000000000000000000
Infinito segno 1 –infinito 0 + infinito
3
1
3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
0
/
1
1111111100000000000000000000000
NaN
3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 9 8 7 6 5 4 3 2 1 0
1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
11111111
almeno un bit a 1
7