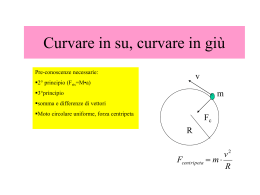
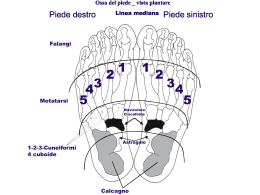
3. Biomeccanica
1
Momento di una forza
O

b
P

F
Si definisce momento di una forza F rispetto ad un
punto O il prodotto vettoriale
  
M = b ∧F
2
Ricordi il prodotto
vettoriale????
3
Prodotto Vettoriale
Il prodotto vettoriale è un’operazione vettoriale che
associa a due vettori un altro vettore. Il risultato
dell’operazione è, dunque, un VETTORE. Ne segue che
dovremo conoscerne MODULO, DIREZIONE e VERSO e
NON SOLO IL MODULO
IL RISULTATO è
un VETTORE
b
α
a
4
Il modulo del vettore risultante è:
c= a b sinα
La direzione del vettore risultate è quella della
perpendicolare al piano individuato dai vettori a e b.
c
b
α
a
5

M
O
α

F

b
Il momento di una forza F è un vettore perpendicolare al
piano individuato dalla forza e dal braccio della forza il cui
verso è dato dalla regola della mano dx e di modulo pari a:

 
M = F b sin α
6
Dimensioni [M] = [F] [L]=[L2][M][T-2]
Unità di misura: [SI] newton (N) × metro (m)= m2.kg.s-2
7
Condizioni di equilibrio roto-traslatorio di un corpo
1. Equilibrio Traslazionale


FRIS = ma = 0
(FRIS)x=m ax=0
(FRIS)y=m ay=0
(FRIS)z=m az=0
1 equazione vettoriale
3 equazioni scalari
2. Equilibrio Rotazionale

MRIS =
n
∑
i =1
 
Mi = bi ∧ Fi = 0
(MRIS)x=0
(MRIS)y=0
(MRIS)z=0
1 equazione vettoriale
3 equazioni scalari
8
Condizioni di equilibrio roto-traslazionale per un
corpo rigido
(FRIS)x=0
(FRIS)y=0
(FRIS)z=0
(MRIS)x=0
6 Equazioni scalari
(MRIS)y=0
(MRIS)z=0
9
Approssimazione per gli equilibri nel corpo umano
Una buona approssimazione consiste nel considerare le
forze tutte giacenti in un piano verticale (x,y). In questo
modo accade che:
y
F e b sono nel piano xy
(FRIS)x=0
Fris
(FRIS)y=0
(FRIS)z=0
(MRIS)x=0
o
(MRIS)y=0
(MRIS)z=0
z
b
x
Mris ⁄⁄ asse z
10
Equilibrio dell’articolazione dell’anca
L’articolazione dell’anca è costituita dalla testa del femore che si
inserisce nella cintura pelvica in una cavità detta acetabolo. Tra la testa
del femore e l’acetabolo ci sono cartilagini che garantiscono il movimento
quasi senza attrito.
11
Consideriamo un uomo in equilibrio su un piede solo
Bilancio delle Forze
1) La Forza peso della gamba, Pg è
diretta verticalmente verso il basso, è
applicata nel baricentro della gamba e
ha modulo pari a 1/7 della forza peso
del corpo.
2) La Reazione vincolare, N, offerta
dal suolo, diretta verticalmente verso
l’alto e di modulo pari alla forza peso.
3) La Forza R cha agisce sulla testa
del femore che tiene conto della
forza peso del corpo (senza la gamba
sottostante).
4) La Forza F di trazione dei muscoli
abduttori (glutei) che agiscono sul
troncatere maggiore. Questa forza ha
modulo incognito ma è diretta verso
l’alto formando un angolo di circa 70°
con l’orizzontale.
12
Rispetto a quale punto calcoliamo i momenti delle forze?
Ora devi introdurre un sistema di riferimento in cui studiare l’equilibrio
dell’articolazione. Come sai il sistema di riferimento è arbitrario e lo
scegli arbitrariamente per cercare di rendere più semplici i calcoli che
andrai a fare
y
Sceglierai
x
sicuramente
il punto O coincidente
con la testa del femore.
In questo modo il
momento della forza R
sarà nullo (il braccio
della forza è nullo)
13
14
3
Riprendiamo le
condizioni di equilibrio
roto-traslazionale:
(FRIS)x=0
(FRIS)y=0
(MRIS)z=0
E vediamo come utilizzare nel caso
dell’articolazione dell’anca
15
La condizione di equilibrio roto-traslazionale si riduce alle 3 equazioni scalari
(1)
(FRIS)x= Pgx + Rx + Fx + Nx=0
(2)
(FRIS)y= Pgy + Ry + Fy + Ny=0
(3)
(MRIS)z = (MPg)z + (MN)z + (MF)z + (MR)z=0
che divengono:
Fcos70°- Rx=0
(1)
Fsin70°- Ry-1/7 p +p=0
(2)
Fsin70°×(7cm) -p× (11 cm)+1/7p× (3cm) +0=0
Dalla (3) si ottiene:
F~1.61 p
Lo sforzo dei muscoli abduttori (glutei)
dipende dalla massa corporea !!!!
16
(3)
Momento della forza F
  

(MF )Z = bF ∧ F = bF × F × sin α
y
F
z
bF
α=(180-70)°
(MF)z
bF
x
(MF)Z= bF×F×sin(180-70)= (7cm) × F× sin(70)
17
Momento della forza Pg




(MPg )Z = bPg ∧ Pg = bPg × Pg × sin α
y
z
α
bPg
(MPg)z
x
Pg
α
bPg
α
bPg× sinα= 3 cm
(MPg)Z= Pg × bPg× sinα= Pg× 3 cm
18
Momento della forza N

 

(MPg )Z = bN ∧ N = bN × N × sin α
y
z
bN
N
(MN)z
α
x
bN
bN× sin(180-α)= 11 cm
(MN)Z=N× bN× sinα = N× bN× sin(180-α) = N × 11 cm=
-
19
p × 11 cm
Dalla (3) si ottiene:
La sforzo dei muscoli abduttori (glutei)
dipende dalla massa corporea !!!!
F~1.61 p
Sostituendo la relazione precedente nella (1) e nella (2) si ottiene:
Rx~ 0.55 p
Ry~ 2.37 p
R = (Rx ) + (Ry ) ≈ 2.5p
2
2
La forza che agisce sulla testa
del femore è pari a circa due
volte e mezza la forza peso
corporea!!!
20
Determinate le componenti cartesiane possiamo
anche calcolare l’orientamento della forza R che
agisce sulla testa del femore
RX = R cos θ
⎛ RX ⎞
θ = arccos⎜ ⎟ ≈ 76.9°
⎝ R ⎠
21
Perché è importante determinare l’angolo?
1) E’ determinante perché il tessuto osseo cresce nella
direzione dello sforzo applicato. Questo comporta una
deviazione della testa del femore rispetto al femore
2) In caso di una frattura del femore, la forza dei muscoli
abduttori si indebolisce (F→0) con la conseguenza che R è
diretta più verticalmente. La testa del femore cresce più del
dovuto in verticale
(R)x= Fcos70°=0
(se F→0)
Con un conseguente allungamento dell’arto il quale
produce una rotazione della cintura pelvica con conseguente
22
curvatura della colonna vertebrale (scoliosi)
E se hai la scoliosi o
quando hai/avrai
l’articolazione logora a
cosa ti serve/servirà
un BASTONE ???
23
Valutare la forza F degli adduttori e la forza R
agente sulla testa del femore
Sul bastone si scarica 1/6 della
forza peso
La forza peso residua (5/6 p) è applicata al
baricentro corporeo
La reazioni vincolari offerte dal suolo al corpo e al
bastone saranno chiaramente in modulo pari a:
Np=5/6 p
Nb= 1/6 p
24
Qual è la distanza tra l’asse baricentrale e la
forza Np?
(MNp)z +(MNb)z=0
Np×d - Nb×(30 cm) =0
d = (Nb/Np)×(30 cm) =6 cm
25
Ora è sufficiente ripetere la stessa
procedura seguita per il calcolo di F e R
nel caso dell’articolazione dell’anca di un
uomo in equilibrio su un piede solo.
(FRIS)x= Pgx + Rx + Fx + Npx=0
(FRIS)y= Pgy + Ry + Fy + Npy=0
(MRIS)z = (MPg)z + (MNp)z + (MF)z + (MR)z=0
I momenti delle forze si intendono
calcolati rispetto alla testa del femore
26
Fcos70°- Rx=0
Fsin70°- Ry - 1/7 p + 5/6 p=0
Fsin70°×(7cm) +1/7p× (3cm)-5/6 p× (18-7-6) cm =0
Ora è solo algebra e puoi
facilmente verificare che:
F~0.64 p
Lo sforzo richiesto ai muscoli
adduttori è notevolmente
inferiore rispetto a quello
necessario per stare in
equilibrio su un piede solo
(F~1.61 p) !!!
27
Rx~ 0.22 p
Ry~ 1.29 p
R = (Rx ) + (Ry ) ≈ 1.31p
2
2
⎛ RX ⎞
θ = arccos⎜ ⎟ ≈ 80.3°
⎝ R ⎠
La forza sulla testa del
femore è circa la metà di
quella che si ha in
equilibrio su un piede solo
(deambulazione, corsa)
L’angolo è circa lo stesso
28
Equilibrio del piede in sollevamento
Consideriamo il caso dell’equilibrio su un singolo piede. Assumiamo che
venga alzato il calcagno. L’obiettivo è quello di calcolare la forza
applicata dal tendine d’Achille sul calcagno quando il peso del corpo si
scarica sulla pianta del piede.
Bilancio delle Forze che agiscono
sul piede in sollevamento
1) La FT è la forza applicata dal tendine al
calcagno.
2) La Forza F0 che viene esercitata dalle
ossa della gamba (fibula e tibia) sul piede
3) La Reazione vincolare FP offerta al
piede dal suolo, diretta verticalmente
verso l’alto e di modulo pari alla forza peso.
E la forza peso del
piede?
29
10 cm
Le due condizioni di equilibrio traslazionale sono:
(FRIS)x= (FT )x + (F0 )x + (FP )x =0
(FRIS)y= (FT )y + (F0 )y + (FP )y =0
Che divengono:
(FT ) sin7°- (F0 ) sinθ =0
(FT )cos7°- (F0 ) cosθ + FP =0
30
La condizione di equilibrio rotazionale sarà:
(MRIS)z = (MFT)z + (MF0)z + (MFP)z =0
Che diviene, se scegliamo come polo per il calcolo dei
momentiil punto di applicazione della forza F0:
10cm × (FP) -5.6 cm × (FT ) cos7° =0
Dalla quale, se fai bene i calcoli (periodo ipotetico del
1°tipo?), troverai:
FT =1.8 FP
Il tendine d’Achille è sottoposto a sforzi
rilevanti dovendo sopportare una tensione pari a
circa due volte la forza peso
Tendiniti, ispessimenti, rottura: Se FT diventa piccola nessuna forza
31
bilancia F0 e quindi non si riesce a sollevare il piede
Che, introdotta nelle prime due, ti darà (se non ti vengono i
calcoli, li faremo insieme):
F0 =2.8 FP
θ~ 4.5°
La forza che la gamba esercita sul piede ha
modulo quasi tre volte la forza peso ed è
diretta quasi lungo la verticale
Tendiniti, ispessimenti, rottura: Se FT diventa
piccola nessuna forza bilancia F0 (che è grande
in modulo) e quindi non si riesce a sollevare il
piede
32
Equilibrio tronco-vertebrale
Consideriamo un uomo in posizione eretta (in equilibrio, questa volta, su
entrambi i piedi). Qual è l’intensità della forza muscolare esercitata dai
muscoli dorsali?
Bilancio delle Forze che assicurano
l’equilibrio del tronco
1) FP è la forza peso applicata al baricentro. Il baricentro
corporeo si trova in posizione anteriore rispetto alla
spina dorsale.
2) Lo sforzo compressionale R che agisce sulla settima
vertebra della colonna vertebrale dovuto al fatto che il
tronco poggia sulla colonna vertebrale.
3) La forza muscolare Fm offerta dai muscoli dorsali
33
La condizione di equilibrio roto-traslazionale si riduce alle 3 equazioni scalari
(FRIS)x= (Fm)x + Rx + (FP)x =0
(FRIS)y= (Fm )y + Ry + (FP)y =0
(MRIS)z = (MFm)z + (MR)z + (MFp)z =0
che divengono:
R = Fm + FP
Fm a = bFP
34
Fm =(b/a)FP~2FP
R = Fm + FP ~ 3FP
1. Quanto più il baricentro è allineato con la colonna
vertebrale (b assume il minimo valore possibile) e tanto
minore sarà lo sforzo richiesto ai muscoli dorsali e lo
sforzo compressionale vertebrale
2. In caso di sovrappeso il baricentro è spostato in avanti
(b aumenta) e quindi per soddisfare l’equilibrio rotazionale
lo sforzo richiesto ai muscoli dorsali aumenta così come
aumenta lo sforzo compressionale vertebrale
35
La frattura della tibia dello sciatore
Il piede e l’anca di uno sciatore di massa m=70
kg sono bloccati, mentre viene meno l’appoggio
dell’altro piede. Il corpo tende a ruotare
attorno ad un asse passante per la tibia (vedi
figura) nel piano della figura. La tibia può
sopportare un massimo momento flettente pari
a M=(πr3/4) × Σ dove con Σ indichiamo lo
sforzo compressivo. Qual è la massima distanza
di cui il baricentro può spostarsi rispetto alla
tibia prima che questa si fratturi (vedi sotto)?
(r=1 cm; Σ=2.1×108 Nm-2)
Tipica radiografia di una frattura per flessione
della tibia
36
L’equilibrio del piede in sollevamento per la
persona accovacciata
Nel caso di una persona
accovacciata la configurazione del
piede in sollevamento vista nella
slide 29 di questo capitolo si
modifica come in figura.
Determinare FT e F0 e confrontarle
in maniera critica con il caso
suddetto.
FT=13,54FP
F0=14.17FP
θ=41.2°
37
La tensione del legamento patellare
Sempre nel caso di una persona
accovacciata la parte inferiore della
gamba è mantenuta in posizione di
equilibrio dal legamento patellare
attaccato alla parte superiore della tibia e
che scorre sopra la rotula. Le forze agenti
sulla gamba inferiore sono quelle mostrate
in Figura. Si assuma FP=40 kgpeso e Pg= 10
kg peso . Determinare il modulo della
tensione T cui è sottoposto il legamento.
nonché direzione e modulo di R.
Il punto di applicazione della tensione
coincida con il punto su cui agisce R. La
gamba inferiore forma un angolo di circa
45° con la direzione orizzontale.
38