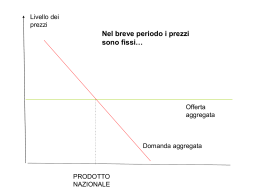
Corso di Economia Politica
prof. S. Papa
Lezione 29:
Modello Domanda-Offerta
Aggregata (AD-AS)
Facoltà di Economia
Sapienza Roma
Introduciamo i prezzi
• Finora abbiamo ipotizzato che i prezzi fossero dati e
costanti. Si trattava di una ipotesi semplificatrice che
poteva valere nel breve periodo
• Nel medio periodo le imprese variano i prezzi e si può
avere inflazione.
• Per determinare i prezzi è necessario introdurre
l’offerta aggregata, ovvero esplicitare il lato della
produzione.
• Infatti il prodotto non può essere aumentato all’infinito
se aumenta la spesa aggregata, ma vi sono dei vincoli
dal lato dell’offerta (disponibilità di risorse).
La domanda aggregata
• Occorre inoltre derivare la curva di domanda aggregata
nell’ipotesi che i prezzi non siano più rigidi, ma flessibili.
• Per distinguere la domanda aggregata in questo modello
dalla spesa aggregata del modello semplice la
chiameremo funzione macroeconomica della domanda
aggregata.
• La nuova curva AD che deriveremo ha un significato
diverso da quella vista nel modello semplice keynesiano.
• La nuova AD infatti è ottenuta dal modello IS-LM e
descrive come varia Y se i prezzi cambiano, assumendo
che vi sia equilibrio sia nel mercato dei beni sia in quello
delle attività finanziarie (moneta e titoli).
Variabili nominali e variabili reali
• Nel modello IS LM essendo i prezzi pari a 1 e fissi nel breve periodo
avevamo la coincidenza tra variabili nominali e reali. I simboli dei
modelli precedenti indicano, salvo esplicito avviso, variabili reali : Y è
il prodotto reale, C il consumo reale.
• Rimuoviamo l’ipotesi che P sono fissi (P) e P=1 .
Diventa rilevante la distinzione tra variabili nominali e variabili reali.
• VARIABILI NOMINALI: sono quelle espresse nell’unità di conto.
• VARIABILI REALI: sono quelle espresse in unità di prodotto nazionale.
Si ricavano dalle corrispondenti variabili nominali dividendole per P.
• ASSENZA DI ILLUSIONE MONETARIA: in coerenza con l’ipotesi di
razionalità, le scelte economiche dipendono dalle variabili reali e dai
prezzi relativi (che sono i prezzi in unità di conto divisi per P).
• Ci interessa di più il prodotto reale (da cui dipende
l’occupazione) di quello nominale.
4
Il modello IS-LM con P variabile
• Se vale l’ipotesi di assenza di illusione monetaria, nella IS non cambia
nulla, tutte le variabili sono reali:
• Y = m(Ā − br)
• Anche la domanda di moneta è espressa in termini reali:
• L = kY − hr
• Ma la banca centrale controlla l’offerta nominale di moneta (M).
• Perciò la LM va scritta così: M/P = kY − hr
• ossia offerta reale di moneta uguale a domanda reale di moneta.
• Risolvendo il modello col solito procedimento si arriva a:
• Y = m1Ā + m2M/P
• Risultato che mostra che P ha effetti reali : ΔP > 0 → ΔY < 0.
• La AD è una curva decrescente tra Y e P
5
AD e prezzi
• Poiché vogliamo isolare il solo effetto dei prezzi sulla AD,
nel modello IS-LM manterremo costanti tutte le altre
variabili che generalmente la influenzano (spesa
pubblica, tassazione, aspettative, etc.)
• Supponiamo di fissare un certo livello dei prezzi P0; a
tale livello dei prezzi viene costruita la curva LM. Dato lo
stock di moneta nominale, sarà il livello dei prezzi a
determinare lo stock di moneta reale che è dato da M/P.
• Partiamo pertanto da un equilibrio IS-LM con un livello
dei prezzi dato e pari a P0.
Riduzione dei prezzi in IS-LM
LM0(P=P0)
i
LM1 (P1<P0)
A
P0
A’
Una riduzione
dei
prezzi aumenta
M/P e sposta
verso il basso
la LM
IS
Y0
Y1
Reddito Y
Quando P ↓ allora Y ↑
La curva AD
LM(P0)
P ↓ da P0 a P1
P↓ M/P↑
e aumenta
la domanda aggregata
perché
c’e un effetto
ricchezza
i
LM(P1)
IS
Y0
P
P0
Y
Y1
A
A’
P1
AD
Y0
Y1
Y
Variazioni di P ed “effetto Keynes”
• Qual è il meccanismo di trasmissione da P a Y?
• Ricordiamo che P compare nella LM.
• Una diminuzione di P comporta un aumento dell’offerta
reale di moneta; perciò sposta in basso la LM e ha, di
conseguenza, un effetto espansivo sul prodotto Y.
• Il meccanismo di trasmissione è:
• ∆P<0, ∆Μ/P
∆Μ/ > 0, M/P>L, Bd > Bs, ∆Pb > 0, r < 0, ∆Ι > 0, Y>0
(effetto Keynes)).
• ∆P<0, aumenta ricchezza reale, ∆C > 0 (Effetto Pigou), Y >0
• Il meccanismo è lo stesso dell’effetto Keynes, ma è
innescato da ΔP.
9
Effetto ricchezza (Pigou)
• Ricchezza (o patrimonio) delle famiglie è il complesso del
valore dei beni, dei titoli e della moneta che esse
possiedono: PQ + B + M.
• Ricchezza Reale W: si ottiene dividendo la ricchezza per P:
• W= Q + (M+B)/P
• ΔP < 0 accresce la ricchezza reale, un suo aumento la
riduce.
• La ricchezza reale influenza positivamente il consumo. Ne
consegue che la diminuzione di P fa aumentare il consumo:
• Questo meccanismo di trasmissione è noto come:
• “Effetto Pigou”.
10
Inclinazione della AD
La funzione macroeconomica della domanda aggregata
mostra le combinazioni di prezzo e reddito per le quali
sia mercato monetario (titoli) che mercato dei beni sono
in equilibrio.
L’inclinazione negativa della nuova AD può essere così
spiegata:
• una riduzione di P aumenta l’offerta di moneta reale, il
tasso di interesse deve diminuire per mantenere in
equilibrio il mercato monetario, al diminuire di i gli
investimenti e quindi Y aumentano; ne consegue che una
riduzione di P provoca un ↑di Y
Spostamenti della AD
• Ogni mutamento, che non sia una variazione di P, e che
provoca spostamenti delle curve IS o LM determina
spostamenti anche della curva AD
• Pertanto spostano la curva AD:
- variazioni di G
- variazioni dell’offerta nominale di moneta (M)
- variazioni nella fiducia dei consumatori (C) o delle
aspettative degli investimenti (I)
- variazioni di T
• Se queste variazioni sono di tipo espansivo la curva AD
si sposta verso destra e Y aumenta. Se le politiche sono
restrittive e, pertanto, fanno diminuire Y, la AD si sposta
verso il basso e verso sinistra
Politica fiscale restrittiva: un aumento di T o
riduzione di G.
i
Un aumento di T
sposta la IS verso
il basso in IS’
LM(P0)
IS’
Y1
P
P0
A’
IS
A
AD’
Y0
Y
Y0
Y0
AD
Y
Offerta aggregata di breve e medio periodo
• La funzione dell’offerta aggregata (AS) mostra il valore dei
beni e servizi che le imprese di un sistema economico
desiderano offrire ai vari livelli dei prezzi.
• Per semplicità la AS indica, per ogni dato livello di P,
quale è la quantità prodotta, aggregando tutti i costi
marginali di tutte le imprese sul mercato. Cm = w/PML
• In un mondo in cui i prezzi non variano (keynesiano) nel
breve periodo, la AS è orizzontale. Variazione della AD
comportano una variazione del reddito.
• In un mondo in cui ci sono rigidità dei prezzi nel medio
periodo, la AS è crescente, quindi variazioni della AD
comporta sia un aumento del reddito, sia dei prezzi.
Modello AD AS
• Il modello macroeconomico imperniato sulla combinazione della
curva della domanda aggregata e della curva di offerta aggregata è
noto come modello AD-AS.
• Mentre P è una variabile endogena del modello.
• Il modello AD-AS ci permette di calcolare: (i) il livello
dell’occupazione; (ii) il livello del salario reale; (iii) il livello e la natura
della disoccupazione, oltre che il livello dei prezzi.
• Fig. 25.2 del libro. All’equilibrio della AD AS corrisponde un tasso di
disoccupazione, in quanto il salario reale più alto di quello di pieno
impiego. Ad un equilibrio del mercato del lavoro, piena occupazione
delle risorse, corrisponde un prodotto potenziale e quindi, un gap di
produzione.
• Per ridurre disoccupazione, occorre attuare politiche AS (riduzione
salari) e AD (fiscali, monetarie espansive a costo di inflazione
maggiore).
15
L’equazione dei salari
• Assumiamo che l’interazione tra lavoratori e imprese nella
negoziazione dei contratti di lavoro stabilisca la seguente
equazione dei salari nominali (W):
W = P F (u , z )
e
W aumenta in modo esattamente proporzionale alle
aspettative di prezzo Pe per conservare il potere di
acquisto atteso.
Per ora semplifichiamo e si assume Pe =P
L’equazione dei salari
W = PF ( u , z )
W aumenta se il tasso di disoccupazione u diminuisce
poiché aumenta il potere dei lavoratori:
– Alle imprese conviene pagare salari più elevati per non
perdere i lavoratori migliori (ipotesi salari di efficienza).
z è l’indicatore delle condizioni strutturali del mercato del
lavoro (es. sussidi di disoccupazione, forte presenza
sindacale, livello della contrattazione dei w).
W aumenta se i sindacati hanno un potere maggiore nella
contrattazione collettiva (z alto).
L’equazione dei prezzi
Funzione di produzione aggregata: Y=f(N). La produttività
marginale del lavoro è funzione decrescente della
produzione. P=w/PML. Se Y PML e P .
In concorrenza perfetta, l’equilibrio per le imprese sul
mercato del lavoro è Cm=w/PML; se la PML è pari a 1,
siccome in equilibrio P=Cm, allora P=w.
Ma se vige concorrenza imperfetta, allora il potere di
monopolistico delle imprese è espresso dal mark-up (µ).
Tanto maggiore il grado di concorrenza nel mercato dei
beni, tanto minore è µ. P>Cm; quindi, P > w
Allora, i prezzi sono dati dalla seguente equazione:
P = (1 + µ )W
Forme di mercato
(monopolio)
Monopolio e concorrenza
19
(1) In concorrenza il prezzo è uguale al costo marginale ; in
monopolio è maggiore: si ha infatti p > Rm = Cm.
Lo scarto tra prezzo e costo marginale misura il grado di
monopolio. Usiamo per quest’ultimo il simbolo µ; abbiamo allora
µ = (p − Cm)/p (una percentuale).
(2) In concorrenza gli extraprofitti sono destinati ad annullarsi
nel lungo periodo; in monopolio no (perché le barriere
impediscono l’ingresso delle altre imprese).
Gli extraprofitti in concorrenza sono “quasi-rendite”
(temporanee); in monopolio sono “rendite” (permanenti).
Corso di economia politica
Il tasso naturale di disoccupazione
Salario reale,
W/P
Equazione dei prezzi PS
1/(1+µ)
Equazione dei salari WS
un
Tasso di disocupazione, u
un = disoccupazione di equilibrio quando P=Pe
Disoccupazione e inflazione
• Il tasso naturale di disoccupazione dipende da alcune
caratteristiche del mercato del lavoro e del mercato dei
µ + z
prodotti. In particolare:
un =
α
z: la forza contrattuale dei sindacati, il livello del salario
minimo, le protezioni del mercato del lavoro (tra cui i sussidi di
disoccupazione)
α: la reattività dei salari al tasso di disoccupazione
μ: il grado di concorrenza nel mercato dei prodotti
NOTA: il tasso naturale di disoccupazione può cambiare al mutare
delle condizioni strutturali rappresentate da μ, z e α
Statica comparata: variazioni in μ, z e α muovono le curve WS e PS e
comportano variazioni in un.